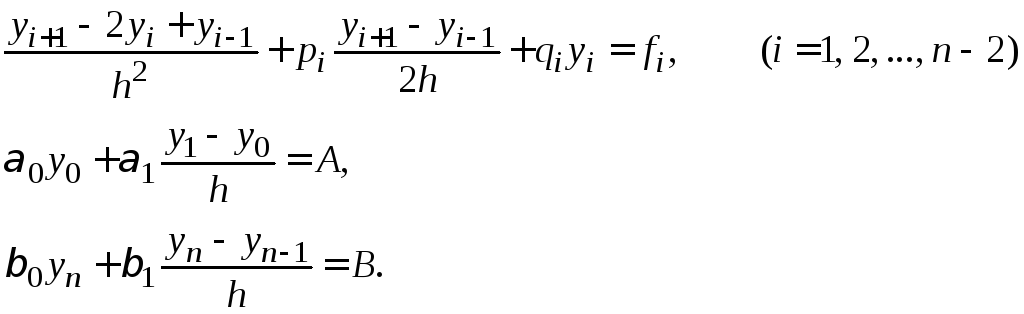- •Математическое моделирование и вычислительный эксперимент.
- •Виды погрешностей.
- •2. Приближенное решение нелинейных уравнений
- •3.Численное решение систем нелинейных уравнений.
- •4.Численные методы решения систем линейных алгебраических уравнений (слау).
- •5. Численное интегрирование. Квадратурные формулы Ньютона–Котеса. Формула трапеций, формула Симпсона. Погрешность квадратурных формул. Интегрирование с помощью степенных рядов. Метод Монте-Карло.
- •6. Численное дифференцирование.
- •7. Интерполирование функций.
- •8. Численное решение задачи Коши для дифференциальных уравнений.
- •9. Краевые задачи для обыкновенных дифференциальных уравнений.
- •13. Комбинаторные объекты и комбинаторные числа
- •14. Рекуррентные соотношения
- •15. Булевы функции. Представление булевых функций полиномами Жегалкина.
- •17. Множества.
- •Операции над множествами
- •Свойства отношений
- •Примеры отношений эквивалентности
- •18. Графы.
- •Эйлеровы графы.
- •5 Красок
- •19. Алгоритмы на графах. Алгоритмы на графах.
- •Задача о кратчайших путях
- •Различные алгоритмы на графах
- •Перебор с возвратами
- •Методы сокращения перебора: эвристики, метод ветвей и границ, динамическое программирование.
- •20. Деревья.
- •21. Проблема разрешимости в алгебре высказываний.
- •24. Понятие о компьютерном математическом моделировании. Этапы и цели. Классификация математических моделей. Моделирование физических процессов.
- •25. Имитационное моделирование.
- •26. Моделирование фрактальных объектов. Моделирование фрактальных объектов.
- •Самоподобные множества с необычными свойствами в математике
- •Рекурсивная процедура получения фрактальных кривых
- •Фракталы как неподвижные точки сжимающих отображений
- •Фракталы в комплексной динамике
- •Стохастические фракталы
- •Применение фракталов
- •Конструктивные, алгебраические и стохастические фракталы.
- •Понятие о фрактальной размерности.
- •Рекурсивный алгоритм построения конструктивных фракталов.
- •Построение
- •Свойства
9. Краевые задачи для обыкновенных дифференциальных уравнений.
Постановка краевой задачи для обыкновенного дифференциального уравнения
Пусть дано дифференциальное уравнение второго порядка
|
|
(1.10) |
Двухточечная краевая задача для уравнения (1.10) ставится следующим образом.
Найти
функцию
![]() ,
которая внутри отрезка
,
которая внутри отрезка![]() удовлетворяет
уравнению (110), а на концах отрезка —
краевым условиям
удовлетворяет
уравнению (110), а на концах отрезка —
краевым условиям
|
|
(1.11) |
Рассмотрим случай, когда уравнение (1.10) и граничные условия (1.11) линейны. В этом случае дифференциальное уравнение и краевые условия записываются так:
|
|
(1.12) |
|
|
(1.13) |
где
![]() –
известные непрерывные на отрезке
–
известные непрерывные на отрезке![]() функции,
функции,![]() –
заданные постоянные, причем
–
заданные постоянные, причем![]() и
и![]() .
.
Приближенное решение обыкновенных дифференциальных уравнений методом конечных разностей
Данный метод заключается в следующем.
Разбиваем
отрезок
![]() наn
равных частей с шагом
наn
равных частей с шагом
![]() и получаем точки
и получаем точки![]() ,
в которых требуется найти искомые
значения
,
в которых требуется найти искомые
значения![]() .
.
Введем
обозначения:
![]()
Заменим
приближенно в каждом внутреннем узле
производные
![]() конечно-разностными схемами:
конечно-разностными схемами:
|
|
(1.14) |
а на концах отрезка положим:
|
|
(1.15) |
Используя формулы (1.14)–(1.15), приближенно заменим уравнения (1.12)-(1.13) системой уравнений:
|
|
(1.16) |
Получим линейную алгебраическую систему, содержащую n+1 уравнение с n+1 неизвестным. Решив данную систему, получаем таблицу приближенных значений искомой функции.
Более
точные формулы получаются, если заменить
![]() центрально-разностными отношениями:
центрально-разностными отношениями:
|
|
(1.17) |
а на концах отрезка положить:
|
|
(1.18) |
Используя эти формулы, приближенно заменим уравнения (1.12)–(1.13) системой уравнений:
|
|
(1.19) |
Приближенное решение обыкновенных дифференциальных уравнений методом прогонки
При большом n непосредственное решение системы (1.16) становится громоздким. Поэтому были разработаны различные методы решения систем такого вида, например, метод прогонки.
Рассмотрим систему (1.16). Метод прогонки решения системы заключается в следующем.
Запишем
уравнения системы (1.14) в виде:![]() ,
где
,
где
|
|
(1.23) |
Полученную систему приводим к виду:
|
|
(1.24) |
Числа
![]() последовательно вычисляются по формулам:
последовательно вычисляются по формулам:
при
![]()
|
|
(1.25) |
При
![]()
|
|
(1.26) |
Вычисления производятся в следующем порядке.
Прямой
ход. По
формулам (1.23) вычисляем значения
![]() .
Находим
.
Находим![]() по формулам (1.25). Затем вычисляем
по формулам (1.25). Затем вычисляем![]() по формулам (1.26) для
по формулам (1.26) для![]()
Обратный
ход. Из
уравнения (1.24) при
![]() и последнего уравнения системы (1.16)
получаем:
и последнего уравнения системы (1.16)
получаем:
![]()
Решив
эту систему относительно
![]() ,
будем иметь
,
будем иметь
|
|
(1.27) |
Используя
уже известные числа
![]() ,
находим
,
находим![]() .
Затем вычисляем значения
.
Затем вычисляем значения![]() ,
последовательно применяя рекуррентные
формулы (1.22):
,
последовательно применяя рекуррентные
формулы (1.22):
|
|
(1.28) |
Значение
![]() находим из предпоследнего уравнения
системы (1.16):
находим из предпоследнего уравнения
системы (1.16):
|
|
(1.29) |
Таким образом, все вычисления «прогоняются» два раза.
Вычисления
прямого хода заготавливают вспомогательные
числа
![]() в порядке возрастания индекса
в порядке возрастания индекса![]() .
При этом для вычисления значений
.
При этом для вычисления значений![]() используется краевое условие на левом
конце отрезка интегрирования. Затем на
первом шаге обратного хода происходит
согласование полученных чисел
используется краевое условие на левом
конце отрезка интегрирования. Затем на
первом шаге обратного хода происходит
согласование полученных чисел![]() с краевым условием на правом конце
отрезка интегрирования, после чего
последовательно получаются значения
искомой функции
с краевым условием на правом конце
отрезка интегрирования, после чего
последовательно получаются значения
искомой функции![]() в порядке убывания индекса
в порядке убывания индекса![]() .
.