
- •Математическое моделирование и вычислительный эксперимент.
- •Виды погрешностей.
- •2. Приближенное решение нелинейных уравнений
- •3.Численное решение систем нелинейных уравнений.
- •4.Численные методы решения систем линейных алгебраических уравнений (слау).
- •5. Численное интегрирование. Квадратурные формулы Ньютона–Котеса. Формула трапеций, формула Симпсона. Погрешность квадратурных формул. Интегрирование с помощью степенных рядов. Метод Монте-Карло.
- •6. Численное дифференцирование.
- •7. Интерполирование функций.
- •8. Численное решение задачи Коши для дифференциальных уравнений.
- •9. Краевые задачи для обыкновенных дифференциальных уравнений.
- •13. Комбинаторные объекты и комбинаторные числа
- •14. Рекуррентные соотношения
- •15. Булевы функции. Представление булевых функций полиномами Жегалкина.
- •17. Множества.
- •Операции над множествами
- •Свойства отношений
- •Примеры отношений эквивалентности
- •18. Графы.
- •Эйлеровы графы.
- •5 Красок
- •19. Алгоритмы на графах. Алгоритмы на графах.
- •Задача о кратчайших путях
- •Различные алгоритмы на графах
- •Перебор с возвратами
- •Методы сокращения перебора: эвристики, метод ветвей и границ, динамическое программирование.
- •20. Деревья.
- •21. Проблема разрешимости в алгебре высказываний.
- •24. Понятие о компьютерном математическом моделировании. Этапы и цели. Классификация математических моделей. Моделирование физических процессов.
- •25. Имитационное моделирование.
- •26. Моделирование фрактальных объектов. Моделирование фрактальных объектов.
- •Самоподобные множества с необычными свойствами в математике
- •Рекурсивная процедура получения фрактальных кривых
- •Фракталы как неподвижные точки сжимающих отображений
- •Фракталы в комплексной динамике
- •Стохастические фракталы
- •Применение фракталов
- •Конструктивные, алгебраические и стохастические фракталы.
- •Понятие о фрактальной размерности.
- •Рекурсивный алгоритм построения конструктивных фракталов.
- •Построение
- •Свойства
3.Численное решение систем нелинейных уравнений.
Метод Ньютона для систем нелинейных уравнений.
Пусть дана система:
![]()
Согласно методу Ньютона последовательные приближения вычисляются по формулам:
![]() ,
где
,
где
![]()
![]()
Начальные
приближения
![]() определяются приближенно (например,
графически).
определяются приближенно (например,
графически).
Метод Ньютона эффективен только при достаточной близости начального приближения к решению системы.
4.Численные методы решения систем линейных алгебраических уравнений (слау).
Метод Гаусса с выбором главного элемента для системы линейных уравнений
Система из п линейных уравнений с п неизвестными вида:
 (3.1)
(3.1)
имеет
единственное решение при условии:
![]()
![]() ,
где
,
где

матрица коэффициентов
матрица коэффициентов
![]() системы (3.1)
системы (3.1)
К
точным методам относится метод Гаусса
с выбором главного элемента. Среди
элементов
![]() матрицыА
выберем наибольший по модулю, называемый
главным
элементом.
Пусть им будет элемент
матрицыА
выберем наибольший по модулю, называемый
главным
элементом.
Пусть им будет элемент
![]() .
Строка с номеромр,
содержащая главный элемент, называется
главной строкой.
.
Строка с номеромр,
содержащая главный элемент, называется
главной строкой.
Далее
вычисляем множители:
![]() для всех
для всех![]() .
Затем преобразуем матрицу следующим
образом: из каждой неглавной строки
вычитаем почленно главную строку,
умноженную наmi
. В результате получим матрицу, у которой
все элементы q-го
столбца, за исключением
.
Затем преобразуем матрицу следующим
образом: из каждой неглавной строки
вычитаем почленно главную строку,
умноженную наmi
. В результате получим матрицу, у которой
все элементы q-го
столбца, за исключением
![]() ,
равны нулю. Отбрасываем этот столбец и
главную строку и
,
равны нулю. Отбрасываем этот столбец и
главную строку и
получаем
новую матрицу
![]() с меньшим на единицу числом строк и
столбцов. Над матрицей
с меньшим на единицу числом строк и
столбцов. Над матрицей![]() повторяем аналогичные операции, после
чего получаем матрицуА2
и т. д. Такие преобразования продолжаем
до тех пор, пока не получим матрицу,
содержащую одну строку, которую считаем
тоже главной. Затем объединяем все
главные строки, начиная с последней.
После некоторой перестановки они
образуют треугольную матрицу, эквивалентную
исходной. На этом заканчивается этап
вычислений, называемый прямым
ходом. Решив
систему с полученной треугольной
матрицей коэффициентов, найдём
последовательно значения неизвестных
повторяем аналогичные операции, после
чего получаем матрицуА2
и т. д. Такие преобразования продолжаем
до тех пор, пока не получим матрицу,
содержащую одну строку, которую считаем
тоже главной. Затем объединяем все
главные строки, начиная с последней.
После некоторой перестановки они
образуют треугольную матрицу, эквивалентную
исходной. На этом заканчивается этап
вычислений, называемый прямым
ходом. Решив
систему с полученной треугольной
матрицей коэффициентов, найдём
последовательно значения неизвестных
![]() .
Этот этап вычислений называетсяобратным
ходом. Смысл
выбора главного элемента состоит в том,
чтобы сделать достаточно малым число
mi
и тем самым уменьшить погрешность
вычислений.
.
Этот этап вычислений называетсяобратным
ходом. Смысл
выбора главного элемента состоит в том,
чтобы сделать достаточно малым число
mi
и тем самым уменьшить погрешность
вычислений.
Вычисление обратной матрицы для системы линейных уравнений
Пусть
дана невырожденная матрица
![]() ,
где(i,
j
= 1, 2,…, n).
Для нахождения элементов обратной
матрицы
,
где(i,
j
= 1, 2,…, n).
Для нахождения элементов обратной
матрицы
![]() ,
где (i,
j
= 1, 2,… n)
воспользуемся основным соотношением:
,
где (i,
j
= 1, 2,… n)
воспользуемся основным соотношением:
АА-1 =Е, где Е – единичная матрица.
Перемножая
матрицы А
и А-1
и используя
равенство их матрице Е,
получим п
систем линейных уравнений вида:![]() (i
= 1, 2, …,
n;
j
– фиксировано),
где
(i
= 1, 2, …,
n;
j
– фиксировано),
где
![]() .
.
Полученные п систем линейных уравнений имеют одну и ту же матрицу А и различные столбцы свободных членов. Эти системы можно решать методом Гаусса (см. п. 3.1.1). В результате решения систем получаем единичную матрицу A.
Метод простой итерации для систем линейных уравнений
Метод простой итерации даёт возможность получить последовательность приближённых значений, сходящуюся к точному решению системы.
Преобразуем систему (3.1) к нормальному виду:
![]() . (3.2)
. (3.2)
Правая часть системы (3.2) определяет отображение:
![]() ,
преобразующее точку
,
преобразующее точку
![]() -мерного
-мерного
метрического
пространства в точку
![]() того же пространства.
того же пространства.
Выбрав
начальную точку ![]() ,
можно построить итерационную
последовательность точекп
- мерного пространства:
,
можно построить итерационную
последовательность точекп
- мерного пространства:
![]()
При определённых условиях данная последовательность сходится.
Так, для исследования сходимости таких последовательностей используется принцип сжимающих отображений, который состоит в следующем.
Если
F
– сжимающее
отображение, определённое в полном
метрическом пространстве с метрикой
![]() ,
то существует единственная неподвижная
точка
,
то существует единственная неподвижная
точка![]() ,
такая, что
,
такая, что![]() .
При этом итерационная последовательность,
.
При этом итерационная последовательность,![]() ,
полученная с помощью отображенияF
с любым начальным членом х(0),
сходится к
,
полученная с помощью отображенияF
с любым начальным членом х(0),
сходится к
![]() .
.
Оценка
расстояния между неподвижной точкой
![]() отображенияF
и приближением
х(к)
даётся формулами:
отображенияF
и приближением
х(к)
даётся формулами:
 (3.3)
(3.3)
где α – множитель, определяемый достаточными условиями сжимаемости отображения F.
Значение
множителя α,
определяется выбором метрики, в которой
проверяется сходимость последовательности
значений
![]() .
.
Рассмотрим
Достаточные условия сходимости
итерационной последовательности
![]() .
.
Практически, для применения метода итерации систему линейных уравнений удобно "погрузить" в одну из трёх следующих метрик:
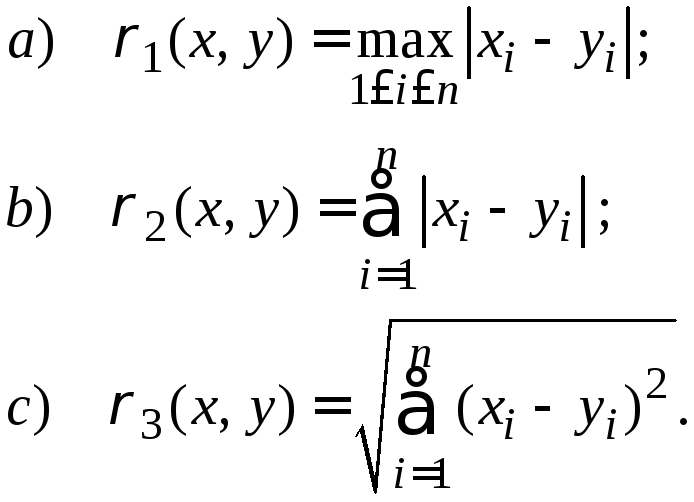 (3.4)
(3.4)
Для того, чтобы отображение F, заданное в метрическом пространстве соотношениями (3.2), было сжимающим, достаточно выполнение одного из следующих условий:
а)
в пространстве с метрикой
![]() :
:
![]() ,
т. е. максимальная из сумм модулей
коэффициентов в правой части системы
(3.2), взятых по строкам, должна быть меньше
единицы.
,
т. е. максимальная из сумм модулей
коэффициентов в правой части системы
(3.2), взятых по строкам, должна быть меньше
единицы.
б) в
пространстве с метрикой
![]() :
:![]() ,
т. е. максимальная из сумм модулей
коэффициентов в правой части системы
(3.2), взятых по столбцам, должна быть
меньше единицы.
,
т. е. максимальная из сумм модулей
коэффициентов в правой части системы
(3.2), взятых по столбцам, должна быть
меньше единицы.
в) в
пространстве с метрикой
![]() :
:
![]() ,
т. е. сумма квадратов при неизвестных в
правой части системы (3.2) должна быть
меньше единицы
,
т. е. сумма квадратов при неизвестных в
правой части системы (3.2) должна быть
меньше единицы
Метод Зейделя для систем линейных уравнений
Метод
Зейделя является модификацией метода
простой итерации. Вычисление
![]() проводится по следующим формулам:
проводится по следующим формулам:

Достаточные условия сходимости итерационной последовательности приближенных решений системы и оценка погрешности проводятся по тем же формулам, что и в методе простой итерации.
