Chau Chemometrics From Basics to Wavelet Transform

Figure 5.43. An experimental photoacoustic spectrum (a) and its first- (b) and second-

(c) order derivatives calculated by CWT with a = 100 [From Fresenius J. Anal. Chem. 367:525--529 (2000)].

5.4.3.Comparison between Wavelet Transform and other

Numerical Differentiation Methods

Here, we compared the derivatives obtained using different methods, including numerical differentiation, the Fourier transform method, the Savitsky--Golay method, the DWT method, the DWT method with the improved WT algorithm, and the CWT method with a = 50. The firstorder derivatives of the above two simulated signals by these methods are shown in Figure 5.44, respectively. From the figure it can be seen that, for the signal without noise, all the results are almost the same. But for the noisy signal, only the last two methods can obtain smooth derivatives.

Table 5.4 lists the parameters describing these results in the left column of Figure 5.44. The definition of the peak width and peak position is depicted in Figure 5.44, curve (f). From the parameters in the table, we can find that all the methods give the same peak position, but the peak width is slightly different. Because it is difficult to determine the exact beginning and ending points of the peaks, there is a large error in the peak width in the table. But it is evident that the peak width in the results using the CWT method is comparatively greater than from the other methods.

Figure 5.44. Comparison of the first derivatives of the clean (left column) and noisy (right column) simulated signals calculated by numerical differentiation (a), Fourier transform method (b), Savitsky--Golay method (c), DWT method (d), DWT method with the improved WT algorithm (e), and the CWT method (f).

Table 5.4. Comparison of Peak Position and Width of Calculated Derivatives by Different Derivative Calculation Methods

212application of wavelet transform in chemistry

5.4.4.Resolution Enhancement

According to the characteristics of the WT, a signal can be decomposed into its contributions by the MRSD method to obtain discrete details dj and discrete approximations cj , which represent the different components of the signal at different frequencies. If an overlapping or low-resolution signal is decomposed into its contributions, there must be discrete details that represent the information at the frequency lower than noise and higher than the original signal. Therefore, it is not difficult to select a detail at medium scale to obtain the high-resolution information of the signal. Furthermore, if we amplify one or several of these selected details and then perform the inverse transform, that is, reconstruct the original signal with the amplified contributions, we can also obtain a signal with high resolution.

Therefore, there are generally two methods using WT for resolution enhancement of analytical signals:

1.Decompose the analyzing signal c0 into its approximations cj and details dj using Equations (5.32) and (5.33).

2.Inspect the cj and dj , then select either (a) a detail component as the resolved result for further studies (method A), or (b) one or more detail components that represent the high-resolution information of the analyzing signal (method B).

3.Multiply the selected dj by a factor k whose value is bigger than 1.0 and reconstruct the signal by using Equation (5.34) (method B).

Example 5.12: Resolution Enhancement of an Overlapping Chromatogram Using Method A. Curve (c0) in Figure 5.45 is an experimental chromatogram, and curves (d4), (d5), and (d6) are its detail components obtained by using the improved WT algorithm in Equations (5.32) and (5.33) with Symmlet (L = 4) wavelet at scale parameter j = 4, 5, and 6, respectively.

As discussed in the WT denoising section, the frequency of the detail components dj obtained by a WT decomposition decreases with the increase of the scale parameter j . The detail components at low scales are generally composed of noise. From Figure 5.45, it is clear that d4 is still composed mainly of noise, but d5 and d6 are composed of chromatographic information whose frequency is higher than that of noise and lower than that of the original signal. That is to say, the d5 and d6 are the desired highresolution part of the analytical signal. Therefore, in the detail components on medium scale, we can find one or more components which represent the high-resolution information of the analytical signal. If we further compare d5 and d6, it is easy to find that d5 is the better one for representing

Figure 5.45. An experimental chromatogram (c0) and its detail components obtained by WT with j = 4(d4), 5(d5), and 6(d6).

the high-resolution information, which can be used for further studies, such as determination of peak position and quantitative calculation.

Computational Details of Example 5.12

1.Load the experimental chromatogram [Fig. 5.45 (c0)].

2.Extend the chromatographic data for avoiding the edge effect.

3.Make a wavelet filter---Symmlet4.

4.Set resolution level J = 6.

5.Perform WT to obtain the c and d components with the improved algorithm.

6.Display Figure 5.45.

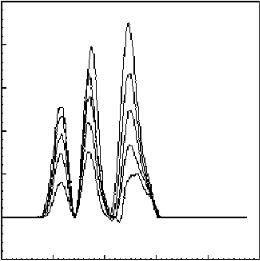
Because this method can extract the high-resolution information from a low-resolution or overlapping analytical signal, a method for determination of the component number in overlapping chromatograms was proposed. Figure 5.46 shows four experimental chromatograms with different intensities. It is impossible to obtain the correct component number from such chromatograms. Figure 5.47 shows the d5 component of the four chromatograms in Figure 5.46 obtained with Symmlet wavelet filters (L = 4). The dotted line in the figure indicates the position of zero in the magnitude axis. From Figure 5.47, it is clear that there are five components in the chromatograms, and all four chromatograms of different magnitude give us the same result.

Figure 5.46. Four experimental chromatograms with different amplitudes [from Chemometr. Intell. Lab. Syst. 43:147--155 (1998)].

Because the WT is a linear transform, the high-resolution information should be used for quantitative calculation. An example of quantitative determination of the components in overlapping chromatographic peaks was published in Analytical Chemistry, [69:1722--1725 (1997)]. Figure 5.48 shows the chromatograms of five mixed samples of benzene, methyl benzene, and ethyl benzene. It is difficult to perform quantitative calculation

Figure 5.47. The detail component d5 obtained from the four chromatograms in Figure 5.46 by WT decomposition [from Chemometr. Intell. Lab. Syst. 43:147--155 (1998)].