Контрольные вопросы
В каких случаях возникает необходимость использовать Таблицу подстановок?
Каким образом необходимо выстроить данные для того, чтобы воспользоваться таблицей подстановок?
В какой ячейке рабочего листа записывается расчетная формула при проведении вычислений с помощью таблицы подстановок?
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ ПО ТЕМЕ 7
Задача 1.
Задание. Государство стремится увеличить налоги, чтобы пополнить бюджет для выполнения социально-экономических и оборонных функций. Налогоплательщики в свою очередь не могут обеспечить выживание бизнеса при непомерном росте налогов. Определите оптимальное сочетание уровня рентабельности и налоговой ставки, при котором поступления в бюджет будут максимальными. На основе полученных данных постройте график, отображающий зависимость поступлений в бюджет от ставки налога и уровня рентабельности.
Примечания. Прибыль предприятия зависит от его рентабельности и определяется как произведение капитала на процент рентабельности (таблица 3 на рисунке 1.54).
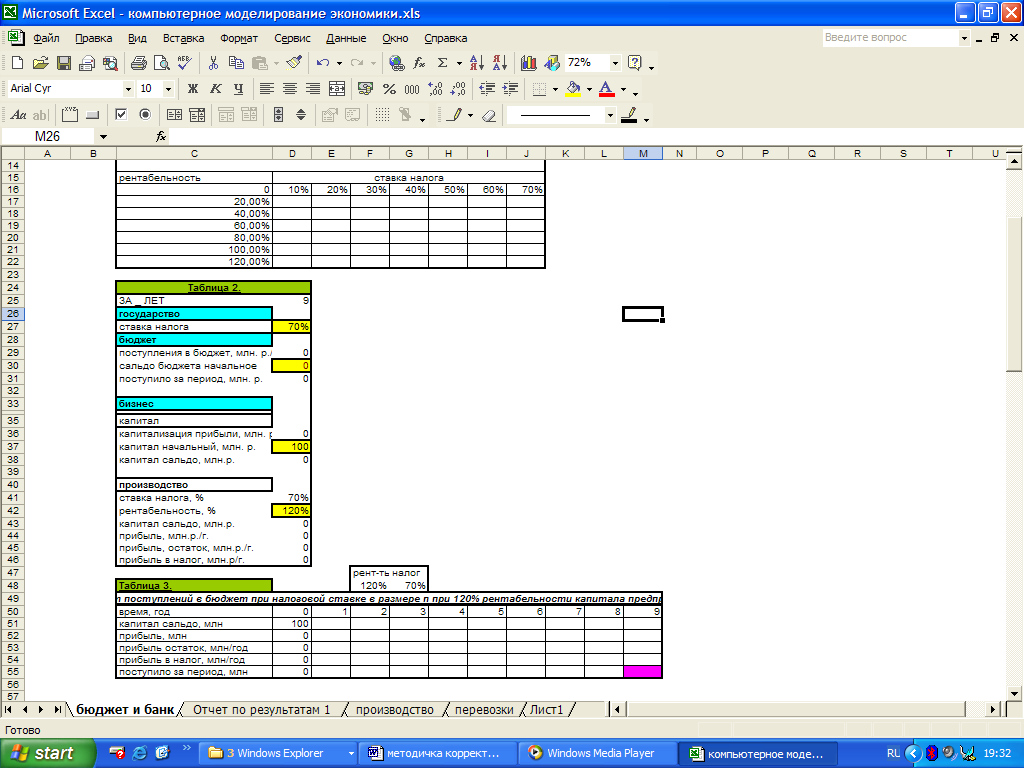
Рис 1.54. Расчет поступлений в бюджет
Прибыль, идущая в качестве налога в бюджет, равна произведению суммы прибыли на налоговую процентную ставку. Остаток прибыли - это прибыль, оставшаяся после уплаты налога. Капитал сальдо определяется путем суммирования капитала за прошлый период и прибыли, оставшейся после уплаты налога за фактический период. Аналогичным образом определяется сумма поступлений в бюджет в последующие периоды. В таблице 1 необходимо получить суммы налоговых поступлений в бюджет при различных налоговых ставках и различном уровне рентабельности.
Задача 2.Создайте таблицу предполагаемых цен на основные продукты питания через 6, 12 и 18 месяцев (рис. 1.55). Инфляция составляет 10% в год. Цены на текущее число заданы. Цену товаров с учетом инфляции вычисляйте по формуле сложных процентов (функция БЗ). Расчет таблицы производите с помощью таблицы подстановок.
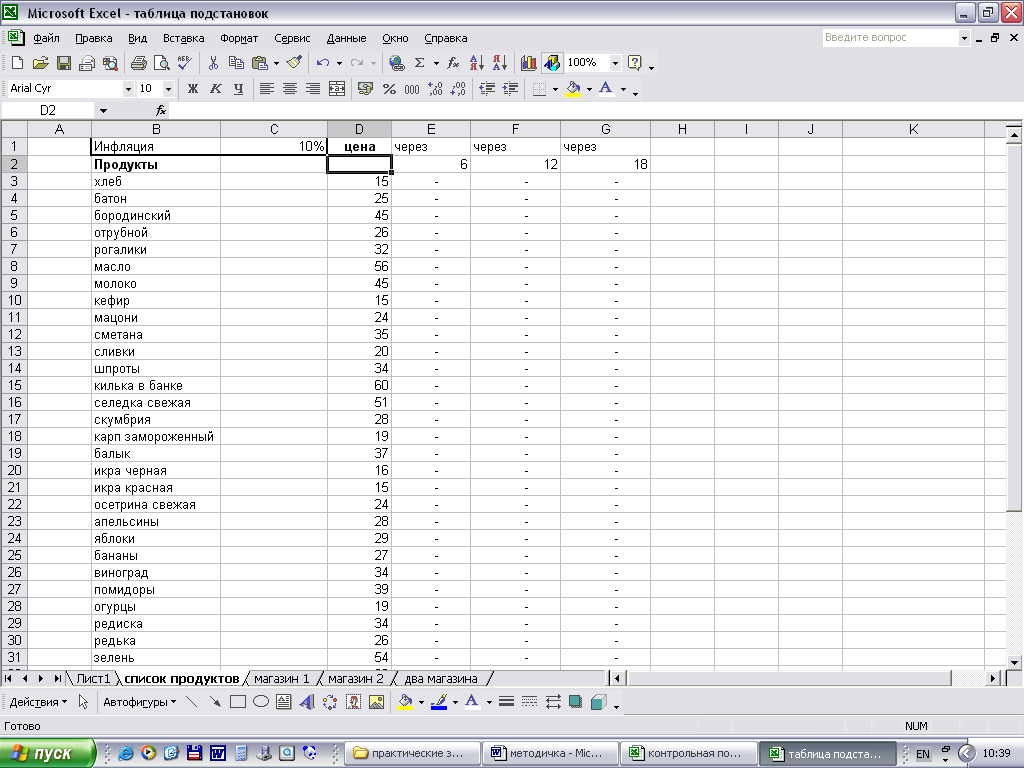
Рис. 1.55. Динамика цен на продукты питания
Тема 8. Программа оптимизации «поиск решения»
Цель работы: используя возможности программы Microsoft Excel эффективно планировать экономическую деятельность (решать задачи оптимизации).
Пример
Задание. Завод выпускает аудио- и видеотехнику. Известно, что на складе имеется запас комплектующих изделий в количестве указанном в таблице. Для производства каждого вида изделий требуются определенные затраты комплектующих. Каждому типу изделий соответствует своя норма прибыли. При увеличении объемов производства происходит уменьшение удельной прибыли в связи с дополнительными затратами на сбыт.
Составьте бизнес-план производства продукции таким образом, чтобы получить максимальную прибыль.
Исходные данные приведены в таблице на рисунке 1.56.
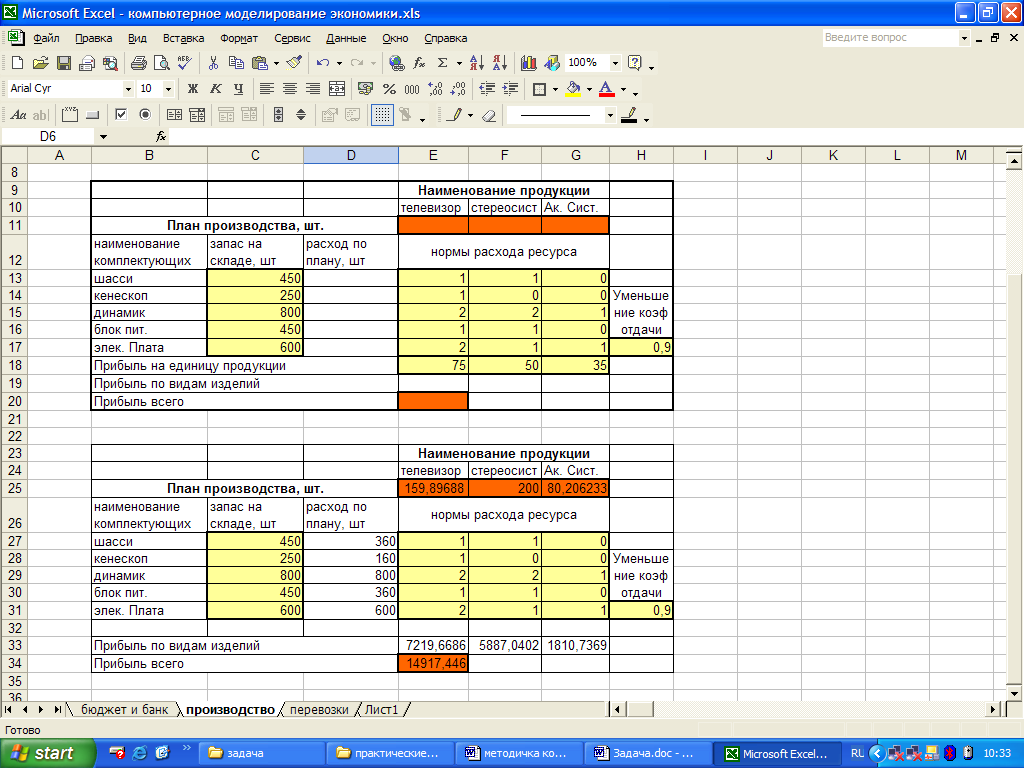
Рис. 1.56. Бизнес-план производства продукции
Решение. Создайте в приложении Microsoft Ехсеl таблицу, как показано на рис. 1.56. Заполните имеющимися данными.
Рассчитайте данные по столбцу «расход по плану». Для этого сложите произведения нормы расходов ресурсов по каждому наименованию продукции и плана производства этих видов продукции. Т.е. формула для ячейки D13 будет выглядеть следующим образом: =$E$11*E13+$F$11*F13+$G$11*G13. Остальные ячейки столбца заполните самостоятельно. В результате получите значение 0 во всех ячейках, т.к. ячейки Е11:G11 не содержат данных.
Теперь необходимо записать формулы для расчета прибыли по каждому виду изделий и прибыли всего. По видам изделий прибыль рассчитывается путем умножения прибыли на единицу изделия на максимально возможное количество произведенной продукции, скорректированное на уменьшение коэффициента отдачи. Для ячейки Е19 формула будет выглядеть следующим образом: 75*МАКС(Е11;0)^$Н$17.
Прибыль всего равна сумме прибыли по каждому виду изделий.
Таким образом, получили таблицу, содержащую данные, связанные формулами, но не показывающую результаты вычислений.
Для того, чтобы решить задачу, т.е. определить какое количество каждого вида изделия необходимо произвести, имея ограниченное число ресурсов, чтобы получить максимальную прибыль, необходимо использовать программу оптимизации Поиск решения.
Для вызова программы оптимизатора выберите команду меню Сервис, Поиск решения. Появилось Диалоговое окно Поиск решения. Поле Установить целевую ячейку служит для указания целевой ячейки, значение которой необходимо максимизировать, минимизировать или установить равным заданному числу. Эта ячейка должна содержать формулу. В данном примере это ячейка Е20.
Кнопка Равной служит для выбора варианта оптимизации значения целевой ячейки. В данном примере для максимизации прибыли нажмите кнопку Максимальному значению.
Поле Изменяя ячейки служит для указания ячеек, значения которых изменяются в процессе поиска решения до тех пор, пока не будут выполнены наложенные ограничения и условие оптимизации значения ячейки, указанном в поле Установить целевую ячейку. Изменяемые ячейки должны быть прямо или косвенно связаны с целевой ячейкой. Допускается установка до 200 изменяемых ячеек.
Поле Предположить используется для автоматического поиска ячеек, влияющих на формулу, ссылка на которую дана в поле установить целевую ячейку. Результат поиска отображается в поле Изменяя ячейки.
Поле Ограничения служит для отображения списка условий поставленной задачи. Заполните поле Ограничения как показано на рисунке 1.57. Неравенство $D$13:$D$17<=$C$13:$C$17 означает, что расход комплектующих на производство не может превышать запасы комплектующих на складе, $Е$11:$G$11>=0 значит, что количество произведенной продукции не может быть меньше нуля.
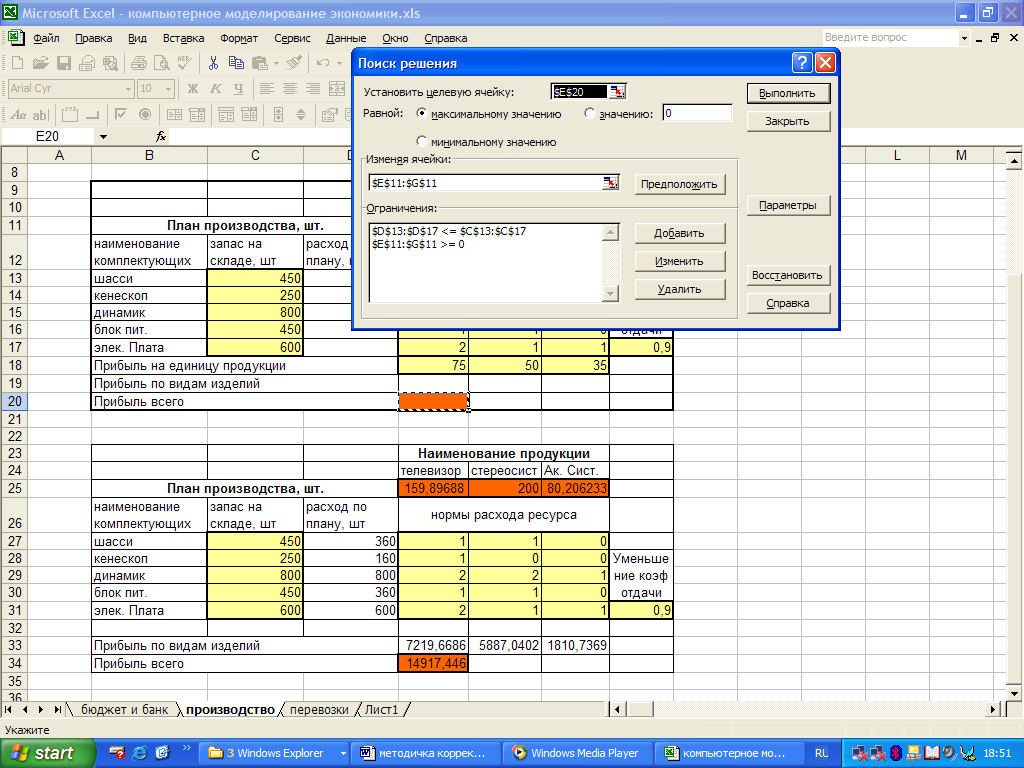
Рис. 1.57. Диалоговое окно программы Поиск решений
После того, как все необходимые условия оговорены нажмите Выполнить. В окне Результаты поиска решения нажмите ОК (рис. 1.58).
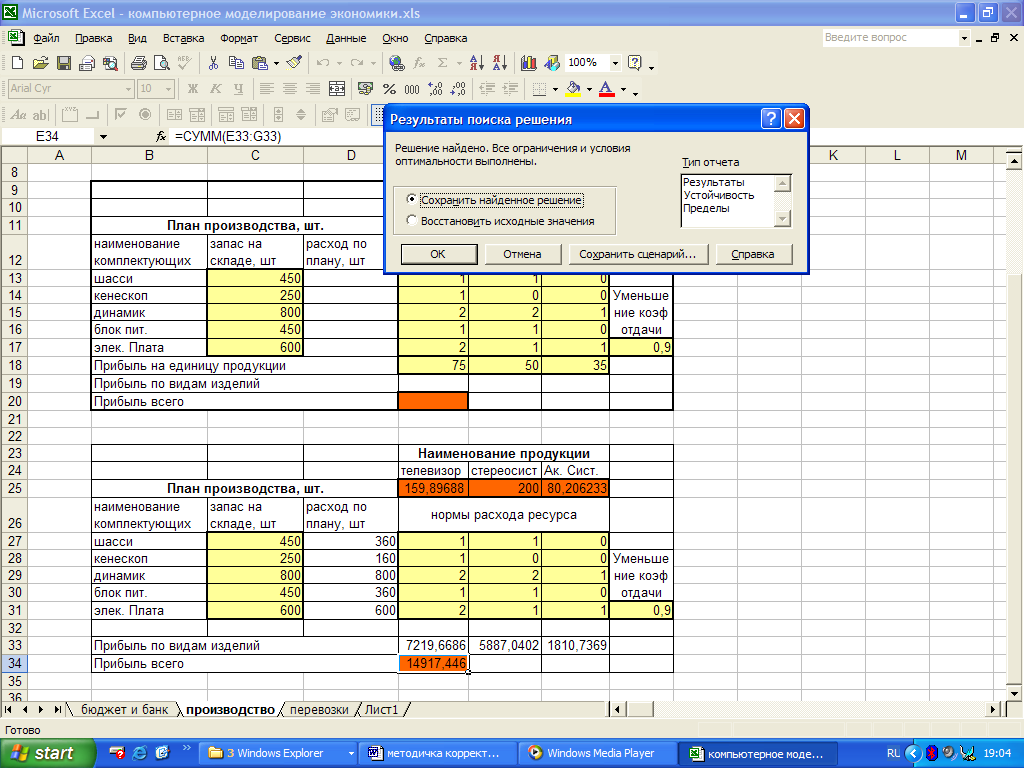
Рис. 1.58. Результаты поиска решений
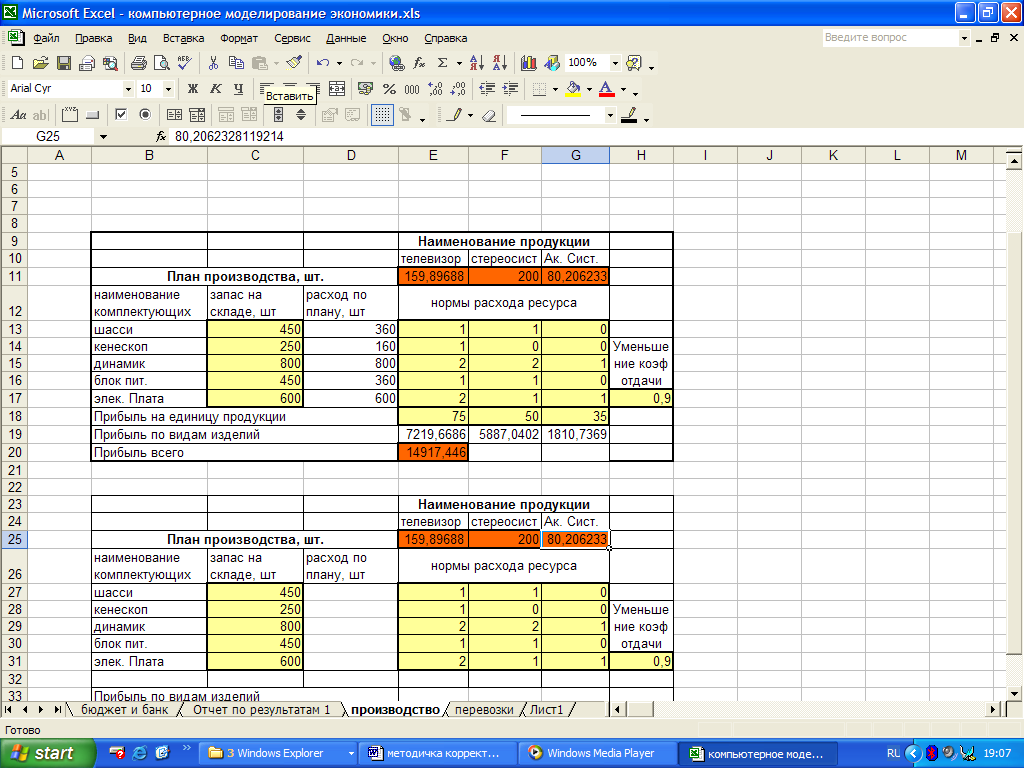
Рис. 1.59. Рассчитанный бизнес-план производства продукции
В таблице в пустых ячейках появились значения, показывающие, что для получения максимальной прибыли в размере 14 917 р. в условиях ограниченного количества ресурсов необходимо произвести 160 телевизоров, 200 стереосистем и 80 акустических систем, при этом максимально эффективно будут использованы имеющиеся на складе комплектующие (рис. 1.59).
Задание 2. Клиент банка имеет инвестиционный капитал и желает получить от него максимальную прибыль при минимальном риске потери средств. Необходимо сформировать оптимальный портфель акций клиента.
Решение. В однофакторной модели Шарпа доходность портфеля определяется по формуле Rp=Rf+(Rm-Rf)*Bp,
где Rp – доходность портфеля, %,
Rf – доходность безрисковых активов, %,
Rm – доходность рынка, %,
Bp – Бета портфеля – показатель системного, рыночного риска портфеля.
где Wi – доля актива I в портфеле,
Bi – Бета i-й акции,
i – номер бумаги в списке портфеля,
n – количество бумаг в портфеле.
Риск портфеля определяется дисперсией доходности портфеля:
где Vp – дисперсия доходности портфеля,
Vm - дисперсия доходности рынка,
Vi – дисперсия доходности i-й бумаги.
Исходными данными для расчета характеристик портфеля являются доходность безрисковых активов (Rf) = 6%, доходность рынка (Rm) = 15%, дисперсия (риск) доходности рынка (Vm) = 3%, Бета каждой акции (Bi) - акция А = 0,80, акция В = 1,00, акция С = 1,80, акция D = 2,20, казначейские векселя = 0,00, остаточная дисперсия каждой акции (Vi) - акция А = 0,04, акция В = 0,20, акция С = 0,12, акция D = 0,40, казначейские векселя = 0,00.
Необходимо максимизировать доходность портфеля при ограниченном риске (дисперсии доходности портфеля):
Rp → max,
Vp <= Vb,
,
Wi >= 0,
где Vb – заданное инвестором ограничение риска портфеля в долях или процентах.
Минимизировать риск при заданном ограничении уровня доходности портфеля:
Vp → min,
Rp <= Rb,
,
Wi >= 0,
где Rb – заданное инвестором ограничение по уровню доходности портфеля в долях или процентах.
Все необходимые для решения формулы представлены в таблице на рисунке 1.60.
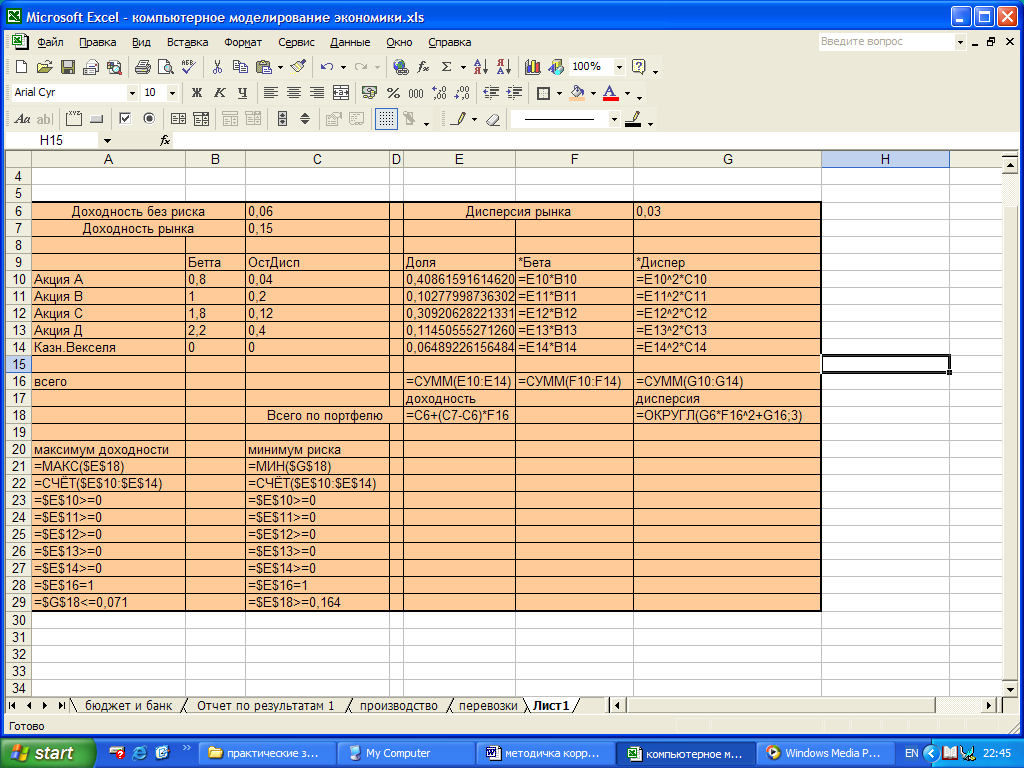
Рис. 1.60. Исходные данные для формирования эффективного портфеля ценных бумаг
Создайте аналогичную таблицу в приложении Microsoft Excel. Попытайтесь решить задачу вручную, подставляя значения в столбец Доля. Решение таким способом займет много времени.
Решите задачу с использованием команды Поиск решения. Для этого вызовите команду МЕНЮ СЕРВИС – ПОИСК РЕШЕНИЯ. В появившемся диалоговом окне оптимизатора заполните все необходимые поля (рис. 1.61).
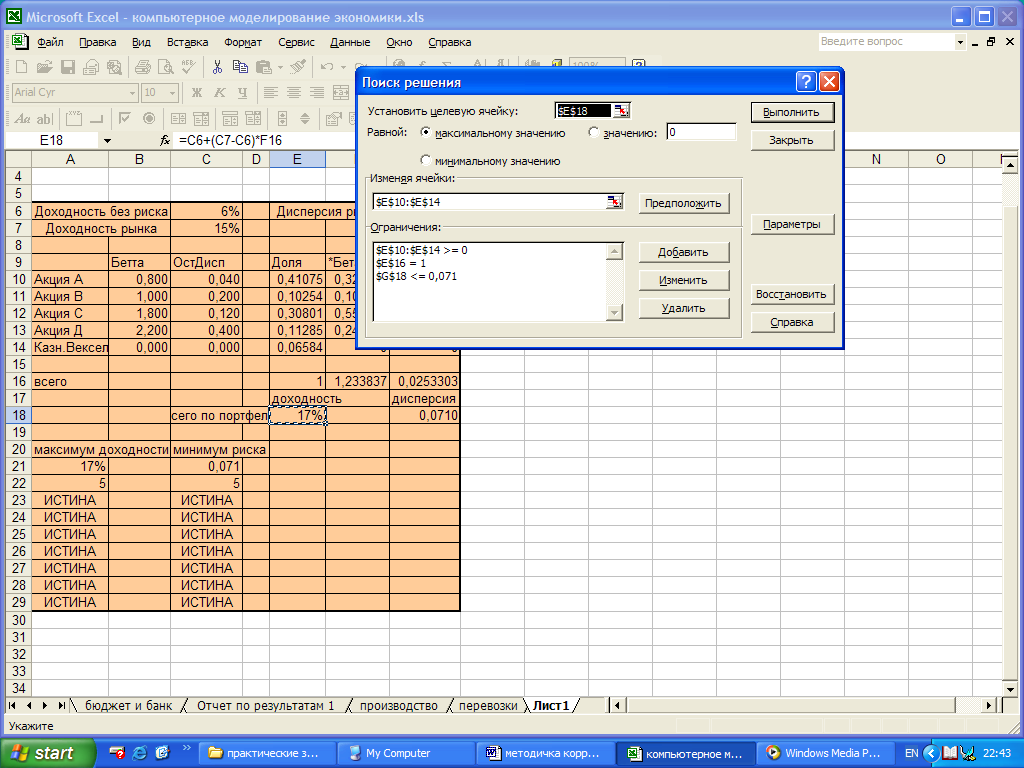
Рис. 1.61. Диалоговое окно программы Поиск решения
Нажмите ВЫПОЛНИТЬ, СОХРАНИТЬ НАЙДЕННОЕ РЕШЕНИЕ, ОК.
Рис. 1.62. Рассчитанная таблица
В результате получили структуру портфеля ценных бумаг, при которой в условиях ограничения процента риска на уровне не более 7,1% процент доходности максимальный – 17% (рис. 1.62).
Теперь определите структуру портфеля, при которой в условиях ограничения доходности не ниже 16,4% риск будет наименьшим. Для этого вызовите команду ПОИСК РЕШЕНИЯ. Далее можно как в прошлом случае заполнить поля вручную, но можно воспользоваться заданной моделью. В окне поиск решения нажмите кнопку ПАРАМЕТРЫ. В новом окне – ЗАГРУЗИТЬ МОДЕЛЬ.
Рис. 1.63. Окно Загрузка модели
Укажите область $С$21:$C$29. ОК, ОК.
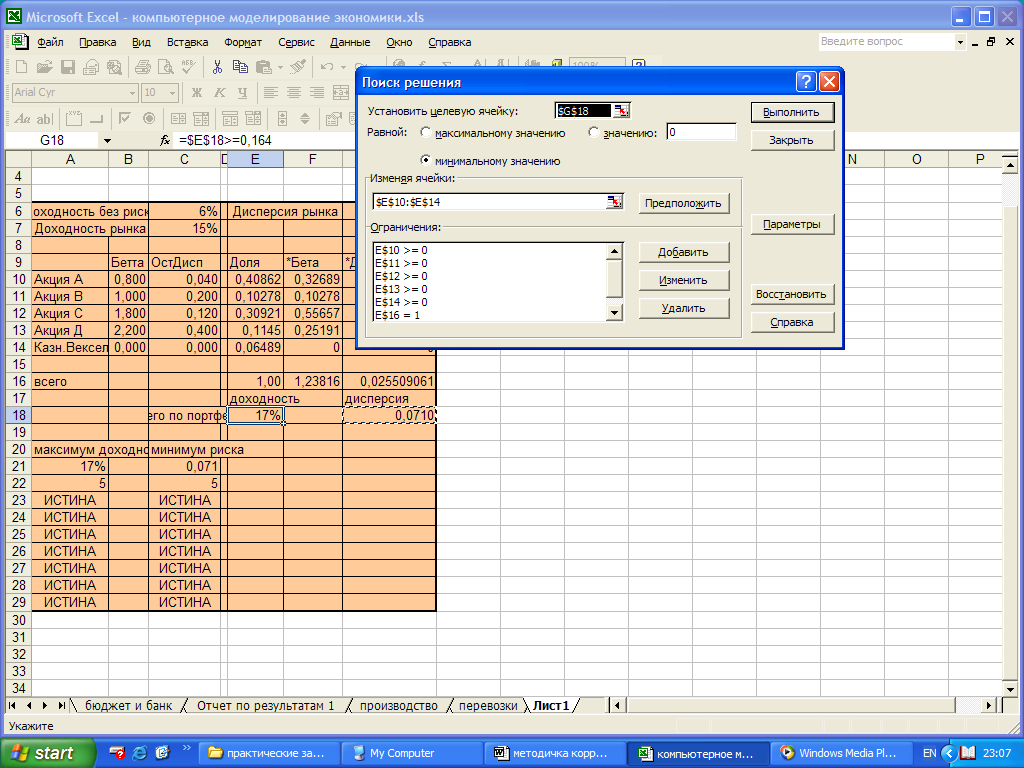
Рис. 1.64. Диалоговое окно программы Поиск решения после загрузки модели
Рис
1.65. Сформированный
портфель ценных бумаг
Контрольные вопросы:
Для решения каких задач используется процедура Поиска решения?
Какую ячейку называют «целевой»?
Для чего применяются ограничения в процессе поиска решений?
Относительная ссылка в формуле - это адрес ячейки, определяемый на основе расположения этой ячейки относительно ячейки, содержащей ссылку. При копировании ячейки относительная ссылка автоматически изменяется.
Абсолютная ссылка ячейки в формуле, например $A$1, всегда ссылается на ячейку, расположенную в определенном месте. При изменении позиции ячейки, содержащей формулу, абсолютная ссылка не изменяется. При копировании формулы вдоль строк и вдоль столбцов абсолютная ссылка не корректируется. По умолчанию в новых формулах используются относительные ссылки, и для использования абсолютных ссылок надо выбрать соответствующий параметр. В формуле абсолютная ссылка на ячейку имеет вид - $A$1.
1Линии тренда позволяют графически отображать тенденции данных и прогнозировать их дальнейшие изменения. Подобный анализ называется также регрессионным анализом. Регрессионный анализ - форма статистического анализа, используемого для прогнозов. Регрессионный анализ позволяет оценить степень связи между переменными, предлагая механизм вычисления предполагаемого значения переменной из нескольких уже известных значений. Используя регрессионный анализ, можно продлить линию тренда в диаграмме за пределы реальных данных для предсказания будущих значений.
Настройки программы Microsoft Excel позволяют дополнить линию тренда значением квадрата смешанной корреляции - R в квадрате. Коэффициент R в квадрате отражает близость значений линии тренда к фактическим данным и представляет собой значение в пределах от 0 до 1. Линия тренда в наибольшей степени приближается к представленной на диаграмме зависимости, если значение равно или близко к 1.При аппроксимации данных с помощью линии тренда значение R-квадрат рассчитывается автоматически. Полученный результат можно вывести на диаграмме.
Режим Подбор параметра реализует алгоритм численного решения уравнения, зависящего от одной или нескольких переменных.
Процесс решения с помощью данного метода распадается на два этапа:
1. Задание на рабочем листе ячеек, содержащих переменные решаемого уравнения (так называемых влияющих ячеек), и ячейки, содержащей формулу уравнения (зависимой или целевой ячейки).
2. Ввод адресов влияющих и целевой ячеек в диалоговое окно Подбор параметра и получение ответа (или сообщения о его отсутствии/Невозможности найти).
Подбор параметра является частью блока задач, который используется тогда, когда желаемый результат известен, но неизвестны значения, которые требуется ввести для получения этого результата. Подбор параметра - способ поиска определенного значения ячейки путем изменения значения в другой ячейке. При подборе параметра значение в ячейке изменяется до тех пор, пока формула, зависящая от этой ячейки, не вернет требуемый результат.
* Термин «возвращает» применительно к функциям рабочего листа электронных таблиц означает результат действия функции.
При наборе формулы используйте ввод адресов ячеек с помощью выбора нужных ячеек мышью, вводя вручную только символ = и две кавычки.
* Функция СУММЕСЛИ складывает цифры, если они отвечают определенным условиям. Структура функции такова:
СУММЕСЛИ(интервал;критерий;сумм_интервал).
Значения параметров функции следующие:
• Интервал — это массив ячеек, по которому проверяется условие суммирования;
• Критерий — это условие суммирования в форме числа, выражения или текста, — например, критерий может быть выражен как 32, «32», «>32», «яблоки»;
• Сумм_интервал — это массив ячеек, параллельный массиву Интервал, по которому осуществляется суммирование; ячейки в сумм_интервал суммируются, только если соответствующие им ячейки в аргументе интервал удовлетворяют критерию.