
- •Рекомендовано заседанием кафедры вм и и
- •Определители и их свойства
- •Обратная матрица. Ранг матрицы
- •Системы линейных уравнений
- •Векторы. Линейные операции над векторами
- •1.44. Линейный оператор в базисе задан матрицей а. Найти образгде:
- •Раздел 2. Элементы аналитической геометрии Прямая на плоскости
- •Прямая и плоскость в пространстве
- •Раздел 3. Введение в математический анализ
- •Предел последовательности и его свойства
- •Предел и непрерывность функции
- •Формулыдифференцирования
- •Правила дифференцирования
- •Эластичность функции
- •Общая схема исследования функции и построения графика
- •Дифференциал функции
- •Раздел 4. Интегральное исчисление функции одной переменной Неопределенныйинтеграл
- •Свойства неопределенного интеграла
- •Метод замены переменной
- •Определенный интеграл Основные свойства определенного интеграла
- •Правила вычисления определенного интеграла
- •Несобственные интегралы
- •Раздел 5. Функции нескольких переменных
- •Раздел 6. Дифференциальные уравнения
- •Раздел 7. Ряды
- •Библиографический список
Раздел 3. Введение в математический анализ
Дифференциальное исчисление функции одной переменной
Предел последовательности и его свойства
3.1.Доказать,
используя определение предела
последовательности, что
![]() :
:
1)
![]() 2)
2)
![]() ;
;
3)
![]() 4)
4)
![]() .
.
Найти


![]()
![]() 1)
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() 6)
6)
![]() ;
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ; 10)
; 10)
![]() ;
;
11)
![]() ; 12)
; 12)
![]() .
.
3.3.
Вычислить пределы, используя равенство
![]() :
:
1)![]() 2)
2) ![]() 3)
3)
![]() ;
;
4)![]() ;
5)
;
5)![]() 6)
6)![]() .
.
Предел и непрерывность функции
3.4. Доказать, используя определение предела функции, что
1)
![]() 2)
2) ![]()
3)
![]() ; 4)
; 4) ![]() .
.
3.5. Найти пределы:
1)
![]() 2)
2) ![]()
3)
![]() ; 4)
; 4) 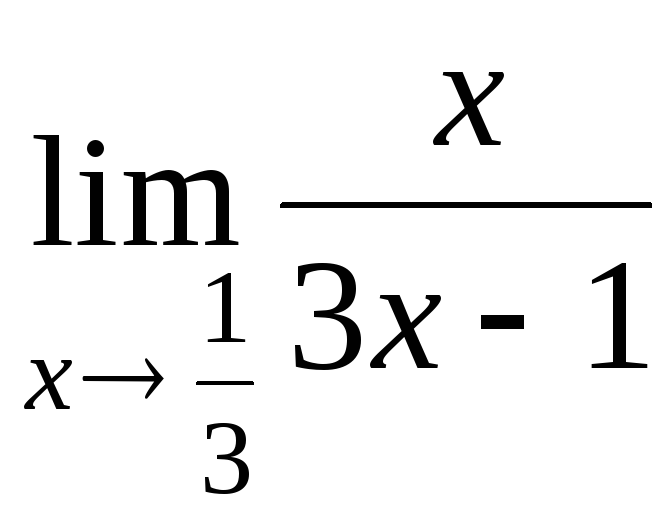 ;
;
5)
 ;
6)
;
6) ![]() ;
;
7)
![]() ;
8)
;
8) ![]() ;
;
9)
![]() ; 10)
; 10) ![]() ;
;
11)
![]() ;
12)
;
12) ![]() ;
;
13)![]() ;
14)
;
14)![]() ;
15)
;
15) ![]() ;
16)
;
16) ![]() ;
;
17)
![]() ; 18)
; 18) ![]() ;
;
19)
![]() ;
20)
;
20) ![]() ;
;
21)
![]() ;
22)
;
22)![]() .
.
3.6. Найти пределы :
1)
 ;
2)
;
2)  ;
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
![]() ;
;
11)
![]() ;
12)
;
12)
 ;
;
13)
![]() ;
14)
;
14)
![]() ;
;
15)
![]() ;
16)
;
16)
![]() ;
;
17)
![]() ;
18)
;
18)
![]() ;
;
19)
![]() ; 20)
; 20)
![]() ;
;
21)
![]() ;
22)
;
22)
![]()
23)
![]() ;
24)
;
24)
![]()
.
3.7. Исследовать функции на непрерывность:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
 ; 4)
; 4)
![]() ;
;
5)
 ;
6)
;
6)
![]() ;
;
7)
![]() ;
8)
;
8)
 ;
;
9)
 ; 10)
; 10)
 .
.
Формулыдифференцирования
1.
(![]() )'
=
)'
=
![]() ;
частный случай: (
;
частный случай: (![]() )'
=
)'
=![]() .
.
2.
(![]() )'
=
)'
=
![]()
![]() ;
частный случай:
;
частный случай:
![]()
3.
(![]() )'
=
)'
=
![]() ;
частный случай: (
;
частный случай: (![]() )'
=
)'
=
![]() .
.
4. (sinx)' = cosx . 5. (cosx)' = -sinx .
6.
(tgx)' =
![]() .
7. (ctgx)' =
.
7. (ctgx)' =
![]() .
.
8.
(arcsinx)' =
![]() .
9. (arccosx)' = –
.
9. (arccosx)' = –![]() .
.
10.
(arctgx)' =
![]() .
11. (arcctgx)' = –
.
11. (arcctgx)' = –![]() .
.
Правила дифференцирования
1.![]() 2. (
f
+ g
) ´
=
2. (
f
+ g
) ´
=
![]() 3.
3.
![]() .
.
4.
![]() 5.
5.
![]() =
=
![]() .
6.
.
6.
![]()
Здесь С – постоянная f = f(x), g = g(x) – дифференцируемые функции.
3.8. Найти производные функций по определению производной:
1)
y =
![]() ;
2) y =
;
2) y =
![]() ;
3) y =
;
3) y =
![]() ;
;
4)
y = sin x;
5) y = cos x
; 6) y =
![]() .
.
3.9. Найти производные функций:
 ;
;
 ;
;
3)
![]() ;
4)
;
4)![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
![]() ;
;
11)
![]() ;
12)
;
12)
![]() ;
;
13)
![]() ;
14)
;
14)
![]() ;
;
15)
![]() ;
16)
;
16)
![]() ;
;
17)
![]() ; 18)
; 18)![]() ;
;
19)
![]() ;
20)
;
20)![]() ;
;
21)
![]() ;
22)
;
22)![]() ;
;
23)
![]() ;
24)
;
24)![]() ;
;
25)
![]() ;
26)
;
26)
![]() ;
;
27)
 ;
28)
;
28)
![]() ;
;
29)
![]() ; 30)
; 30)
![]() ;
;
31)
![]() ; 32)
; 32)
![]() .
.
3.10. Найти y´:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)![]() ;
6)
;
6)
![]() ;
;
7)
![]() ;
8)
;
8)
![]() .
.
3.11. Найти производные функций и вычислить их значения
при x = x0:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]()
3.12. Найти производные функций, заданных неявно:
1)
![]() ;
2)
;
2) ![]() ;
;
3)![]() ;
4)
;
4) ![]() ;
;
5)
![]() ;
6)
;
6) ![]() .
.
3.13.
Обьем продукции u
(усл.ед.) в течение рабочего дня представляет
функцию u
=
![]() ,
где t
– время (ч). Найти производительность
труда, скорость и темп ее изменения
через 2 часа после начала работы; за 1
час до ее окончания (при 8 часовом рабочем
дне).
,
где t
– время (ч). Найти производительность
труда, скорость и темп ее изменения
через 2 часа после начала работы; за 1
час до ее окончания (при 8 часовом рабочем
дне).
3.14.
Зависимость между издержками производства
y
(ден.ед.) и объемом выпускаемой продукции
х (ед.) выражается функцией
y
=![]() . Определить средние и предельные
издержки при обьеме продукции, равном
5 ед.
. Определить средние и предельные
издержки при обьеме продукции, равном
5 ед.
