
- •1 Выбор электродвигателя и кинематический расчет привода
- •1.2 Определение расчетной мощности электродвигателя
- •1.3 Определение среднеквадратичной мощности электродвигателя
- •1.4 Выбор электродвигателя и разбивка общего передаточного числа привода по ступеням
- •1.5 Определение частоты вращения валов привода
- •2.13 Определение окружной силы
- •2.14 Определение числа ремней
- •2.15 Определение силы предварительного натяжения
- •2.16 Определение максимального напряжения в ремне
- •2.17 Определение срока службы ремня
- •3 Расчет закрытой косозубой цилиндрической передачи
- •3.1 Определение межосевого расстояния из условия контактной выносливости зубьев
- •3.2 Рабочая ширина зубчатых колес
- •3.13 Расчет зубьев на выносливость при изгибе
- •4 Предварительный расчет валов
- •5 Конструктивные размеры элементов передач
- •6 Проверка прочности шпоночных соединений
- •6.1Цилиндрическое колесо:
- •6.2 Ведущий шкив ременной передачи:
- •6.3 Ведомый шкив ременной передачи
- •7 Конструктивные размеры корпуса редуктора
- •7.1 Цилиндрический редуктор
- •8. Определение реакций в опорах подшипников.
- •9 Проверка долговечности подшипников
- •10. Уточненный расчет валов
- •11. Выбор сорта масла
- •12. Выбор посадок
- •13. Технология сборки редуктора
3.13 Расчет зубьев на выносливость при изгибе
Условие прочности:
σF=YF YE
YE YB
YB σFP
(3.47)
σFP
(3.47)
где σF- напряжение при изгибе, МПа;
YF- коэффициент, учитывающий форму зубьев. Выбирается в зависимости от эквивалентного числа зубьев шестерни и колесаZν1 иZν2 ;
YE- коэффициент, учитывающий перекрытие зубьев;
YB- коэффициент, учитывающий наклон зубьев;
ωFt- удельная расчетная окружная сила при расчете на изгиб, Н/мм;
m - модуль зацепления, мм;
σFP– допускаемое напряжение изгиба, МПа.
Zν1= =
= (3.48)
(3.48)
Zν2= =
= (3.49)
(3.49)
Принимаем при Zν1=28YF1=3.88 иZν2=112YF2=3,60 (таблица 2.9)
Для косозубой передачи YE=1
YB=1- (3.50)
(3.50)
ωFt= (3.51)
(3.51)
где FFt- исходная окружная расчетная сила при расчете на изгиб, Н;FFt=FHt=2861H.
KFα- коэффициент, учитывающий распределение нагрузки между зубьями, который определяется по таблице 2.10 или по формуле
KFα= (3.52)
(3.52)
где n – степень точности
KFα=
KFβ- коэффициент, учитывающий распределение нагрузки по ширине зубчатого венца.
При величине ψbdи НВ ≤ 350 при симметричном расположении зубчатых колес относительно опор принимаемKFβ=1,19 (рисунок 3)
KFν- коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении.
KFν=1+νF (3.53)
где νF- динамическая добавка при расчете на изгиб

где ωFν- удельная окружная динамическая сила при расчете на изгиб, Н/мм.
По аналогии с расчетом на контактную выносливость ωFν=ωHν=1,453H/мм
KFν=1+0,054=1,054
Тогда получаем
ωFt= Н/мм
Н/мм
Отсюда следует, что
σF1=2.798 0.941
0.941 МПа
МПа
σF2=σF1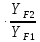 =65
=65 = 60 МПа (3.54)
= 60 МПа (3.54)
σFP= YR
YR YS
YS KXF
(3.55)
KXF
(3.55)
где σFeim- предел выносливости материала зубьев при изгибе, соответствующий эквивалентному числу циклов перемены напряжений, МПа.
YR- коэффициент, учитывающий шероховатость переходной поверхности зуба. Для класса шероховатости не ниже 4YR=1 ;
YS- коэффициент, учитывающий градиент напряжений и чувствительность материала к концентрации напряжений, зависит от модуля зацепления; приm=2ммYs=1,03 (таблица 2.11);
KXF – коэффициент, учитывающий размер зубчатого колеса. Выбирается в зависимости от диаметра вершин зубьев зубчатого колеса. Приda2=223KXF=1 (таблица 2.12).
σFeim=σ0Flim KFg
KFg KFd
KFd KFC
KFC KFl
(3.56)
KFl
(3.56)
где σ0Flim- предел выносливости материала зубьев при изгибе, соответствующий базовому числу циклов перемены напряжений, МПа.
KFg- коэффициент, учитывающий влияние шлифования переходной поверхности зуба. Для нешлифованных зубчатых колесKFg=1,1 (таблица 2.13).
KFd- коэффициент, учитывающий влияние деформационного упрочнения и электрохимической обработки переходной поверхности. ПринимаемKFd=1,1 (таблица 2.13).
KFC- коэффициент, учитывающий влияние двухстороннего приложения нагрузки (реверсивность нагрузки)
KFC=1-ɣFC (3.57)
(3.57)
где ɣFC- коэффициент, учитывающий влияние амплитуд напряжений противоположного знака. Для зубчатых колес из термоулучшенной или нормализованной стали ɣFC=0,35 ;
T1F- исходная расчетная нагрузка, действующая в прямом направлении вращения, Нм;
TF- исходная расчетная нагрузка, действующая при реверсе передачи, Нм. Так как график нагрузки соответствует как прямому направлению вращения, так и реверсивному, тоTF=T1F
n1циnц - числа циклов перемены напряжений соответственно при прямом направлении вращения и при реверсе. Для вышесказанногоn1ц=nц. Тогда:
 =1
=1
KFC=1-0.35 1=0.65
1=0.65
KFl– коэффициент долговечности
KFl= (3.58)
(3.58)
где NFO- базовое число циклов перемены напряжений
изгиба.NFO=4 106
106
NFE- эквивалентное число циклов перемены напряжений. Определяется в зависимости от данных графика нагрузки.
При НВ ≤ 350 mF=6 . При НВ > 350mF=9
При постоянном значении частоты вращения зубчатых колес ni=n=const
Для шестерни:
NFE1=60 tч
tч n1
n1 [(
[( )6
)6 + (
+ ( )6
)6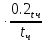 + (
+ (
 )6
)6 ]
(3.59)
]
(3.59)
Для колеса
NFE2=60 tч
tч [(
[( )6
)6 + (
+ ( )6
)6 + (
+ (
 )6
)6 ]
(3.60)
]
(3.60)
где T1FiиT2Fi- частные значения нагрузок на шестерне и колесе, соответствующие i-тым участкам графика нагрузки, Нм;
T1FиT2F- наибольшее значение длительно действующих нагрузок на шестерне и колесе, Нм;
tчi- частные значения длительностей нагрузок на i-тых участках графика нагрузки, час;
tч- срок службы передачи, час.
NFE1=60 13.5
13.5 2913
2913 (1
(1 0.4+0.86
0.4+0.86 0.2+0.46
0.2+0.46 0.4)
= 2359
0.4)
= 2359 106
106
 (3.61)
(3.61)
При NFE > NFO KFl=1. Принимаем KFl1=KFl2=1 (п.2.2)
Для нормализованной и улучшенной стали:
σ0Flim1=1,8HB1=1,8 280=504МПа
(3.62)
280=504МПа
(3.62)
σ0Flim2=1,8HB2=1,8 260=468МПа
(3.63)
260=468МПа
(3.63)
Тогда имеем
σFeim1=504 1.1
1.1 1.1
1.1 0.65
0.65 1=396.4МПа
1=396.4МПа
σFeim2=468 1.1
1.1 1.1
1.1 0.65
0.65 =368.1МПа
=368.1МПа
SF - коэффициент безопасности.
SF=SF′ SF′′
(3.64)
SF′′
(3.64)
где SF- коэффициент, учитывающий нестабильность свойств материала зубчатого колеса и ответственность передачи, принимаемS′F=1,75 (таблица 2.13);
S′′F- коэффициент, учитывающий способ получения заготовки зубчатого колеса:
S′′F=1 (для штамповок и поковок)
S′′F=1,15 (для проката)
S′′F=1,3 (для литых зубчатых колес)
Принимаем S′′F=1.
Тогда
SF=1,75 1=1,75
1=1,75
В этом случае имеем
σFP1
= ( )
) 1
1 1.065
1.065 1
= 226,5МПа
1
= 226,5МПа
σFP2
= ( )
) 1
1 1.065
1.065 1
= 210,34МПа
1
= 210,34МПа
Условие прочности выполнено:
σF1=65 МПа ≤σFP1=226,5 МПа
σF2=60 МПа ≤σFP2=210,34 МПа
