Множественная регрессия(реферат)

Министерство Образования Российской Федерации

Российский Государственный Гуманитарный Университет

Факультет информатики

Реферат по дисциплине:

«Прикладная статистика»

на тему: «Множественная регрессия в пакетах SPSS»

Выполнила: студентка 3 курса, ФИ, 1 группы

Проверил: Синицын В.Ю.

Москва 2005

Введение

SPSS - одна из старейших систем статистического анализа и управления данными, продукт фирмы SPSS Inc. (Statistical Products and Service Solution - Статистические продукты и сервисные решения), сегодня SPSS является одним из лидеров среди универсальных статистических пакетов.

Системные требования. Для работы базовой системы требуется процессор 386 (рекомендуется процессор 486/33Мгц), 4 Мб памяти (рекомендуется 8 Мб), Windows 3.1 или старше, 20 Мб пространства на диске.

Интерфейс. Пакет SPSS построен как традиционная база данных: накопление массива информации, его формализация и представление результатов статистической обработки массива в виде отчета. Но так как пакет предназначен для выполнения специализированной функции - обработки результатов опросов - он имеет структурное отличие от традиционных баз данных, выраженное в принципах формализации накопляемого массива исходной информации, принципах статистической обработки и представления результатов информации.

Но внешних отличий интерфейса от традиционных баз данных или электронных таблиц (MS Access, MS Excel и т.п.) нет, что значительно упрощает первое знакомство с пакетом и позволяет достаточно быстро начать процедуру ввода или импорта данных, кроме того, пакет включает справочник и глоссарий статистических терминов.

Множественный регрессионный анализ

Экономические явления, как правило, определяются боль­шим числом одновременно и совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимо­сти одной зависимой переменной Y от нескольких объясняющих переменных Эта задача решается с помощью множественного регрессионного анализа.

Обозначимнаблюдение переменной, а объясняющих переменных —Тогда модель множественной линейной регрессии можно представить в виде:

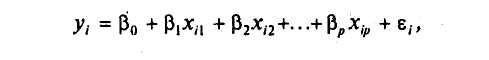
гдеаудовлетворяет приведенным выше предпосылкам.

Включение в регрессионную модель новых объясняющих пере­менных усложняет получаемые формулы и вычисления. Это приво­дит к целесообразности использования матричных обозначений. Матричное описание регрессии облегчает как теоретические кон­цепции анализа, так и необходимые расчетные процедуры.

Введем обозначения:— матрица-столбец, или вектор, значений зависимой переменной размера:

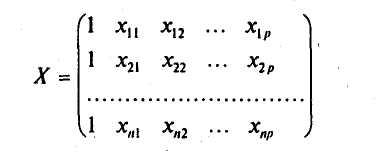
— матрица значений объясняющих переменных, или матрица плана размераобращаем внимание на то, что в матрицу X дополнительно введен столбец, все элементы которого равны 1, т.е. условно полагается, что в модели свободный член умножается на фиктивную переменную х_i0, принимающую зна­чение 1 для всех

— матрица-столбец, или вектор, параметров размера— матрица-столбец, или вектор случайных ошибок {возмущений) размера п.

Тогда в матричной форме модель примет вид:

Оценкой этой модели по выборке является уравнение где:

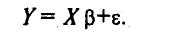
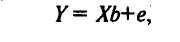
Для оценки вектора неизвестных параметровприменим ме­тод наименьших квадратов. Так как произведение транспониро­ванной матрицына саму матрицу

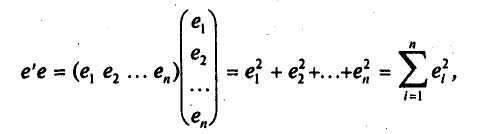
то условие минимизации остаточной суммы квадратов запишет­ся в виде:

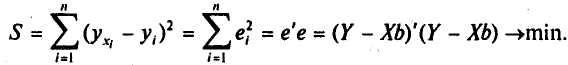
Учитывая, что при транспонировании произведения матриц по­лучается произведение транспонированных матриц, взятых в обрат­ном порядке, т.е., получим после раскрытия скобок:

Произведение есть матрица размера

, т.е. величина скалярная, следовательно, оно не меняется при транспонировании:. Поэтому условие минимизации примет вид:

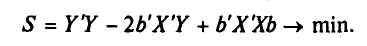
На основании необходимого условия экстремума функции не­скольких переменных, представляющей, не­обходимо приравнять нулю частные производные по этим пере­менным или в матричной форме — вектор частных производных

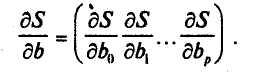
Для вектора частных производных доказаны следующие формулы:

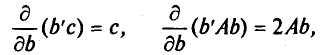
гдеи— вектор-столбцы, а— симметрическая матрица, в которой элементы, расположенные симметрично относительно главной диагонали, равны. Поэтому, полагая, а матрицу

(она является симметрической), найдем

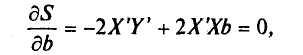
откуда получаем систему нормальных уравнений в матричной форме для определения вектора:

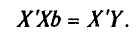
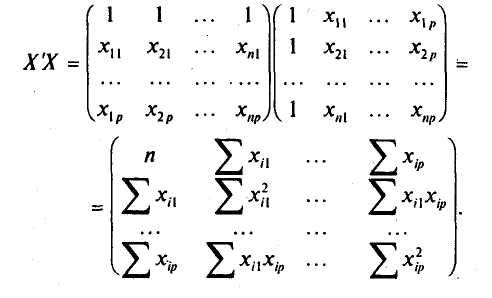
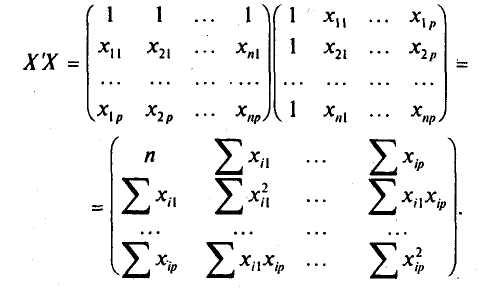
Найдем матрицы, входящие в это уравнение. Матрица Х'Х представляет матрицу сумм первых степеней, квадратов и по­парных произведений п наблюдений объясняющих переменных

Матрица есть вектор произведений п наблюдений объ­ясняющих и зависимой переменных:

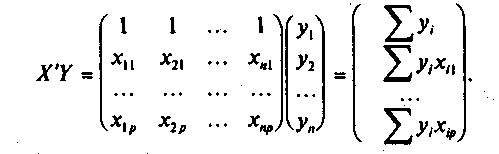
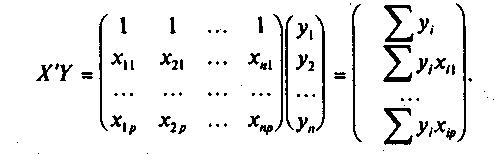В частном случае из рассматриваемого матричного уравнения с учетом и для одной объясняющей переменнойнетрудно получить уже рассматриваемую систему нормальных уравнений для несгруппированных данных. Действительно, в этом случае матричное уравнение при­нимает вид:

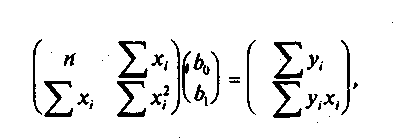
откуда непосредственно следует система нормальных уравнений для несгруппированных данных.

Для решения матричного уравнения относительно вектора оценок параметровнеобходимо ввести еще одну пред­посылку б для множественного регрессионного анализа: матрица является неособенной, т.е. ее определитель не равен нулю. Следовательно, ранг матрицы равен ее порядку, т.е.

. Из матричной алгебры известно, что, значит, т.е. столбцы матрицы планадолжны быть линейно независимыми.

Решением уравнения является вектор

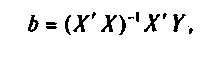
где— матрица, обратная матрице коэффициентов системы), а— матрица-столбец, или вектор, ее свобод­ных членов.

Зная вектор, выборочное уравнение множественной рег­рессии представим в виде

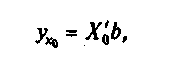
где— групповая (условная) средняя переменнойпри за­данном векторе значений объясняющей переменной

На практике часто бывает необходимо сравнение влияния на зависимую переменную различных объясняющих переменных, когда последние выражаются разными единицами измерения. В этом случае используют стандартизованные коэффициенты рег­рессиии коэффициенты эластичности:

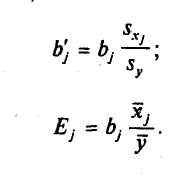
Стандартизованный коэффициент регрессии показывает, на сколько величинизменится в среднем зависимая переменнаяпри увеличении толькообъясняющей переменной на, а коэффици­ент эластичности— на сколько процентов (от средней) изменит­ся в среднемпри увеличении только на 1%.

Пример использования Линейной регрессии в SPSS

Линейный регрессионный анализ позволяет получить предсказание значений зависимой переменной на основе значений независимых переменных.

Линейный регрессионный анализ является достаточно сложной статистической процедурой. Поэтому здесь ограничимся рассмотрением случая одной зависимой и одной независимой переменной и будем использовать процедуру простой линейной регрессии.

Для расчета линейной модели регрессии необходимо использовать пункты меню

Statistics – Regression - Linear –

выбрать переменную и поместить ее в окно Dependent (зависимая переменная) – выбрать переменную и поместить ее в окно Independet(s) (независимые переменные).

Нажав кнопку Statistics… можно задать расчет ряда коэффициентов регрессии, нажав кнопку Plots… - вид выводимых графиков в процедуре линейной регрессии (см. рис. 2.20), можно задать сохранение результатов процедуры "Линейная регрессия" (кнопка Save…) и параметры процедуры регрессии (кнопка Options…)

При интерпретации результатов, полученных в окне вывода программы SPSS, необходимо учитывать, что некоторые выходные данные требуются только при построении сложных регрессионных моделей. Поэтому рассмотрим только основные элементы выходных данных. В сноске к таблице Model Summary дается информация, которая показывает, насколько хорошо можно представить значение зависимой переменной на основе независимой:

R – коэффициент корреляции между переменными;

R-square - квадрат коэффициента корреляции (показывает, какая часть изменчивости зависимой переменной может быть объяснена независимой переменной).

При интерпретации выходных данных необходимо учитывать значимость коэффициентов (столбец Sig. таблицы ANOVA): линейная регрессионная модель зависимости является надежной, если уровень значимости не превышает 0.05 (5%).

В таблице Coefficients (коэффициенты) приводятся рассчитанные коэффициенты регрессионной модели: регрессионный коэффициент (тангенс угла наклона прямой), а также постоянная прямой. Значение в первой строке столбца В таблицы (Constant) – постоянная, во второй (где приведено имя переменной) – коэффициент (тангенс угла наклона прямой). С помощью этих чисел можно записать уравнение прямой:

Зависимая переменная = Коэффициент * Независимая

переменная + Постоянная

Теперь, используя это уравнение, можно по заданному значению независимой переменной вычислять значения (предсказанные) зависимой переменной.

В столбце Sig. таблицы Coefficients представлен уровень значимости для каждого регрессионного коэффициента. При 5%-ном уровне значимости можно считать неравными нулю только те коэффициенты, для которых значение Sig. не превышает 0.05.

Литература:

1. Сайт:

http://spss.ru

http://www.5ballov.ru/

2. Н.Ш. Кремер

«Теория вероятности и математическая статистика»

3. Руководство по использованию программы статистической обработки SPSS.

4. С.Ф. Борисова

«Компьютер и Интернет для социолога»