Кванты / Квантовая мех.pdf / sem6
.docСеминар 6. Общие принципы вычислений
6.1 Основные понятия алгебры логики
Алгебра логики — раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логических (истина или ложь) значений, и логические операции над ними.
Алгебралогикивозниклавсередине19векавработахДж.БуляибыларазвитаЧ.Пирсом
(C.S. Peirs),П.С.Порецким,Б.Расселом(B.Russel),Д.Гильбертом(D.Hilbert)идр.
Высказываниемназываютсяпредложения,которыемогутбытьохарактеризованыпонятием—истинаилиложь.Использованиелогическихсвязок"и","или","если...то","эквивалентно",частица"не"ит.д.позволяетстроитьновые,болеесложные,высказыванияиззаданных.Истинностьилиложностьсложныхвысказыванийзависитотистинностиилиложностиисходныхвысказываний.Дляобозначенияистинностивводятсятождественныесимволы:
Истина ≡ И ≡ True ≡ T ≡ 1. (6.1)
Для обозначения ложности высказывания вводятся следующие тождественные символы
Ложь ≡ Л ≡ False ≡ F ≡ 0. (6.2)
Соответственно для логических связок приняты следующие обозначения:
"и"(конъюнкция) ≡ & ≡∧≡ AND ≡∩"или"(дизъюнкция) ≡∨≡ OR"если...то"(импликация)≡→"эквивалентность" ≡∼
"отрицание" ≡ черта над высказыванием ≡¬≡ NOT
⎫
⎬
(6.3)
Связкиичастицы"не"рассматриваютсявалгебрелогикикакоперациинадвеличинами,принимающиедвазначения0и1,авысказыванияспроизвольнымивысказываниямиисвязкамиобразуютформулы.Приэтомвысказывания,образующиеформулу,рассматриваютсявкачествепеременных,асвязкивкачествефункций.ФормулыAиBназываютсяравными(A=B),еслиониреализуютравныефункции.
Для задания функций алгебры логики, используются таблицы, содержащие все наборы значений переменных и значений функций: такие таблицы называются таблицами истинности. Пример таблицы истинности для NOT, AND, OR, импликации и эквивалентности приведены ниже
|
a |
b |
NOT a |
a ∧ b |
a ∨ b |
a → b |
a ∼ b |
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
Сложные формулы в алгебре логики могут быть преобразованы. Для преобразования формул основную роль играют следующие законы:
– закон коммутативности
a ∨ b = b ∨ a; a ∧ b = b ∧ a; (6.4)
– закон ассоциативности
(a ∧ b) ∧ c = a ∧ (b ∧ c);(a∨ b) ∨ c = a ∨ (b ∨ c);(6.5)
– закон поглощения
a ∧ (a ∨ b)=a;a∨ (a ∧ b)=a;(6.6)
– закон дистрибутивности
a ∧ (b ∨ c)=(a∧ b) ∨ (a ∧ z);a∨ (b ∧ c)=(a∨ b) ∧ (a ∨ c);(6.7)
– закон противоречия
a ∧ a = 0; (6.8)
– закон исключения третьего
a ∨ a = 1; (6.9)
a → b = a ∨ b; a ∼ b =(a ∧ b) ∨ (a ∧ b) (6.10)
Множество всех формул, в построении которых учавствуют переменные высказывания, символы ∧, ∨, →, ∼, ¬, константы 0 и 1 называются языком над данными символами. Равенство (6.4)–(6.10) означают, что для всякой формулы в языке над ∧, ∨, →, ∼, ¬, 0, 1 найдется равная ей формула в языке над ∧, ∨,,0,1.
¬
Алгебралогикиразвиваласьподвлияниемприкладныхзадач,средикоторыхприложениектеорииэлектрическихсхемиграетсамоеважноезначение.Валгебрелогикиставитсязадачаминимизациифункцииприводязаданнуюфункциюкфункцииимеющейнаименьшеечислосомножителей,тоестьминимальнуюсложность.Такиефункцииназываютсяминимальными.
Вязыкенад ∧, ∨, →, ∼, 0, 1, ⊕,где ⊕ – используетсядляобозначениясложенияпомодулю 2 устанавливаются следующие соотношения:
a ∨ b = ((a ∧ b)+a)+b(6.11)a→ b = a ∧ b; a ∼ b=(a+b)+1;(6.12)a+b=(a∧ b) ∨ (a ∧ b);1=a∨ a. (6.13)
6.2 Классические универсальные машины и логические гейты
Универсальный компьютер — это логическое устройство, реализованное в виде сложной сети взаимосвязанных примитивных (основных) элементов. Для классического компьютера можно представить, что взаимосвязь элементов осуществляется идеальными проводниками, передающими одно из двух стандартных напряжений, представляющих локально один бит информации — 1 или 0. Сами примитивные элементы — или гейты реализуют функции преобразования, использующиеся в алгебре логики.
Классическийкомпьютеросуществляетвычислениефункцийпозаданнымвходнымn-битам,располагаярезультатвычислениявm-битах.Функциясm-битамизначенийэквивалентнаm-функциям,каждаяизкоторыхимеетоднобитовоезначениевкачестверезультата.Вычислениекаждойизэтихфункцийможетбытьсведенокпоследовательностиэлементарныхлогическийопераций(гейтов).
Символически гейты и биты, "соединенные проводами", изображаются рисунками.
Так на рисунке представлен примитивный элемент сети, в которой над битом выполняется логическая операция отрицания (NOT)
Нарисункеуказано,чтобитaпроходитчерезгейтNOT,которыйпереворачиваетбит,превращая1в0и0в1.ЛиниидоипослегейтаNOTслужатдляпереносабитакгейтуиудалениеегопослепреобразования.Данныелинии(провода)могутпредставлятькакпереносбитаизоднойточкипространствавдругую,такиразвитиесостояниябитавовремени.ГейтNOTимеетодинвходнойбитиодинбитнавыходе.Фактически,выходнойбитвычисляетфункциюf(a)=1⊕ a.
При построении сети предполагается, что сеть не содержит замкнутых петель.
Имеетсямногоиныхэлементарныхлогическихгейтов,полезныхдляорганизациипроцессавычисления,которыеимеютдвабитавкачествеисходныхданныхиодинрезультирующийбит.Геометрическиеизображения,алгебраическиеформулывбинарнойарифметикеитаблицыистинности,которыхприведеныниже
|
a |
b |
c |
|||
|
0 |
0 |
0 |
|||
|
; |
c ≡ a ∧ b = a · b |
0 1 |
1 0 |
0 0 |
|
|
|
|
1 |
1 |
1 |
|
б. OR-гейт
|
a |
b |
c |
||
|
0 |
0 |
0 |
||
|
; |
c ≡ a ∨ b = a + b − a · b |
0 1 |
1 0 |
1 1 |
|
|
|
1 |
1 |
1 |
в.
XOR-гейт
(исключающее или ≡
"или",
но не оба)
ab
00
; c ≡ aXORb=a(1− b)+b(1− a) 01
10 11
г.
NAND-гейт
≡
(NOT
AND-гейт)
ab
00 ; c =1 − ab 01
·
10
11 д. NOR-гейт
≡
(NOT
OR-гейт)
ab
00
; c = (1 − a)(1− b) 01 10 11
0 1 1 0
c
1 1 1 0
c
1 0 0 0
Любоевычислениеможетбытьзаписановтерминахбулевскоговыражения,илюбоебулевскоевыражениеможетбытьпостроеноизфиксированногонаборалогическихгейтов.Такойнабор(например,AND,ORилиNOT)называетсяуниверсальным.Вдействительностиможнообойтисьтолькодвумягейтами,такимикакANDиNOT,илиORиNOT,илиANDиXOR.Устройство,котороеможетисполнитьпроизвольныекомбинациилогическихгейтовизуниверсальногонабора,являетсяуниверсальнымкомпьютером.
Хотяприведенныевышегейтыдостаточныдляматематическогоаппаратаалгебрылогики,онинедостаточныдляреализациипрактическойвычислительноймашины.ВреальномустройстветребуютсяещедвагейтаFANOUT(разворачивание)иERASE(стирание).
FANOUT-гейтдублируетвходнойбит,агейтERASE–уничтожаетвходнойбит.ПосутиFANOUT-гейттребуетсядляорганизациивычислений,аERASEдляочисткиячеекпамятикомпьютера.
В некоторых приложениях используется, помимо того, гейт EXCHANGE
|
|
a 0 0 1 1 |
b |
|
0 1 0 1 |
||
|
50 |
|
|
|
a� |
b� |
|
0 |
0 |
|
1 |
0 |
|
0 |
1 |
|
1 |
1 |
Для примера рассмотрим цепь, которая суммирует два целых числа, имеющих длину nбит. Базовым элементом в этой цепи является "ячейка" сети известная как полусумматор (half-adder ≡ HA). На вход полусумматора подаются два бита x и y, а на выходе получается сумма битов x ⊕ y по модулю 2 и перенос (carry) бита в состоянии 1, если x и y оба 1, или 0 во всех остальных случаях.
Схема сети полусумматора имеет вид:
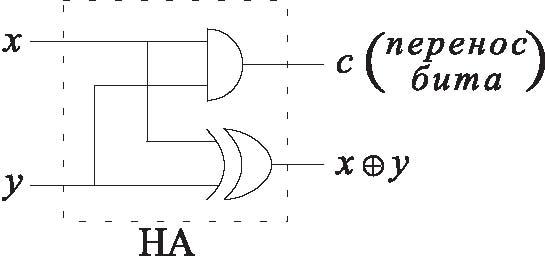
Таблица истинности полусумматора:
|
x |
y |
|
0 |
0 |
|
0 |
1 |
|
1 |
0 |
|
1 |
1 |
перенос 0 0 0 1
x ⊕ y
0 1 1 0
двоичное число
00 01 01 10
Перенос бита позволяет перейти на следующий разряд, если складывается 1+1=0. Каскад из 2-х полусумматоров (HA) образует полный сумматор (full-adder ≡ FA)
Полныйсумматоримееттрибитанавходе,гдеx,y–данныедлясложения,c–переносбитаспредыдущегоэтапавычисленийидвабитанавыходе.Одинвыходнойбитявляетсясуммойпомодулю2x⊕ y ⊕ cвсехтрехвходящихбитов,авторойвыходнойбитc�–естьпереносбита,которыйравен1,еслидваилибольшевходныхбитаравны1,иравен0впротивномслучае.
Таблица истинности полного сумматора: Каскадполныхсумматоров,позволяющийпостроитьцепьдлясложениядвух2-хбитовыхцелых(x1x0)+(y1y0)
|
x |
y |
c |
x |
y |
c |
x |
y |
c |
перенос |
x ⊕ y ⊕ c |
число |
|
0 0 1 1 |
0 1 0 1 |
0 0 0 0 |
0 0 0 1 |
0 1 1 0 |
0 0 0 0 |
0 0 0 1 |
0 0 0 0 |
0 1 1 0 |
0 0 0 1 |
0 1 1 0 |
00 01 01 10 |
|
0 0 1 1 |
0 1 0 1 |
1 1 1 1 |
0 0 0 1 |
0 1 1 0 |
1 1 1 1 |
0 0 0 1 |
0 1 1 0 |
1 0 0 1 |
0 1 1 1 |
1 0 0 1 |
01 10 10 11 |
|
x1 |
x0 |
y1 |
y0 |
x1 |
x0 |
y1 |
y0 |
c |
x0 |
y0 |
x + y |
10-тичное число |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
000 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
001 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
010 |
2 |
|
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
011 |
3 |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
001 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
010 |
2 |
|
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
011 |
3 |
|
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
100 |
4 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
010 |
2 |
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
011 |
3 |
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
100 |
4 |
|
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
101 |
5 |
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
011 |
3 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
100 |
4 |
|
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
101 |
5 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
110 |
6 |
Каскадполныхсумматоровпозволяетпостроитьцепьдлясложениядвухn-битовыхцелых.Примердляn=3приведеннарисункениже.
Здесьдватрехбитовыхцелыхчислапредставленыввидеx=x2x1x0иy=y2y1y0.Аналогичноможетбытьпостроенацепьвычисленияпроизвольнойфункции.
В классическом компьютере NOT и NAND-гейты осуществляются транзисторами, например, как показано на рис. 6.1.
рис. 6.1.
Минимальнаясвободнаяэнергия,котораярасходуетсянаточтобыработалидеальныйкомпьютерзависитотнабораичислапримитивныхэлементов.Например,нагейтеNAND,выходящаялинияc�принимаетодноиздвухзначенийиприэтомэнтропияизменяетсянаln2единицы.Теоретическийминимумколичестватеплоты,котороерассеиваетсявпространствонаодномэлементарномшагесоставляетkTln2(здесьk–постояннаяБольцмана,T–абсолютнаятемпература).Фактическивреальныхвычислительныхустройствахпроисходитдиссипацияэнергиипорядка∼ 1010 kT . Физически это связано с тем, что для изменения потенциала (напряжения) проводника он сначала заземляется через сопротивление, а затем через сопротивление заряжается.
Однако было установлено1, что предел kT ln2 не является абсолютным, так как нет необходимости использовать в вычислительном устройстве необратимые гейты. Оказалось, что все операции, требующиеся для проведения вычислений могут быть проведены обратимым образом, а следовательно без диссипации энергии (в соответствии с законами термодинамики).
Классические компьютеры построены на электрических цепях, содержащих миллионы транзисторов. На рисунке
6.2.
приведены результаты2
оценки
изменения числа примесей в основаниях
биполярных транзисторов, требующихся
для формирования логических операций
в зависимости от времени развития
полупроводниковых технологий.
По сути график отражает число электронов, необходимых для хранения одного бита информации. В соответствии с этими данными ясно, что технология достигает субатомные расстояния и фактически переходит на построение компьютеров на атомном и молекулярном уровне, что приводит к необходимости учета и включения
квантово-механических свойств вещества. Как будет показано ниже, на квантовых компьютерах программы выполняются посредством организации унитарной эволюции входных данных на квантовых объектах. А так как унитарные преобразования обратимы, то цепь логических гейтов должна основываться на обратимых операциях.