
ДМ_A7m / ДМ_А7m_4
.docИ.Е. Феоктистов
Дидактические и методические материалы
по алгебре для 7 класса с углубленным изучением математики
к учебнику «Алгебра. Учебник для 7 класса»
Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, И.Е. Феоктистова
М., «Мнемозина», 2007.
Тесты
Задания в тестовой форме в последние два десятилетия стали широко использоваться для проведения контроля знаний, умений и навыков учащихся при изучении математики. Составление таких заданий, их апробация являются делом не простым. По мнению специалистов, от момента создания теста до признания его приемлемым для использования в школе проходит от 3-х до 5 лет, и занимается этим не один человек, а целые коллективы. Поэтому тестовые задания для первичного закрепления материала – именно для этой цели наиболее пригодны, по моему мнению, задания в тестовой форме, – лучше не составлять самому, а использовать для этого тесты лаборатории аттестационных технологий МИПКРО1. За основу предложенных ниже тестов взят «Сборник тестовых заданий для тематического и итогового контроля по алгебре для 7 класса», «Интеллект-Центр», Москва, 1999, подобранных в соответствии с содержанием учебника «Алгебра. Учебник для 7 класса» Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, И.Е. Феоктистова, М., «Мнемозина», 2007.
Каждый тест содержит 6 заданий, рассчитанных на 15-20 минут. Тесты носят контролирующий характер, задания охватывают лишь основной материал учебника. Для того чтобы исключить возможность угадывания (а заодно и списывания, которое при выполнении заданий в тестовой форме выполняется значительно легче), учащимся нужно дать контрольное задание, подтверждающее самостоятельность выполнения заданий теста. Номер этого задания учитель должен назвать ученику непосредственно перед сдачей работы на проверку. Естественно, у разных учащихся должны быть разные контрольные номера. Учащихся нужно предупредить, что если они не решили контрольный номер, то за тест ставится оценка «2» (при этом считается, что ученик угадал или списал ответы всех заданий, а не только ответ одного контрольного номера). В случае если ученик получил неверный ответ (он, естественно, об этом не знает), он должен привести решение, приводящее к этому ответу. Естественно, этот номер не засчитывается как правильно выполненный, но зато считается, что ученик самостоятельно выполнял задания теста. Критерий оценки может быть таким: за три и четыре задания – «3», за пять заданий – «4», за шесть заданий – «5».
Тест 1
Числовые выражения (п. 3)
Вариант 1
-
Разность чисел
 и
и
 равна: 1)
равна: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Значение числового выражения
 равно: 1)
равно: 1)
 ;
2) 7; 3) 4; 4)
;
2) 7; 3) 4; 4)
 .
. -
Сумма числа
 и произведения чисел 2,5 и 16 равна: 1) 7,5;
2) 22; 3) 43,5; 4) 28.
и произведения чисел 2,5 и 16 равна: 1) 7,5;
2) 22; 3) 43,5; 4) 28. -
Число, противоположное частному чисел
 и 0,6, равно: 1) 0,4; 2)
и 0,6, равно: 1) 0,4; 2)
 ;
3)
;
3)
 ;
4) 4.
;
4) 4. -
Сумма 5% от числа 20 и 120% от числа 10 равна: 1) 13; 2) 22; 3) 15; 4) 11,2.
-
Туристы прошли 12 км пешком, а затем 3 часа ехали на машине со скоростью 60 км/ч. Весь путь туристов составляет: 1) 96 км; 2) 64 км; 3) 75 км; 4) 192 км.
Вариант 2
-
Разность чисел
 и
и
 равна: 1)
равна: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Значение числового выражения
 равно: 1) 7; 2)
равно: 1) 7; 2)
 ;
3)
;
3)
 ;
4) 3.
;
4) 3. -
Разность произведения чисел
 и
и
 и числа 2,4 равна: 1) 8,4; 2) 3,6; 3) 4,6; 4)
и числа 2,4 равна: 1) 8,4; 2) 3,6; 3) 4,6; 4)
 .
. -
Число, противоположное частному чисел 3,6 и
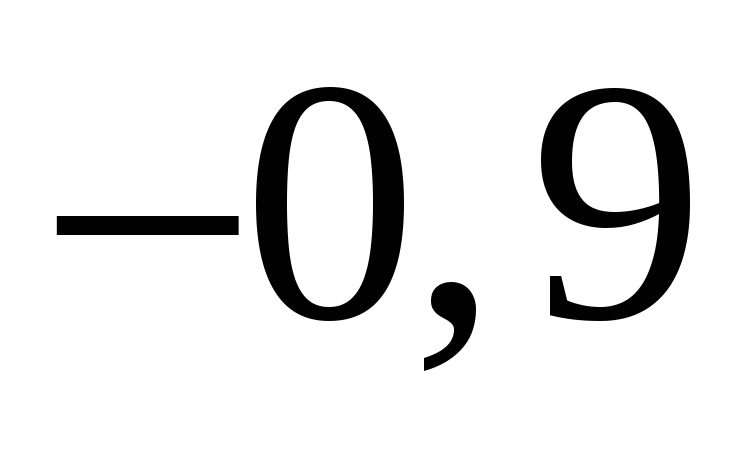 ,
равно: 1)
,
равно: 1)
 ;
2)
;
2)
 ;
3) 0,4; 4) 4.
;
3) 0,4; 4) 4. -
Сумма 3% от числа 50 и 110% от числа 4 равна: 1) 4,4; 2) 1,5; 3) 5,9; 4) 1,94.
-
На стройке работало 5 бригад по 10 человек в каждой и 3 бригады по 6 человек в каждой. Всего на стройке работало: 1) 128 строителей; 2) 68 строителей; 3) 40 строителей; 4) 58 строителей.
Тест 2
Выражения с переменными (п. 5)
Вариант 1
-
Значение выражения
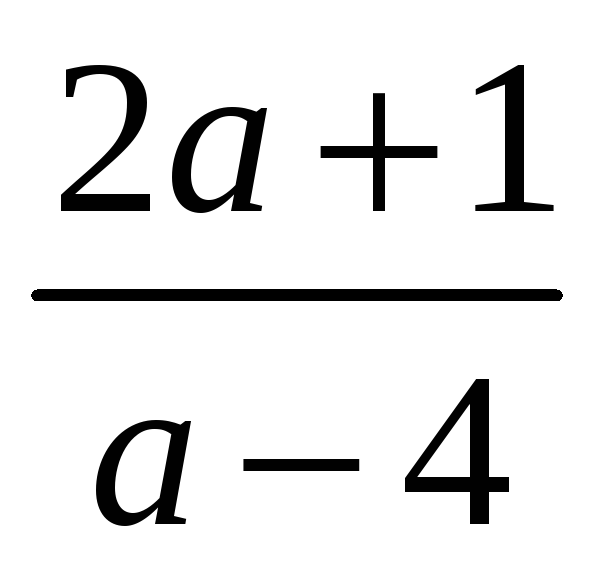 при
при
 равно: 1)
равно: 1)
 ;
2)
;
2)
 ;
3) 4; 4) 16.
;
3) 4; 4) 16. -
Выражение
 после приведения подобных слагаемых
будет равно: 1)
после приведения подобных слагаемых
будет равно: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Разность выражений
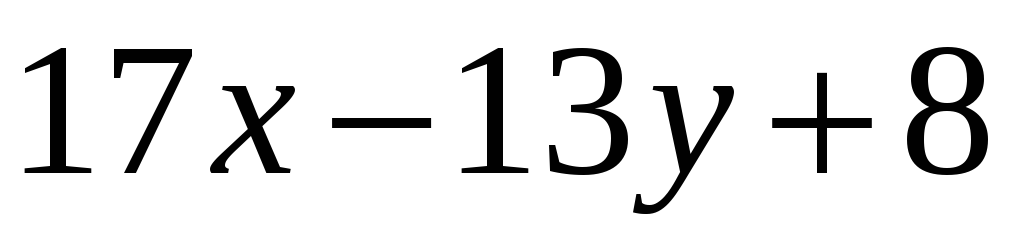 и
и
 равна: 1)
равна: 1)
 ;
2)
;
2)
 ;
3)
;
3)
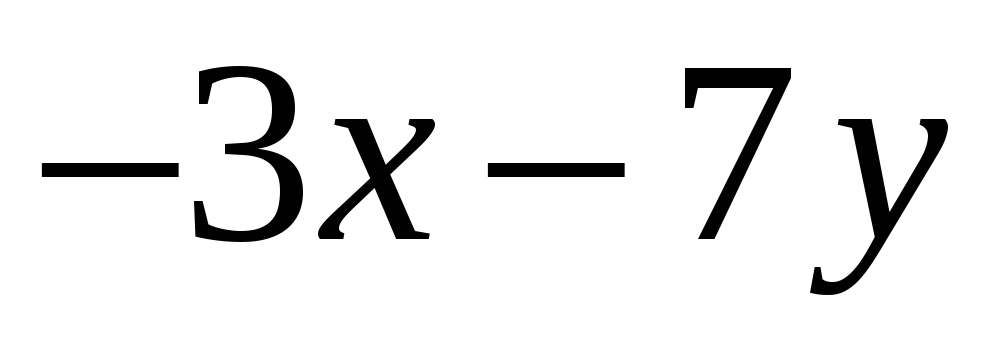 ;
4)
;
4)
 .
. -
Выражение
 после упрощения будет равно: 1)
после упрощения будет равно: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Выражение
 не имеет смысла при: 1)
не имеет смысла при: 1)
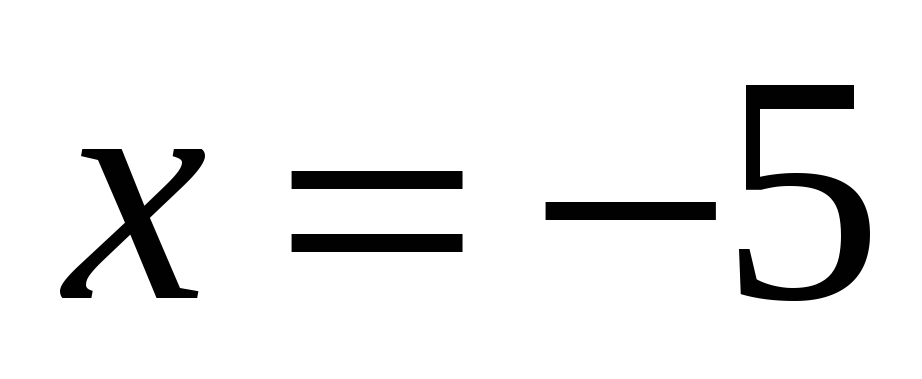 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
На одной полке
 книг, на второй полке на 25 книг меньше.
Книг на двух полках вместе равно: 1)
книг, на второй полке на 25 книг меньше.
Книг на двух полках вместе равно: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
.
Вариант 2
-
Значение выражения
 при
при
 ,
,
 равно: 1) 3; 2)
равно: 1) 3; 2)
 ;
3) 9; 4)
;
3) 9; 4)
 .
. -
Выражение
 после приведения подобных слагаемых
будет равно: 1)
после приведения подобных слагаемых
будет равно: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Разность выражений
 и
и
 равна: 1)
равна: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Выражение
 после упрощения будет равно: 1)
после упрощения будет равно: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Выражение
 не имеет смысла при: 1)
не имеет смысла при: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Прямоугольник имеет ширину
 и длину, которая в 3 раза больше ширины.
Площадь прямоугольника равна: 1)
и длину, которая в 3 раза больше ширины.
Площадь прямоугольника равна: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
.
Тест 3
Определение степени с натуральным и нулевым показателем (п. 6)
Вариант 1
-
Произведение
 можно представить в виде степени так:
1) 7; 2)
можно представить в виде степени так:
1) 7; 2)
 ;
3)
;
3)
 ;
4)
;
4)
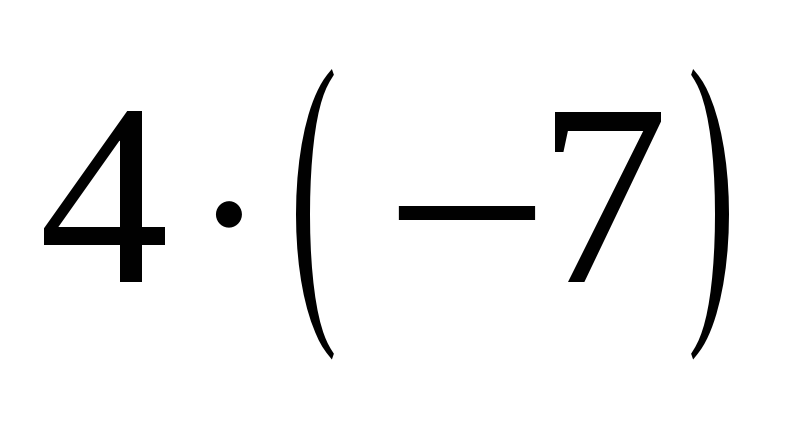 .
. -
Основание степени равно 3, показатель степени равен 4. Значение этой степени равно: 1) 64; 2) 12; 3) 81; 4) 27.
-
Произведение
 в виде степени можно записать так: 1)
в виде степени можно записать так: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Значение степени
 равно: 1)
равно: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Значение числового выражения
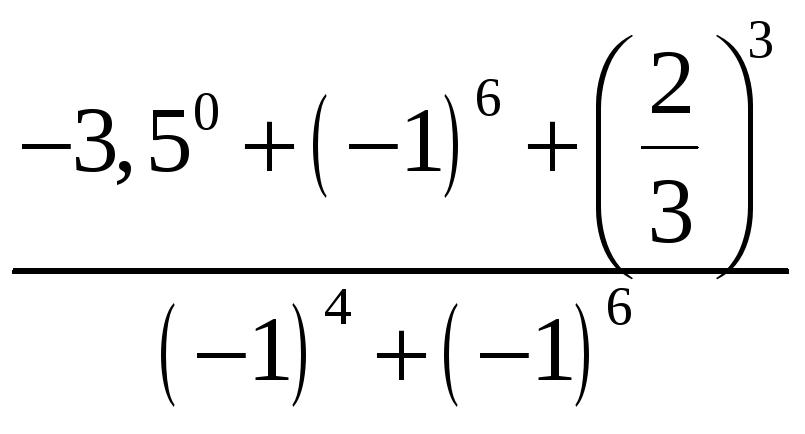 равно: 1)
равно: 1)
 ;
2)
;
2)
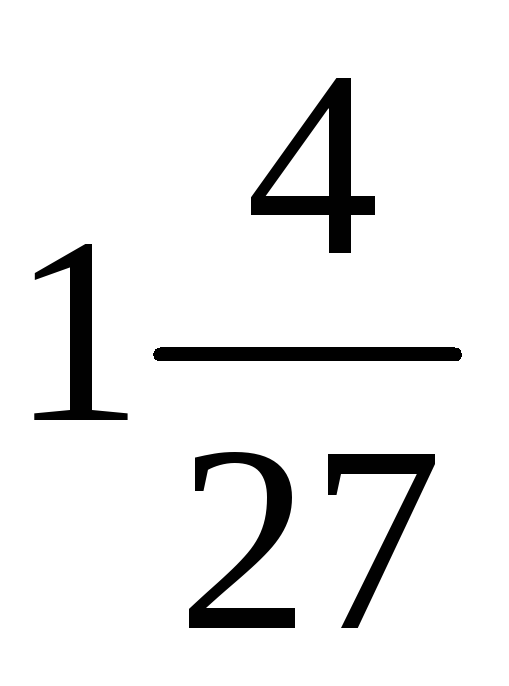 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Число 64 можно записать в виде степени с основанием 4 так: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
.
Вариант 2
-
Произведение
 можно представить в виде степени так:
1) 5; 2)
можно представить в виде степени так:
1) 5; 2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Основание степени равно 2, показатель степени равен 6. Значение этой степени равно: 1) 12; 2) 36; 3) 32; 4) 64.
-
Произведение
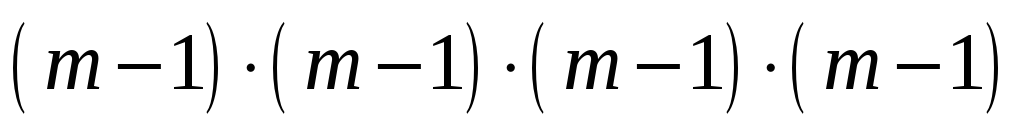 в виде степени можно записать так: 1)
в виде степени можно записать так: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Значение степени
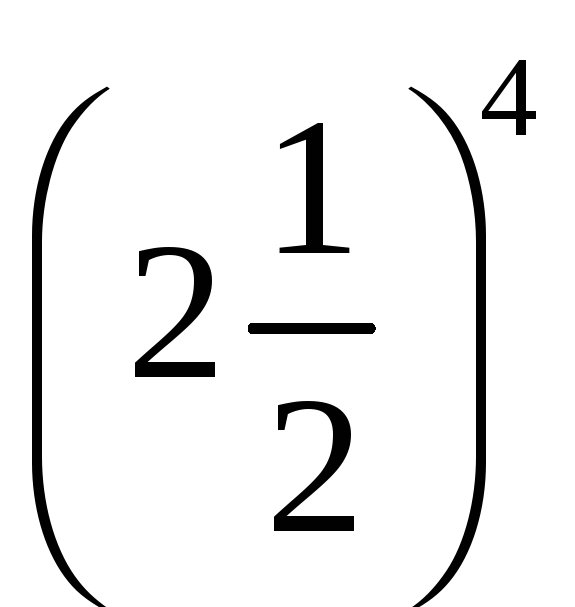 равно: 1)
равно: 1)
 ;
2) 10; 3)
;
2) 10; 3)
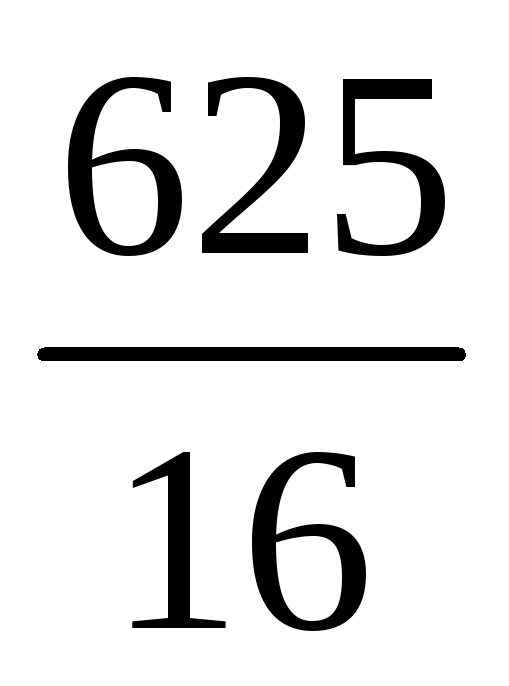 ;
4)
;
4)
 .
. -
Значение числового выражения
 равно: 1)
равно: 1)
 ;
2) 8; 3)
;
2) 8; 3)
 ;
4)
;
4)
 .
. -
Число 10000 можно записать в виде степени с основанием 10 так: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
.
Тест 4
Свойства степени с натуральным и нулевым показателем (п. 7 – 9)
Вариант 1
-
Упростив выражения
 ,
,
 ,
,
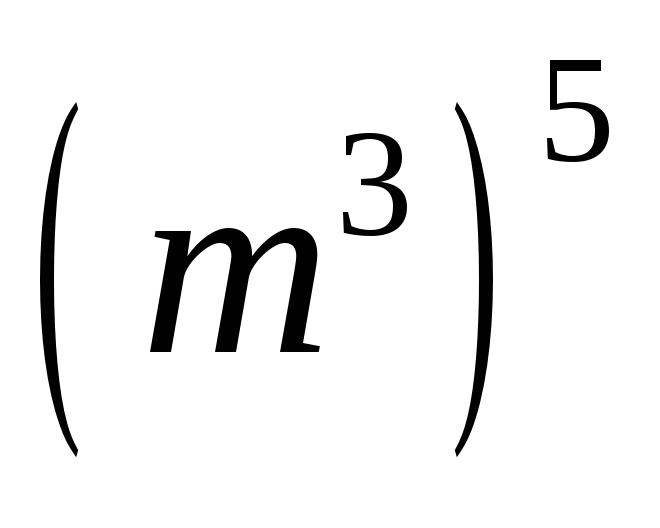 ,
получим: 1)
,
получим: 1)
 ,
,
 ,
,
 ;
2)
;
2)
 ,
,
 ,
,
 ;
3)
;
3)
 ,
,
 ,
,
 ;
4)
;
4)
 ,
,
 ,
,
 .
. -
Значение выражения
 равно: 1) 27; 2) 3; 3) 81; 4) 9.
равно: 1) 27; 2) 3; 3) 81; 4) 9. -
Значение выражения
 равно: 1) 15; 2) 5; 3) 25; 4)
равно: 1) 15; 2) 5; 3) 25; 4)
 .
. -
Степень
 равна: 1)
равна: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Если
 ,
,
 ,
,
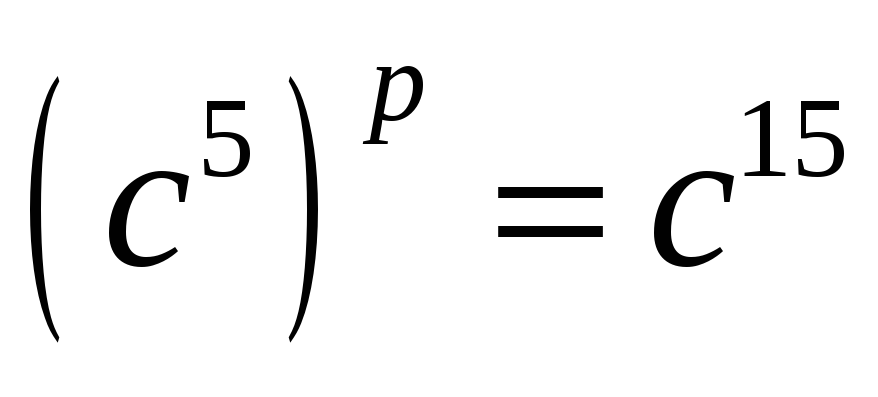 ,
то: 1)
,
то: 1)
 ,
,
 ,
,
 ;
2)
;
2)
 ,
,
 ,
,
 ;
3)
;
3)
 ,
,
 ,
,
 ;
4)
;
4)
 ,
,
 ,
,
 .
. -
Если
 ,
то значение выражения
,
то значение выражения
 равно: 1) 125; 2) 75; 3) 100; 4) 600.
равно: 1) 125; 2) 75; 3) 100; 4) 600.
Вариант 2
-
Упростив выражения
 ,
,
 ,
,
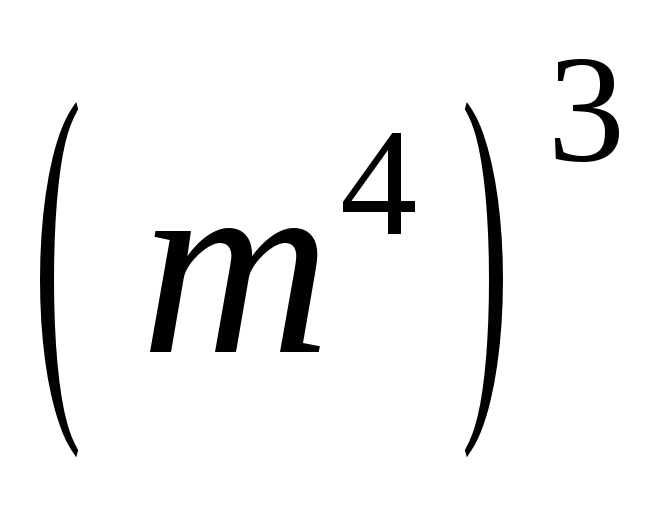 ,
получим: 1)
,
получим: 1)
 ,
,
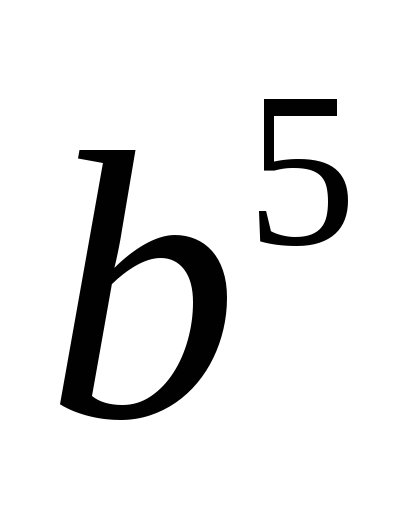 ,
,
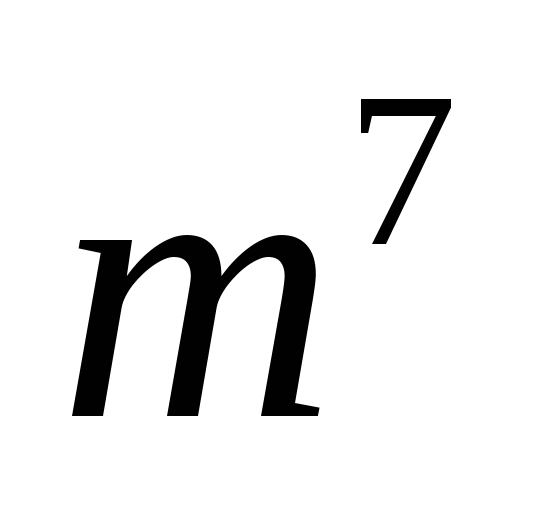 ;
2)
;
2)
 ,
,
 ,
,
 ;
3)
;
3)
 ,
,
 ,
,
 ;
4)
;
4)
 ,
,
 ,
,
 .
. -
Значение выражения
 равно: 1) 7; 2) 49; 3)
равно: 1) 7; 2) 49; 3)
 ;
4)
;
4)
 .
. -
Значение выражения
 равно: 1)
равно: 1)
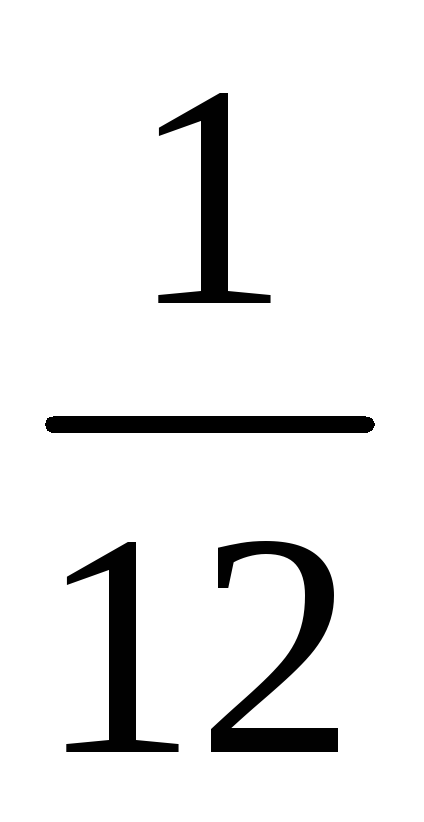 ;
2) 3; 3) 12; 4)
;
2) 3; 3) 12; 4)
 .
. -
Степень
 равна: 1)
равна: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Если
 ,
,
 ,
,
 ,
то: 1)
,
то: 1)
 ,
,
 ,
,
 ;
2)
;
2)
 ,
,
 ,
,
 ;
3)
;
3)
 ,
,
 ,
,
 ;
4)
;
4)
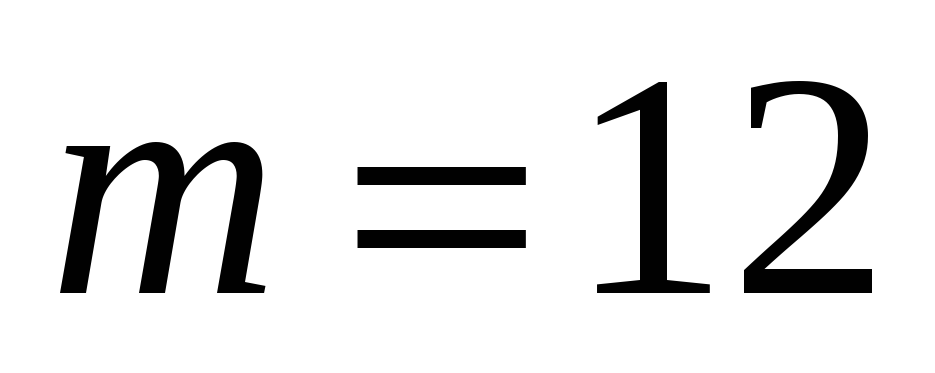 ,
,
 ,
,
 .
. -
Если
 ,
то значение выражения
,
то значение выражения
 равно: 1) 49; 2) 60; 3) 18; 4) 25.
равно: 1) 49; 2) 60; 3) 18; 4) 25.
Тест 5
Одночлен, сложение, умножение и возведение одночленов в степень (п. 8 – 9)
Вариант 1
-
Запись одночлена
 в
стандартном виде такова: 1)
в
стандартном виде такова: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Значение одночлена
 при
при
 ,
,
 равно: 1)
равно: 1)
 ;
2)
;
2)
 ;
3) 8; 4)
;
3) 8; 4)
 .
. -
Произведение одночленов
 и
и
 равно: 1)
равно: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Квадрат одночлена
 равен: 1)
равен: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Одночлен
 равен произведению одночленов
равен произведению одночленов
 и: 1)
и: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Если
 ,
то
,
то
 равно: 1)
равно: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
.
Вариант 2
-
Запись одночлена
 в стандартном виде такова: 1)
в стандартном виде такова: 1)
 ;
2)
;
2)
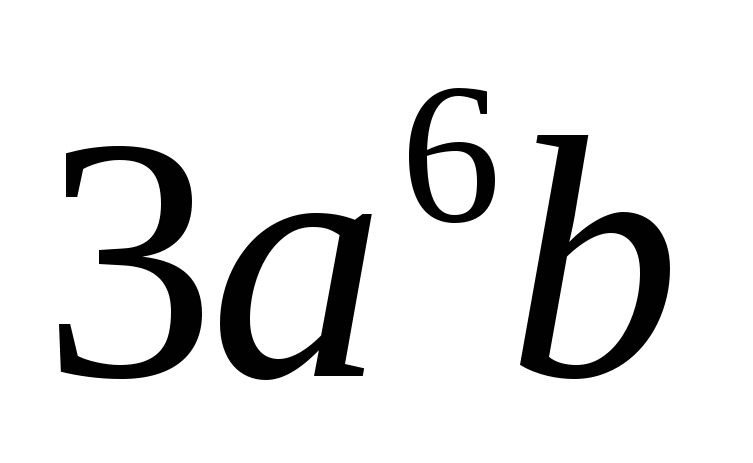 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Значение одночлена
 при
при
 ,
,
 равно: 1) 21; 2)
равно: 1) 21; 2)
 ;
3) 10,5; 4)
;
3) 10,5; 4)
 .
. -
Произведение одночленов
 и
и
 равно: 1)
равно: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Квадрат одночлена
 равен: 1)
равен: 1)
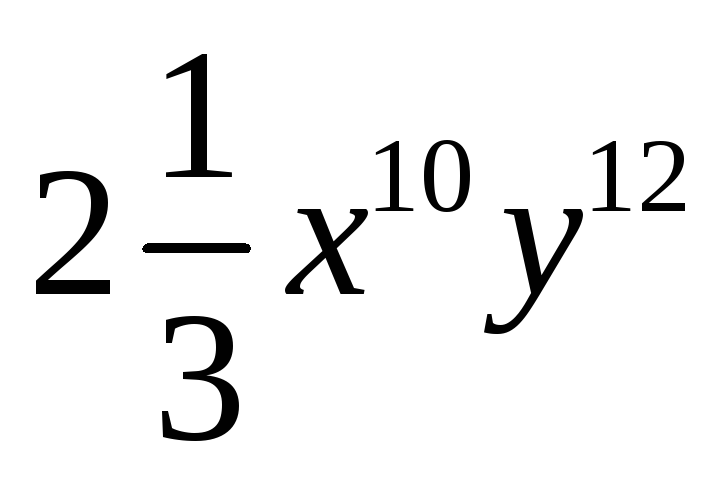 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Одночлен
 равен произведению одночленов
равен произведению одночленов
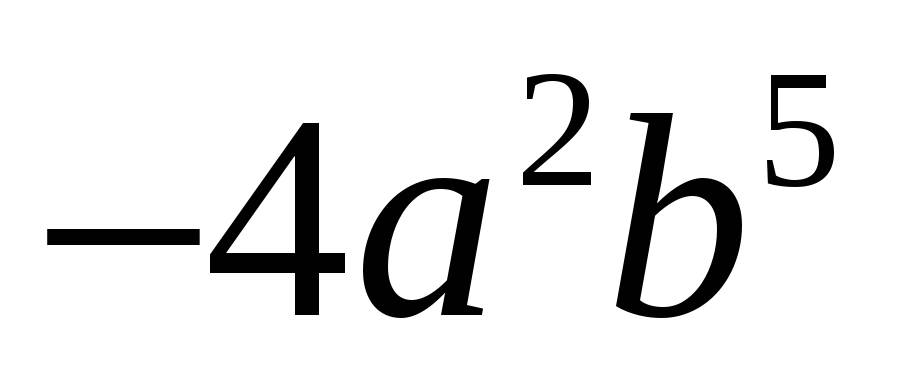 и: 1)
и: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Если
 ,
то
,
то
 равно: 1) 20; 2)
равно: 1) 20; 2)
 ;
3)
;
3)
 ;
4) 18.
;
4) 18.
Тест 6
Многочлен и его стандартный вид, сумма и разность многочленов (п. 11 – 13)
Вариант 1
-
Многочлен
 в стандартном виде записывается так:
1)
в стандартном виде записывается так:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Сумма многочленов
 и
и
 равна: 1)
равна: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Разность многочленов
 и
и
 равна: 1)
равна: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Значение многочлена
 при
при
 ,
,
 равно: 1)
равно: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
. -
Выражение
 равно: 1)
равно: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4) 7.
;
4) 7. -
Степень многочлена
 равна: 1) 1; 2) 2; 3) 3; 4) 4.
равна: 1) 1; 2) 2; 3) 3; 4) 4.
