Вариант 2

1. Представьте в виде суммы одночленов произведение многочленов: а) ; б); в).

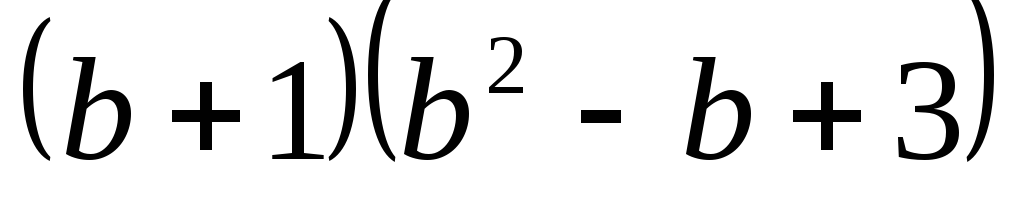2. Упростите: а) ; б).

3. Одно из двух натуральных чисел при делении на 7 дает остаток 5, а другое – остаток 3. Какой остаток получится при делении произведения этих чисел на 7?

4. Упростите выражение и найдите его значение при.

5. При каком значении переменной p многочлен, тождественно равный произведению : а) имеет коэффициент при, равный; б) имеет коэффициент при, равный нулю?

6. Упростите выражение , выполнив удобную замену переменных.

7. Представьте степень в виде произведения и упростите.

Вариант 3

1. Представьте в виде суммы одночленов произведение многочленов: а) ; б); в).

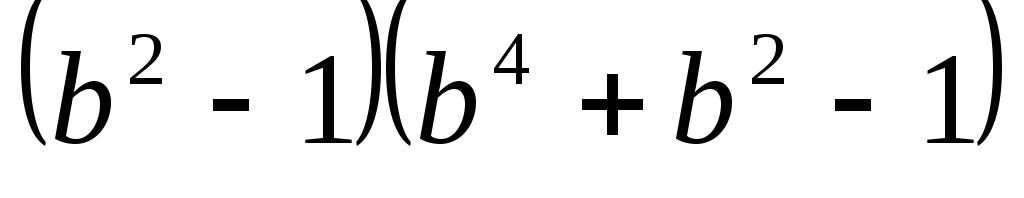2. Упростите: а) ; б).

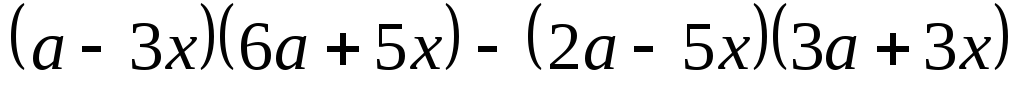3. Одно из двух натуральных чисел при делении на 17 дает остаток 15, а другое – остаток 13. Какой остаток получится при делении произведения этих чисел на 17?

4. Упростите выражение и найдите его значение при,.

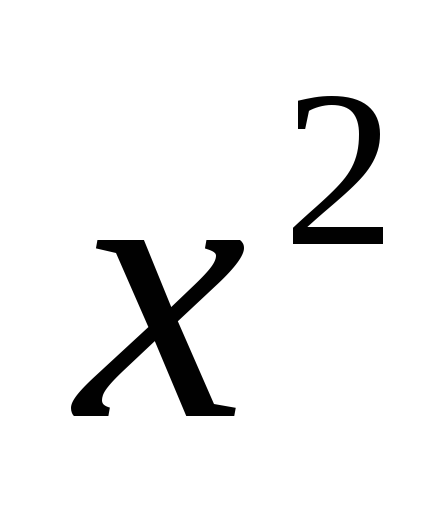5. При каком значении переменной p многочлен, тождественно равный произведению : а) имеет коэффициент при, равный; б) имеет сумму коэффициентов, равную нулю?

6. Упростите выражение , выполнив удобную замену переменных.

7. Докажите, что выражение тождественно равно выражению.

Самостоятельная работа № 9

§ 7. Уравнение с одной переменной Основные сведения Равенство, содержащее переменную, называется уравнением с одной переменой или уравнением с одним неизвестным.

Корнем уравнения (решением уравнения) называется значение переменной, при котором уравнение обращается в верное числовое равенство. Решить уравнение – значит найти множество его корней.

Областью определения уравнения с одной переменной (областью допустимых значений переменной, входящей в уравнение) называется множество значений переменной, при которых обе части уравнения имеют смысл.

Уравнения называются равносильными, если множества их корней совпадают. Уравнения, не имеющие корней, являются равносильными. Иногда при переходе от одного уравнения к другому, ему равносильному, используется знак .

Из данного уравнения получается равносильное ему уравнение, если:

1. перенести слагаемое из одной части уравнения в другую, изменив его знак;

2. обе части уравнения умножить или разделить на одно и то же отличное от нуля число;

3. в какой-либо части или в обеих частях уравнения выполнить тождественное преобразование, не меняющее области определения уравнения.

Уравнение вида , где– переменная,и– некоторые числа, называетсялинейным уравнением с одной переменной. Множество корней линейного уравнения может состоять из одного элемента (при ), быть пустым множеством (прии), быть бесконечным множеством (прии).

Подготовительный вариант

1. Является ли число корнем уравнения: а),; б),?

2. Даны уравнения (А),(Б),(В) и(Г). Укажите те, которые равносильны уравнению. Ответ объясните.

3. Решите уравнение: а) ; б); в); г).

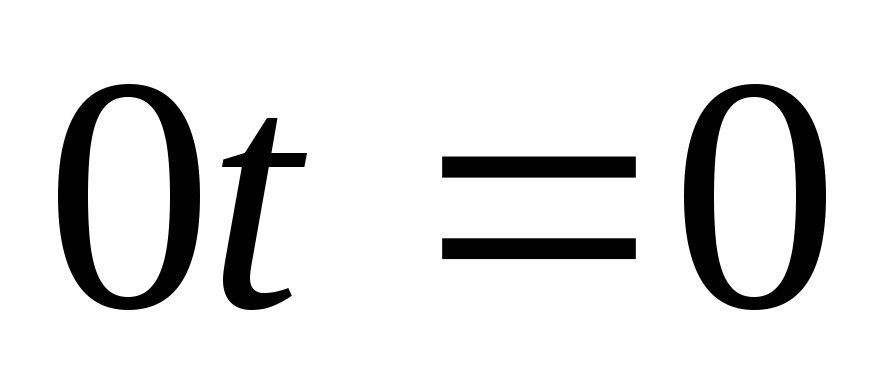4. Найдите все целые значения параметра , при которых уравнениеимеет целый корень.

5. Найдите множество корней уравнения: а) ; б); в); г).

6. При каких значениях параметра уравнение: а) имеет единственный корень; б) не имеет корней; в) имеет бесконечное множество корней?

7. Решите уравнение (и) относительно переменной: а); б).

8. Дано уравнение . Проверьте, являются ли его корнями числа: а) 1; б); в) 2; г); д) 4; е)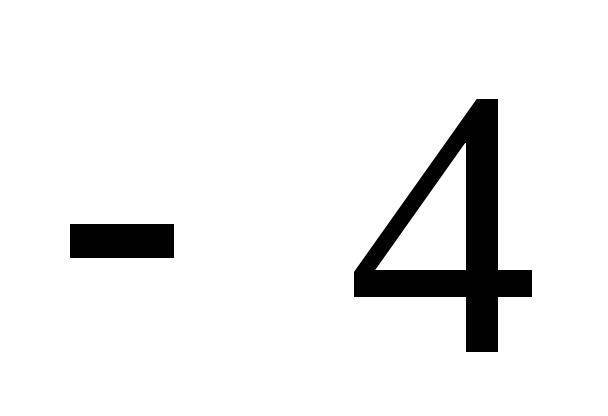.