
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 1. Множества Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 2. Числовые выражения и выражения с переменными Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 3. Степень с натуральным показателем Основные сведения
- •Подготовительный вариант
- •Подготовительный вариант
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 6. Сумма, разность и произведение многочленов Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 6. Сумма, разность и произведение многочленов Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 7. Уравнение с одной переменной Основные сведения Равенство, содержащее переменную, называется уравнением с одной переменой или уравнением с одним неизвестным.
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 8. Решение уравнений и задач Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 9. Способы разложения многочленов на множители
- •Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 10. Применение разложения многочлена на множители
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 12. Квадрат суммы и квадрат разности
- •§ 13. Куб суммы и куб разности, сумма и разность кубов Основные сведения
- •Подготовительный вариант
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 15. Линейная функция Основные сведения
- •Если угловые коэффициенты прямых, являющихся графиками линейных функций, различны, то прямые пересекаются, если угловые коэффициенты прямых равны, то прямые параллельны. Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 17. Линейные уравнения с двумя переменными Основные сведения Равенство, содержащее выражения с двумя переменными, называется уравнением с двумя переменными.
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 18. Системы линейных уравнений и способы их решения
- •Вариант 1
- •Вариант 2
- •Вариант 3
Вариант 1
Даны многочлены
 и
и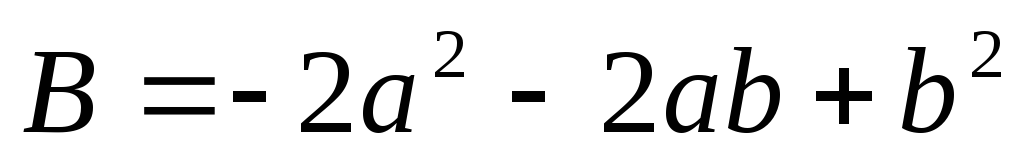 .
Найдите: а)
.
Найдите: а) ;
б)
;
б) .
.Упростите выражение: а)
 ;
б)
;
б) .
.Представьте выражение
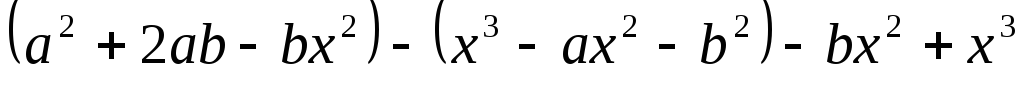 в виде суммы двух многочленов, один из
которых содержит переменную
в виде суммы двух многочленов, один из
которых содержит переменную ,
а другой – не содержит.
,
а другой – не содержит.Представьте многочлен
 в виде разности двух многочленов с
положительными коэффициентами.
в виде разности двух многочленов с
положительными коэффициентами.Вместо знака
 запишите такой одночлен, чтобы многочлен,
тождественно равный выражению
запишите такой одночлен, чтобы многочлен,
тождественно равный выражению ,
был многочленом 5-ой степени, сумма
коэффициентов которого равна 8.
,
был многочленом 5-ой степени, сумма
коэффициентов которого равна 8.Упростите выражение и найдите его значение: а)
 при
при ,
,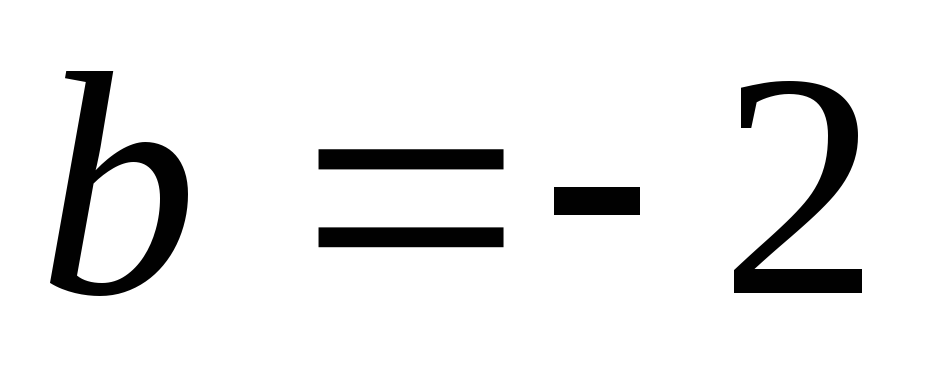 ;
б)
;
б)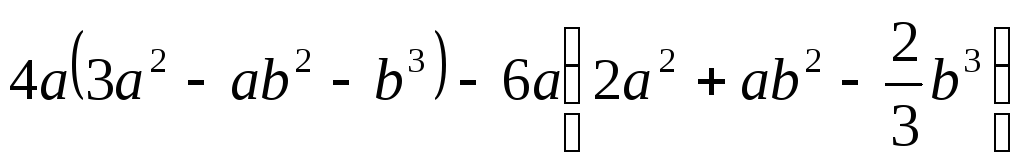 при
при ,
, .
.Упростите выражение
 и найдите, при каком значении переменной
и найдите, при каком значении переменной
 его значение равно нулю.
его значение равно нулю.Сравните числа
 и
и .
Укажите какое-нибудь число (если оно
существует), заключенное между этими
числами.
.
Укажите какое-нибудь число (если оно
существует), заключенное между этими
числами.
Вариант 2
Даны многочлены
 и
и .
Найдите: а)
.
Найдите: а) ;
б)
;
б) .
.Упростите выражение: а)
 ;
б)
;
б) .
.Представьте выражение
 в виде суммы двух многочленов, один из
которых содержит переменную
в виде суммы двух многочленов, один из
которых содержит переменную ,
а другой – не содержит.
,
а другой – не содержит.Представьте многочлен
 в виде разности двух многочленов с
положительными коэффициентами.
в виде разности двух многочленов с
положительными коэффициентами.Вместо знака
 запишите такой одночлен, чтобы многочлен,
тождественно равный выражению
запишите такой одночлен, чтобы многочлен,
тождественно равный выражению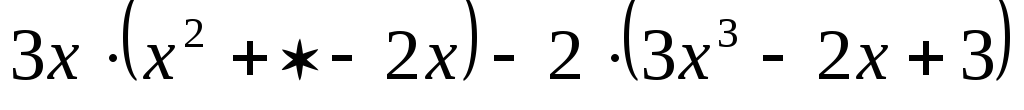 ,
был многочленом 4-ой степени, сумма
коэффициентов которого равна 4.
,
был многочленом 4-ой степени, сумма
коэффициентов которого равна 4.Упростите выражение и найдите его значение: а)
 при
при ,
, ;
б)
;
б) при
при ,
, .
.Упростите выражение
 и найдите, при каком значении переменной
и найдите, при каком значении переменной
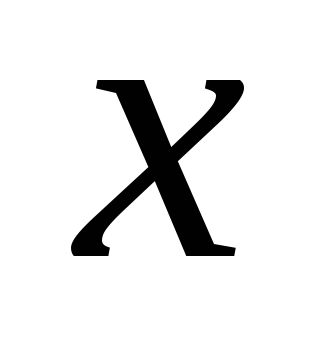 его значение равно нулю.
его значение равно нулю.Сравните числа
 и
и .
Укажите какое-нибудь число (если оно
существует), заключенное между этими
числами.
.
Укажите какое-нибудь число (если оно
существует), заключенное между этими
числами.
Вариант 3
Даны многочлены
 и
и .
Найдите: а)
.
Найдите: а) ;
б)
;
б) .
.Упростите выражение: а)
 ;
б)
;
б) .
.Представьте выражение
 в виде суммы двух многочленов, один из
которых содержит переменную
в виде суммы двух многочленов, один из
которых содержит переменную ,
а другой – не содержит.
,
а другой – не содержит.Представьте многочлен
 в виде разности двух многочленов с
положительными коэффициентами.
в виде разности двух многочленов с
положительными коэффициентами.Вместо знака
 запишите такой одночлен, чтобы многочлен,
тождественно равный выражению
запишите такой одночлен, чтобы многочлен,
тождественно равный выражению ,
был многочленом 4-ой степени, сумма
коэффициентов которого равна нулю.
,
был многочленом 4-ой степени, сумма
коэффициентов которого равна нулю.Упростите выражение и найдите его значение: а)
 при
при ,
, ;
б)
;
б) при
при ,
, .
.Упростите выражение
 и найдите, при каком значении переменной
и найдите, при каком значении переменной
 его значение равно нулю.
его значение равно нулю.Сравните числа
 и
и .
Укажите какое-нибудь число (если оно
существует), заключенное между этими
числами.
.
Укажите какое-нибудь число (если оно
существует), заключенное между этими
числами.
Самостоятельная работа № 8
§ 6. Сумма, разность и произведение многочленов Подготовительный вариант
Представьте в виде суммы одночленов произведение многочленов: а)
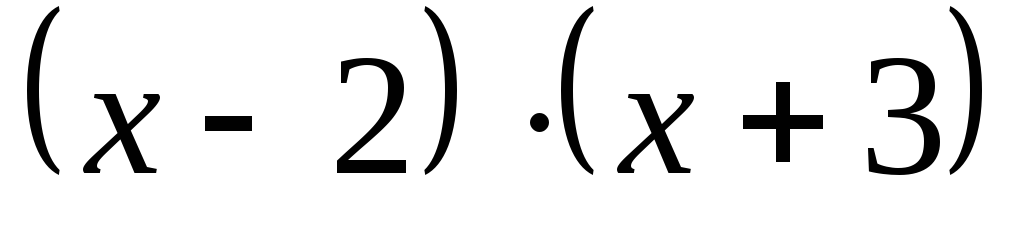 ;
б)
;
б) ;
в)
;
в)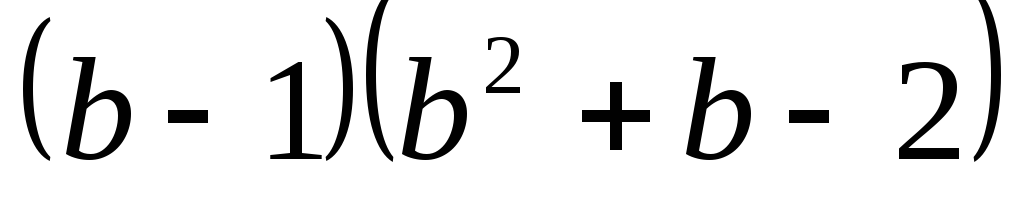 .
.Упростите: а)
 ;
б)
;
б) .
.Одно из двух натуральных чисел при делении на 13 дает остаток 7, а другое – остаток 2. Какой остаток получится при делении произведения этих чисел на 13?
Упростите выражение
 и найдите его значение при
и найдите его значение при .
.При каком значении переменной p многочлен, тождественно равный произведению
 :
а) имеет коэффициент при
:
а) имеет коэффициент при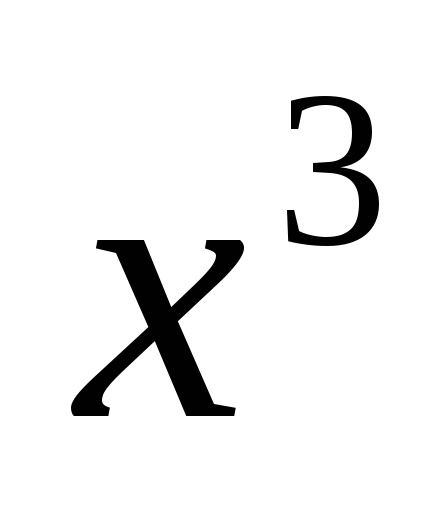 ,
равный
,
равный ;
б) имеет коэффициент при
;
б) имеет коэффициент при ,
равный нулю?
,
равный нулю?Упростите выражение
 ,
выполнив удобную замену переменных.
,
выполнив удобную замену переменных.Докажите что выражение
 тождественно равно выражению
тождественно равно выражению .
.
Вариант 1
Представьте в виде суммы одночленов произведение многочленов: а)
 ;
б)
;
б) ;
в)
;
в) .
.Упростите: а)
 ;
б)
;
б)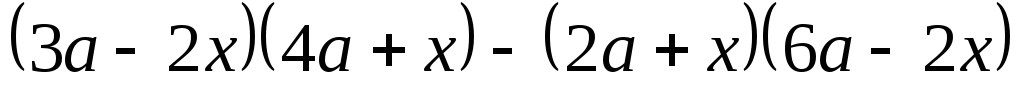 .
.Одно из двух натуральных чисел при делении на 5 дает остаток 2, а другое – остаток 3. Какой остаток получится при делении произведения этих чисел на 5?
Упростите выражение
 и найдите его значение при
и найдите его значение при .
.При каком значении переменной p многочлен, тождественно равный произведению
 :
а) имеет коэффициент при
:
а) имеет коэффициент при ,
равный
,
равный ;
б) имеет коэффициент при
;
б) имеет коэффициент при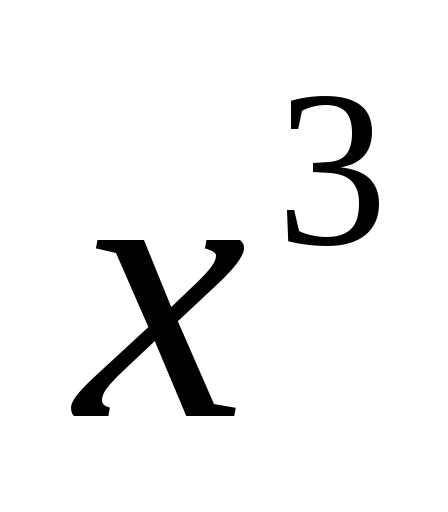 ,
равный нулю?
,
равный нулю?Упростите выражение
 ,
выполнив удобную замену переменных.
,
выполнив удобную замену переменных.Представьте степень
 в виде произведения и упростите.
в виде произведения и упростите.
