
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 1. Множества Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 2. Числовые выражения и выражения с переменными Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 3. Степень с натуральным показателем Основные сведения
- •Подготовительный вариант
- •Подготовительный вариант
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 6. Сумма, разность и произведение многочленов Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 6. Сумма, разность и произведение многочленов Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 7. Уравнение с одной переменной Основные сведения Равенство, содержащее переменную, называется уравнением с одной переменой или уравнением с одним неизвестным.
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 8. Решение уравнений и задач Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 9. Способы разложения многочленов на множители
- •Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 10. Применение разложения многочлена на множители
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 12. Квадрат суммы и квадрат разности
- •§ 13. Куб суммы и куб разности, сумма и разность кубов Основные сведения
- •Подготовительный вариант
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 15. Линейная функция Основные сведения
- •Если угловые коэффициенты прямых, являющихся графиками линейных функций, различны, то прямые пересекаются, если угловые коэффициенты прямых равны, то прямые параллельны. Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 17. Линейные уравнения с двумя переменными Основные сведения Равенство, содержащее выражения с двумя переменными, называется уравнением с двумя переменными.
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 18. Системы линейных уравнений и способы их решения
- •Вариант 1
- •Вариант 2
- •Вариант 3
Подготовительный вариант
Вычислите значение выражения: а)
 ;
б)
;
б) .
.Упростите выражение при всех
 :
а)
:
а) ;
б)
;
б) .
.Найдите значение выражения
 ,
если
,
если .
.Найдите все значения x, при которых верно равенство: а)
 ;
б)
;
б) ;
в)
;
в) ?
?Найдите множество значений выражения при

 .
.Заполните таблицу значений выражения
 при
при ,
, .
.Пусть
 ,
,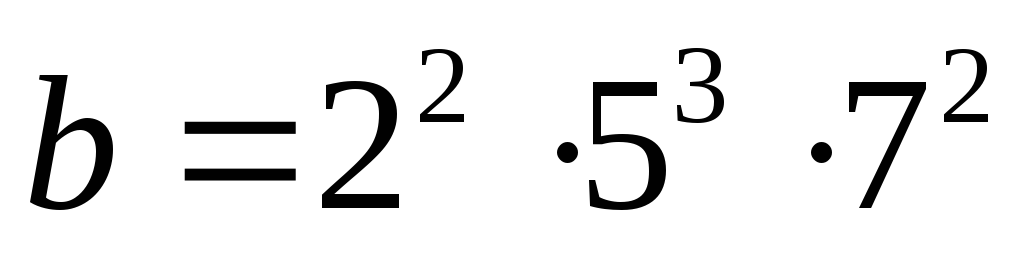 .
Найдите наибольший общий делитель и
наименьшее общее кратное чисела
и b.
.
Найдите наибольший общий делитель и
наименьшее общее кратное чисела
и b.
Вариант 1
Вычислите значение выражения: а)
 ;
б)
;
б) .
.Упростите выражение при всех
 :
а)
:
а)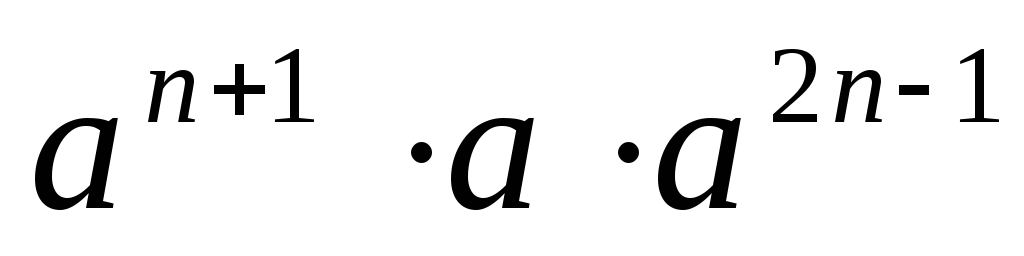 ;
б)
;
б) .
.Найдите значение выражения
 при
при .
.При каком значении x верно равенство: а)
 ;
б)
;
б) ;
в)
;
в) ?
?Найдите множество значений выражения при

 .
.Заполните таблицу значений выражения
 при
при ,
, .
.Пусть
 ,
, .
Найдите наибольший общий делитель и
наименьшее общее кратное чисела
и b.
.
Найдите наибольший общий делитель и
наименьшее общее кратное чисела
и b.
Вариант 2
Вычислите: а)
 ;
б)
;
б) .
.Упростите выражение при всех
 :
а)
:
а) ;
б)
;
б) .
.Найдите значение выражения
 при
при .
.При каком значении x верно равенство: а)
 ;
б)
;
б) ;
в)
;
в) ?
?Найдите множество значений выражения при

 .
.Заполните таблицу значений выражения
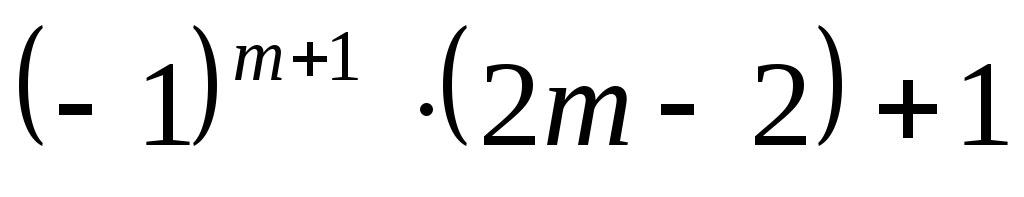 при
при ,
, .
.Пусть
 ,
, .
Найдите наибольший общий делитель и
наименьшее общее кратное чисела
и b.
.
Найдите наибольший общий делитель и
наименьшее общее кратное чисела
и b.
Вариант 3
Вычислите значение выражения: а)
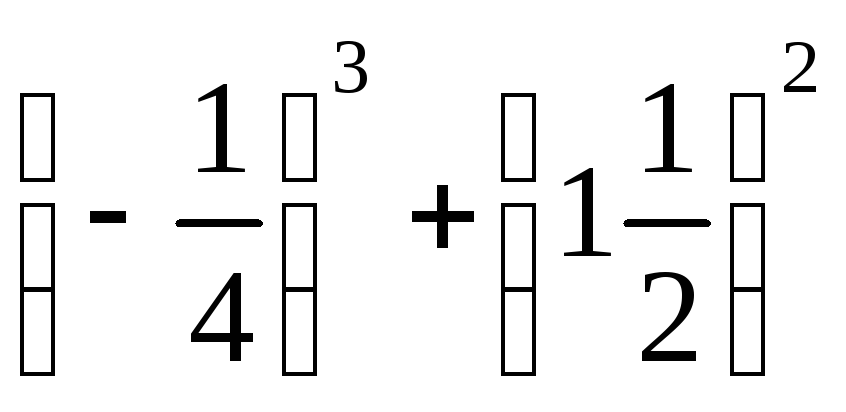 ;
б)
;
б) .
.Упростите выражение при всех
 :
а)
:
а) ;
б)
;
б) .
.Найдите значение выражения
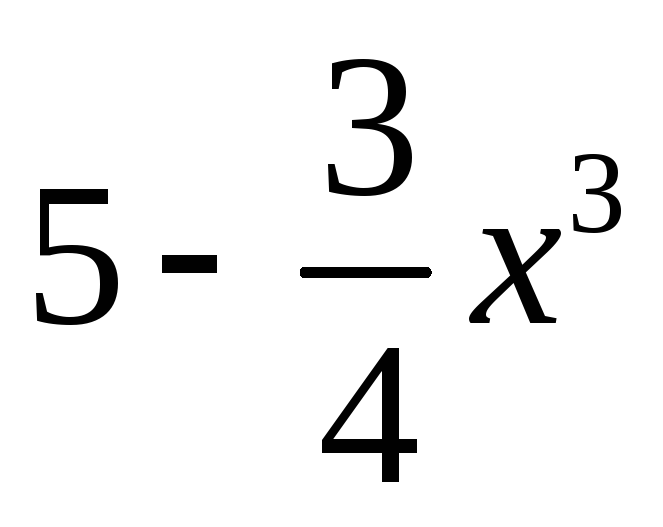 ,
если
,
если .
.Найдите все значения x, при которых верно равенство: а)
 ;
б)
;
б) ;
в)
;
в) ?
?Найдите множество значений выражения при

 .
.Заполните таблицу значений выражения
 при
при ,
, .
.Пусть
 ,
, .
Найдите наибольший общий делитель и
наименьшее общее кратное чисела
и b.
.
Найдите наибольший общий делитель и
наименьшее общее кратное чисела
и b.
Самостоятельная работа № 5
§ 4. Одночлен и его стандартный вид
Основные сведения
Выражения, представляющие собой произведение чисел, переменных и их степеней, называют одночленами.
Одночлен, записанный в виде произведения числового множителя, стоящего на первом месте, и степеней различных переменных, записанных в алфавитном порядке, называется стандартным видом одночлена. Числовой множитель в этом случае называется коэффициентом одночлена.
Степенью одночлена стандартного вида называют сумму показателей степеней входящих в него переменных.
Свойства степени с натуральным показателем
Если
![]() и
и![]() – произвольные числа,
– произвольные числа,![]() – натуральное число, то
– натуральное число, то![]() .
.
Если
![]() – произвольное число,
– произвольное число,![]() и
и![]() – натуральные числа, то
– натуральные числа, то![]() .
.
Если
![]() и
и![]() – произвольные числа, где
– произвольные числа, где![]() ,
,![]() – натуральное число, то
– натуральное число, то![]() .
.
Тождество – это равенство, верное при любых допустимых значениях входящих в него переменных. Выражения, соответственные значения которых равны при любых допустимых значениях переменных, называются тождественно равными. Замена одного выражения другим, тождественно равным ему, называется тождественным преобразованием.
Подготовительный вариант
Запишите одночлен
 в стандартном виде и укажите его степень.
в стандартном виде и укажите его степень.Выполните умножение одночленов: а)
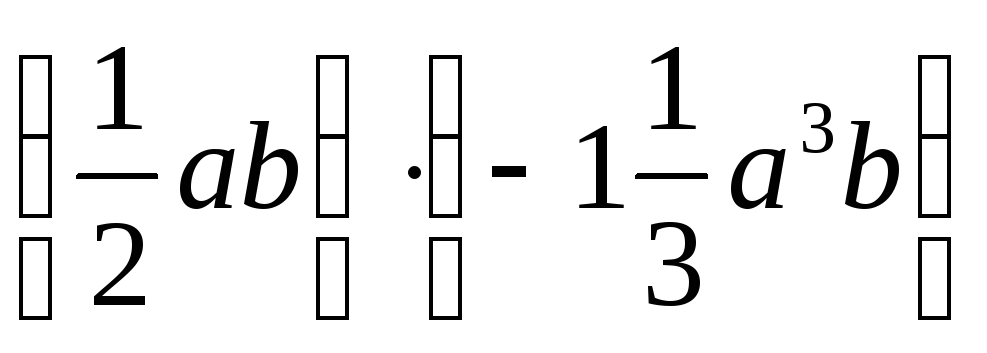 ;
б)
;
б) .
.Возведите одночлен в степень: а)
 ;
б)
;
б) ;
в)
;
в)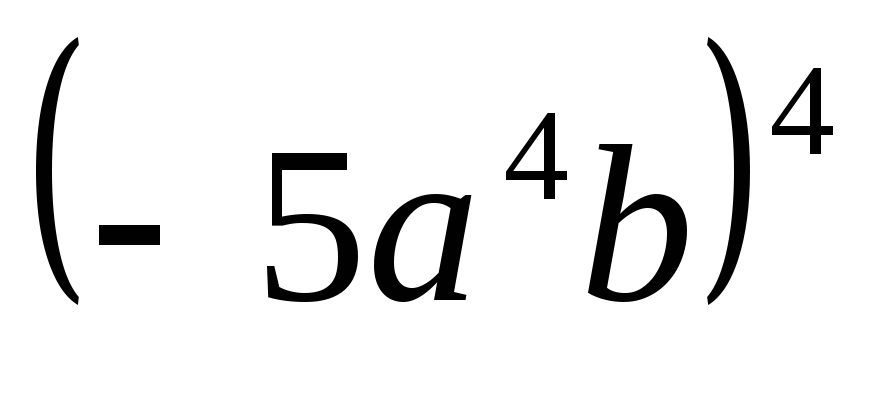 .
.Упростите выражение: а)
 ;
б)
;
б) .
.Вычислите значение выражения: а)
 ;
б)
;
б) ;
в)
;
в) .
.Решите уравнение
 .
.Докажите, что значение выражения
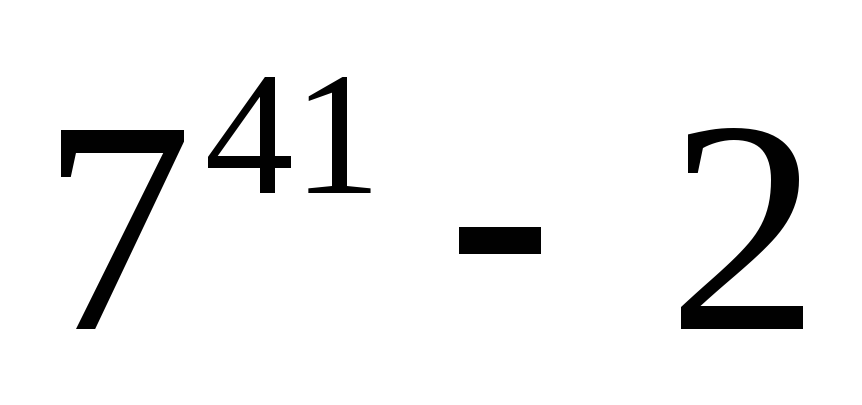 кратно 5.
кратно 5.
Вариант 1
Запишите одночлен
 в стандартном виде и укажите его степень.
в стандартном виде и укажите его степень.Выполните умножение одночленов: а)
 ;
б)
;
б) .
.Возведите одночлен в степень: а)
 ;
б)
;
б) ;
в)
;
в) .
.Упростите выражение: а)
 ;
б)
;
б) .
.Вычислите значение выражения: а)
 ;
б)
;
б) .
.Решите уравнение
 .
.Докажите, что значение выражения
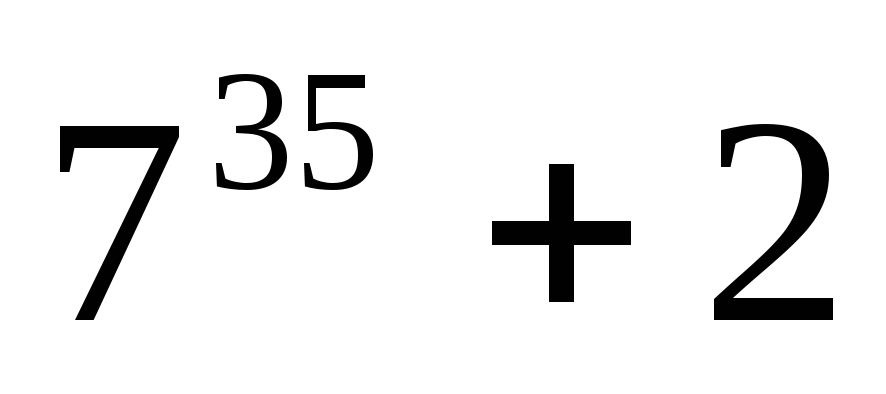 кратно 5.
кратно 5.
Вариант 2
Запишите одночлен
 в стандартном виде и укажите его степень.
в стандартном виде и укажите его степень.Выполните умножение одночленов: а)
 ;
б)
;
б)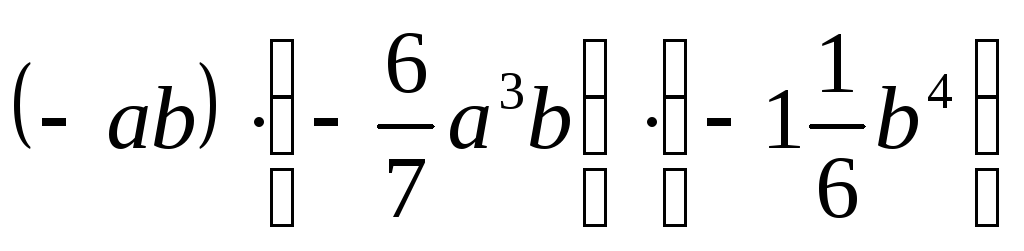 .
.Возведите одночлен в степень: а)
 ;
б)
;
б) ;
в)
;
в) .
.Упростите выражение: а)
 ;
б)
;
б) .
.Вычислите значение выражения: а)
 ;
б)
;
б) .
.Решите уравнение
 .
.Докажите, что значение выражения
 кратно 5.
кратно 5.
Вариант 3
Запишите одночлен
 в стандартном виде и укажите его степень.
в стандартном виде и укажите его степень.Выполните умножение одночленов: а)
 ;
б)
;
б) .
.Возведите одночлен в степень: а)
 ;
б)
;
б) ;
в)
;
в) .
.Упростите выражение: а)
 ;
б)
;
б) .
.Вычислите значение выражения: а)
 ;
б)
;
б) .
.Решите уравнение
 .
.Докажите, что значение выражения
 кратно 10.
кратно 10.
Самостоятельная работа № 6
§ 5. Многочлен и его стандартный вид
Основные сведения
Многочленом называется сумма одночленов. Одночлены, из которых составлен многочлен, называются членами многочлена. Многочлен, составленный из двух одночленов, называется двучленом (биномом), из трех одночленов – трехчленом. Одночлен считают многочленом, состоящим из одного члена (мономом).
Члены многочлена, имеющие одинаковую буквенную часть, называются подобными. Слагаемые, не имеющие буквенной части, также считаются подобными. Замена суммы подобных членов многочлена одночленом называется приведением подобных членов или приведением подобных слагаемых.
Многочлен, составленный из одночленов стандартного вида, среди которых нет подобных членов, называют многочленом стандартного вида.
Степенью многочлена стандартного вида называется наибольшая степень входящих в него одночленов. Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.
Если многочлен является числом, отличным от нуля, то степень такого многочлена равна 0. Число нуль называют нуль-многочленом. Его степень считается не определенной.
Среди многочленов
выделяют многочлены с одной переменной.
Многочлен
![]() -ой
степени с одной переменной в стандартном
виде записывается так:
-ой
степени с одной переменной в стандартном
виде записывается так:![]() ,
где
,
где![]() – переменная,
– переменная,![]() ,
,![]() ,
,![]() ,
….,
,
….,![]() ,
,![]() – произвольные числа,
– произвольные числа,![]() или
или![]() .
Коэффициент при
.
Коэффициент при![]() ,
называютстаршим
коэффициентом
(в нашем случае, это
,
называютстаршим
коэффициентом
(в нашем случае, это
![]() ).
Слагаемое, не содержащее переменной
).
Слагаемое, не содержащее переменной![]() ,
называютсвободным
членом
многочлена (в нашем случае это
,
называютсвободным
членом
многочлена (в нашем случае это
![]() ).
).
Два многочлена тождественно равны, если в стандартном виде каждого из них содержатся одинаковые одночлены. В частности, многочлены с одной переменной тождественно равны, если коэффициенты при одинаковых степенях переменной равны.
Значение многочлена
с переменной
![]() при
при![]() равно свободному члену этого многочлена,
а при
равно свободному члену этого многочлена,
а при![]() – сумме его коэффициентов.
– сумме его коэффициентов.
