Вариант 1

1. Используя характеристическое свойство, запишите: а) множество A всех натуральных чисел, кратных 8; б) множество B всех натуральных чисел, которые при делении на 8 дают в остатке 1.

2. Найдите значение выражения при.

3. При каких значениях переменной выражение имеет смысл?

4. При каком значении переменной выражение не имеет смысла?

5. Составьте выражение для решения задачи. Моторный катер, собственная скорость которого 10 км/ч, прошел по реке расстояние, равное 25 км, вниз по течению и такое же расстояние вверх по течению. Найдите скорость течения реки, если время, затраченное на весь путь равно 5 ч.

6. Для ряда данных 4; 4; 4; 5; 5 найдите: а) размах; б) объем; в) среднее арифметическое; г) моду; д) медиану.

7. Заполните таблицу значений выражения с шагом 1 для всех целых значений переменной, удовлетворяющих условию.

8. Известно, что . Чему равно значение выражения: а); б); в)?

Вариант 2

1. Используя характеристическое свойство, запишите: а) множество A всех натуральных чисел, кратных 13; б) множество B всех натуральных чисел, которые при делении на 13 дают в остатке 12.

2. Найдите значение выражения при.

3. При каких значениях переменной выражение имеет смысл?

4. При каком значении переменной выражение не имеет смысла?

5. Составьте выражение для решения задачи. Моторная лодка, собственная скорость которой 12 км/ч, прошла по реке расстояние, равное 30 км, вниз по течению и такое же расстояние вверх по течению. Найдите скорость течения реки, если время, затраченное на весь путь равно 6 ч.

6. Для ряда данных 3; 4; 5; 5; 5 найдите: а) размах; б) объем; в) среднее арифметическое; г) моду; д) медиану.

7. Заполните таблицу значений выражения 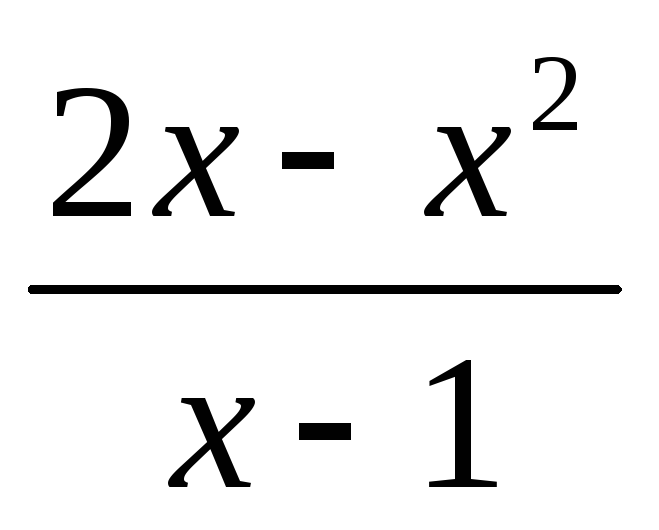с шагом 1 для всех целых значений переменной, удовлетворяющих условию.

8. Известно, что . Чему равно значение выражения: а); б); в)?

Вариант 3

1. Используя характеристическое свойство, запишите: а) множество A всех натуральных чисел, кратных 17; б) множество B всех натуральных чисел, которые при делении на 17 дают в остатке 1.

2. Найдите значение выражения при.

3. При каких значениях переменной выражение имеет смысл?

4. При каких значениях переменной выражение 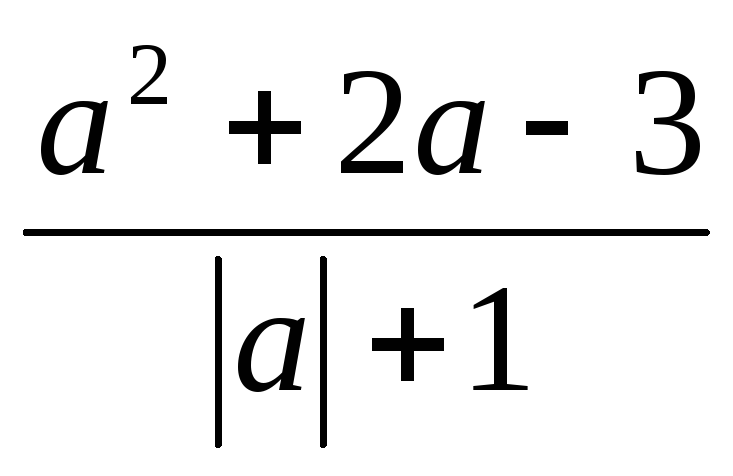не имеет смысла?

5. Составьте уравнение для решения задачи. 17 туристов во время ночевки расположились в двухместных и трехместных палатках. Всего было 7 палаток. Сколько из них было двухместных?

6. Для ряда данных 3; 4; 4; 5; 5 найдите: а) размах; б) объем; в) среднее арифметическое; г) моду; д) медиану

7. Заполните таблицу значений выражения с шагом 1 для всех целых значений переменной, удовлетворяющих условию.

8. Известно, что . Чему равно значение выражения: а); б); в)?

Самостоятельная работа № 4

§ 3. Степень с натуральным показателем Основные сведения

Степенью числа с натуральным показателем , большим 1, называют выражение, равное произведениюмножителей, каждый из которых равен. Степенью числас показателем 1 называют выражение, равное. Степенью числас нулевым показателем называется выражение, равное 1. Выражениене имеет смысла!

В выражении числоназываютоснованием степени, число –показателем степени. Вторую степень числа иногда называют квадратом, третью степень – кубом числа. Нахождение -ой степени числаназываютвозведением в -ю степень.

Свойства степени с натуральным показателем

Очевидно, при .

Если ,или, то.

Если и, гдеили, то.

Если и, гдеили, то.

Если – произвольное число,– натуральные числа, то.

Если – произвольное число,– натуральные числа, причем, то.