
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 1. Множества Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 2. Числовые выражения и выражения с переменными Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 3. Степень с натуральным показателем Основные сведения
- •Подготовительный вариант
- •Подготовительный вариант
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 6. Сумма, разность и произведение многочленов Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 6. Сумма, разность и произведение многочленов Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 7. Уравнение с одной переменной Основные сведения Равенство, содержащее переменную, называется уравнением с одной переменой или уравнением с одним неизвестным.
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 8. Решение уравнений и задач Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 9. Способы разложения многочленов на множители
- •Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 10. Применение разложения многочлена на множители
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 12. Квадрат суммы и квадрат разности
- •§ 13. Куб суммы и куб разности, сумма и разность кубов Основные сведения
- •Подготовительный вариант
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 15. Линейная функция Основные сведения
- •Если угловые коэффициенты прямых, являющихся графиками линейных функций, различны, то прямые пересекаются, если угловые коэффициенты прямых равны, то прямые параллельны. Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 17. Линейные уравнения с двумя переменными Основные сведения Равенство, содержащее выражения с двумя переменными, называется уравнением с двумя переменными.
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 18. Системы линейных уравнений и способы их решения
- •Вариант 1
- •Вариант 2
- •Вариант 3
Подготовительный вариант
Среди пар чисел
 ,
, ,
, и
и найдите решение уравнения
найдите решение уравнения .
.В одной системе координат постройте графики уравнений
 ;
;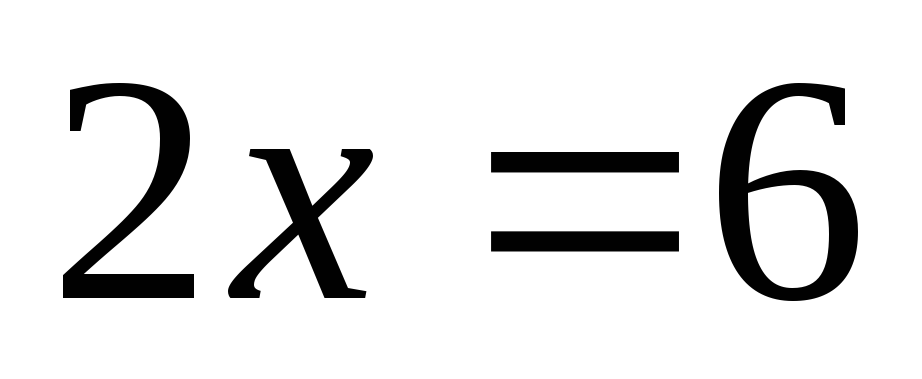 и
и .
Найдите по графику координаты точек
пересечения этих прямых.
.
Найдите по графику координаты точек
пересечения этих прямых.При каком значении
 пара чисел
пара чисел является решением уравнения
является решением уравнения ?
?Найдите точки пересечения с осями координат графика уравнения
 .
.Из уравнения
 выразите переменную
выразите переменную .
.При каком значении параметра
 график уравнения
график уравнения параллелен: а) оси абсцисс; б) оси ординат?
параллелен: а) оси абсцисс; б) оси ординат?Решите уравнение
 в целых числах. Укажите три различных
целочисленных решения этого уравнения.
в целых числах. Укажите три различных
целочисленных решения этого уравнения.Постройте график уравнения
 .
Сколько точек пересечения имеет график
данного уравнения с прямой, параллельной
оси ординат?
.
Сколько точек пересечения имеет график
данного уравнения с прямой, параллельной
оси ординат?
Вариант 1
Среди пар чисел
 ,
, и
и найдите решение уравнения
найдите решение уравнения .
.В одной системе координат постройте графики уравнений
 ;
; и
и .
Найдите по графику координаты точек
пересечения этих прямых.
.
Найдите по графику координаты точек
пересечения этих прямых.При каком значении
 пара чисел
пара чисел является решением уравнения
является решением уравнения ?
?Найдите точки пересечения с осями координат графика уравнения
 .
.Из уравнения
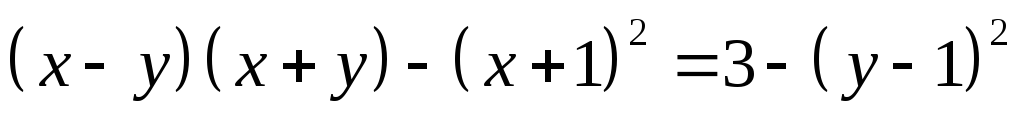 выразите переменную: а)
выразите переменную: а) ;
б)
;
б) .
.При каком значении параметра
 график уравнения
график уравнения параллелен: а) оси абсцисс; б) оси ординат?
параллелен: а) оси абсцисс; б) оси ординат?Решите уравнение
 в целых числах. Укажите три различных
целочисленных решения этого уравнения.
в целых числах. Укажите три различных
целочисленных решения этого уравнения.Постройте график уравнения
 .
Сколько точек пересечения имеет график
данного уравнения с прямой, параллельной
оси ординат, в зависимости от переменной
.
Сколько точек пересечения имеет график
данного уравнения с прямой, параллельной
оси ординат, в зависимости от переменной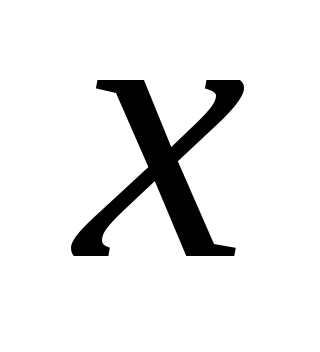 ?
?
Вариант 2
Среди пар чисел
 ,
,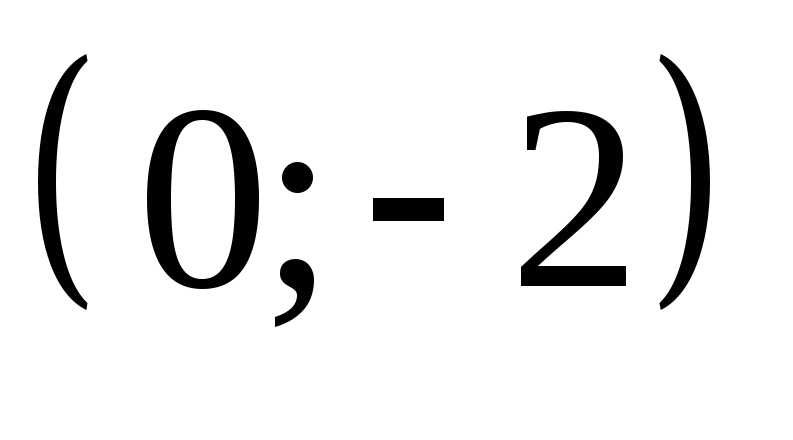 и
и найдите решение уравнения
найдите решение уравнения .
.В одной системе координат постройте графики уравнений
 ;
; и
и .
Найдите по графику координаты точек
пересечения этих прямых.
.
Найдите по графику координаты точек
пересечения этих прямых.При каком значении
 пара чисел
пара чисел является решением уравнения
является решением уравнения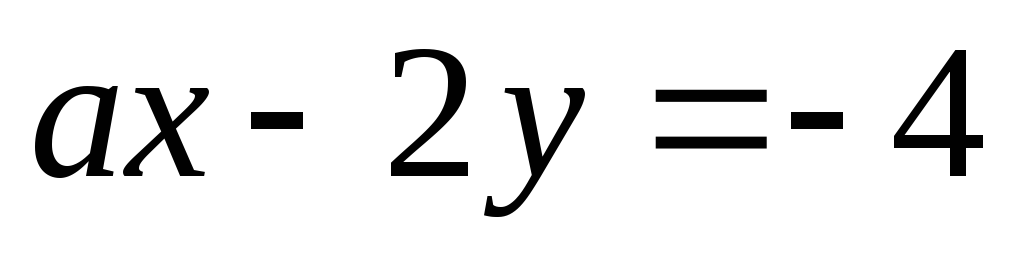 ?
?Найдите точки пересечения с осями координат графика уравнения
 .
.Из уравнения
 выразите переменную: а)
выразите переменную: а) ;
б)
;
б) .
.При каком значении параметра
 график уравнения
график уравнения параллелен: а) оси абсцисс; б) оси ординат?
параллелен: а) оси абсцисс; б) оси ординат?Решите уравнение
 в целых числах. Укажите три различных
целочисленных решения этого уравнения.
в целых числах. Укажите три различных
целочисленных решения этого уравнения.Постройте график уравнения
 .
Сколько точек пересечения имеет график
данного уравнения с прямой, параллельной
оси ординат, в зависимости от переменной
.
Сколько точек пересечения имеет график
данного уравнения с прямой, параллельной
оси ординат, в зависимости от переменной ?
?
Вариант 3
Среди упорядоченных пар чисел
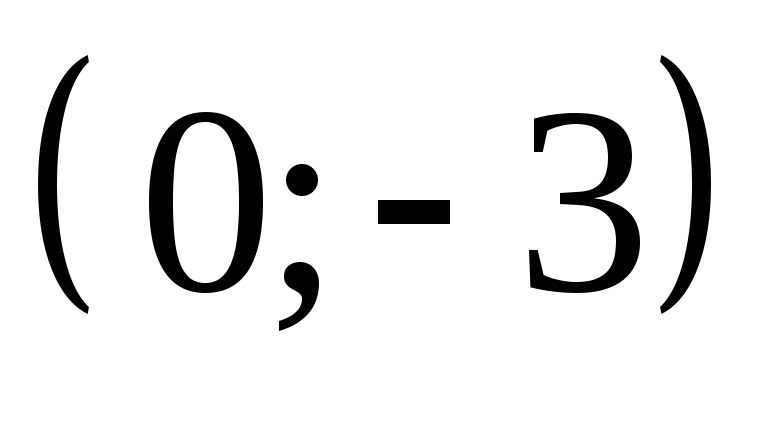 ,
, и
и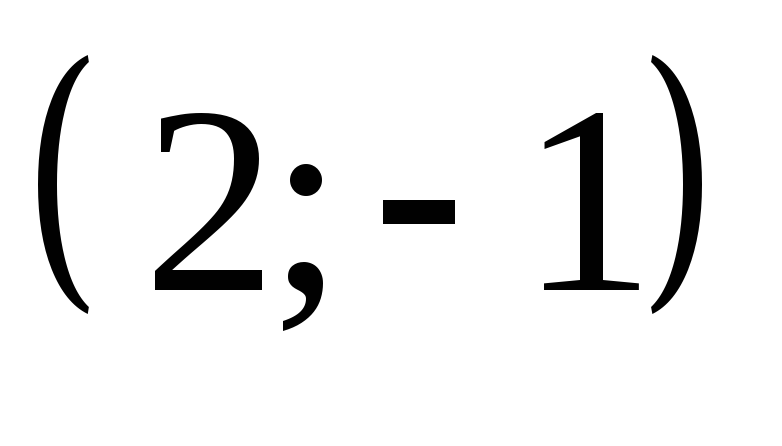 найдите решение уравнения
найдите решение уравнения .
.В одной системе координат постройте графики уравнений
 ;
; и
и .
Найдите по графику координаты точек
пересечения этих прямых.
.
Найдите по графику координаты точек
пересечения этих прямых.При каком значении параметра
 пара чисел
пара чисел является решением уравнения
является решением уравнения ?
?Найдите точки пересечения с осями координат графика уравнения
 .
.Из уравнения
 выразите переменную: а)
выразите переменную: а) ;
б)
;
б) .
.При каком значении параметра
 график уравнения
график уравнения параллелен: а) оси абсцисс; б) оси ординат?
параллелен: а) оси абсцисс; б) оси ординат?Решите уравнение
 в целых числах. Укажите три различные
целочисленные решения этого уравнения.
в целых числах. Укажите три различные
целочисленные решения этого уравнения.Постройте график уравнения
 .
Сколько точек пересечения имеет график
данного уравнения с прямой, параллельной
оси абсцисс?
.
Сколько точек пересечения имеет график
данного уравнения с прямой, параллельной
оси абсцисс?
Самостоятельная работа № 24
§ 18. Системы линейных уравнений и способы их решения
Основные сведения
Если требуется найти все общие решения двух уравнений, то говорят, что нужно решить систему уравнений.
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное числовое равенство.
Основные способы решения систем уравнений с двумя переменными: графический способ, способ подстановки и способ сложения.
Подготовительный вариант
Является ли пара чисел
 решением системы: а)
решением системы: а) ;
б)
;
б) ?
?Решите систему уравнений методом подстановки: а)
 ;
б)
;
б) .
.Решите систему графическим способом
 .
.Найдите значение выражения
 ,
если
,
если и
и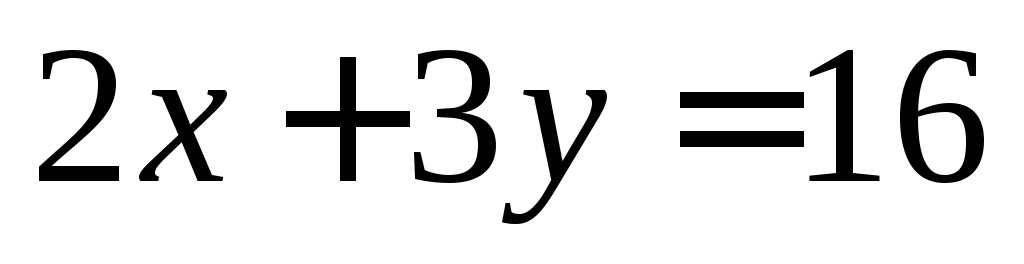 .
.При каких значениях параметров
 и
и решением системы
решением системы является пара чисел
является пара чисел ?
?Найдите, при каком отрицательном значении параметра
 система
система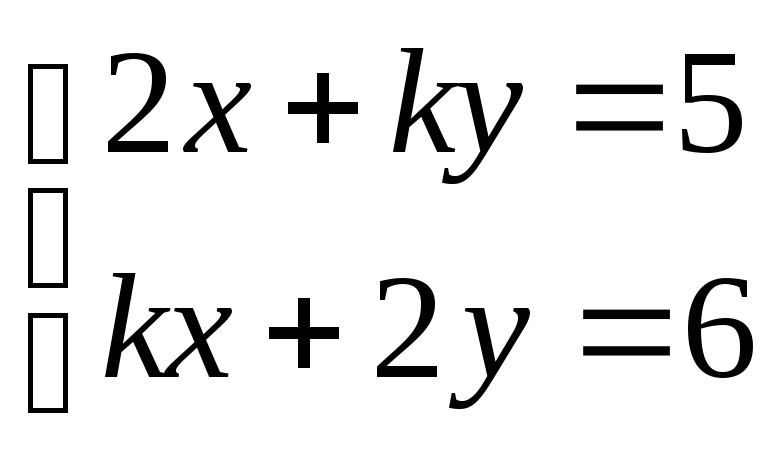 не имеет решений.
не имеет решений.Решите уравнение
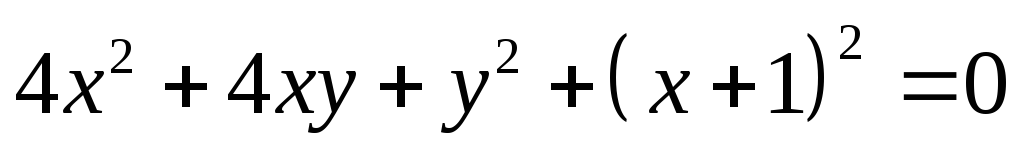 .
.
Вариант 1
Является ли пара чисел
 решением системы: а)
решением системы: а) ;
б)
;
б) ?
?Решите систему уравнений методом подстановки: а)
 ;
б)
;
б) .
.Решите систему графическим способом
 .
.Найдите значение выражения
 ,
если
,
если и
и .
.При каких значениях параметров
 и
и решением системы
решением системы является пара чисел
является пара чисел ?
?Найдите все значения параметра
 ,
при которых система
,
при которых система не имеет решений.
не имеет решений.Решите уравнение
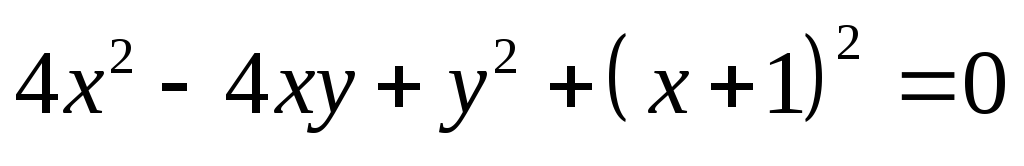 .
.
Вариант 2
Является ли пара чисел
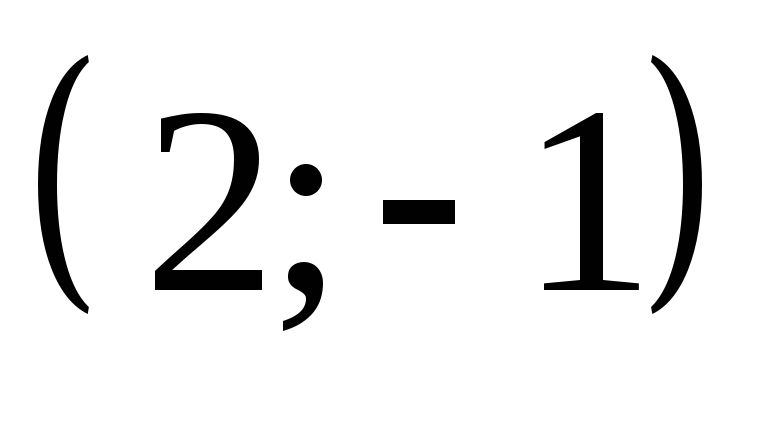 решением системы: а)
решением системы: а) ;
б)
;
б) ?
?Решите систему уравнений методом подстановки: а)
 ;
б)
;
б) .
.Решите систему графическим способом
 .
.Найдите значение выражения
 ,
если
,
если и
и .
.При каких значениях параметров
 и
и решением системы
решением системы является пара чисел
является пара чисел ?
?Найдите все значения параметра
 ,
при которых система
,
при которых система не имеет решений.
не имеет решений.Решите уравнение
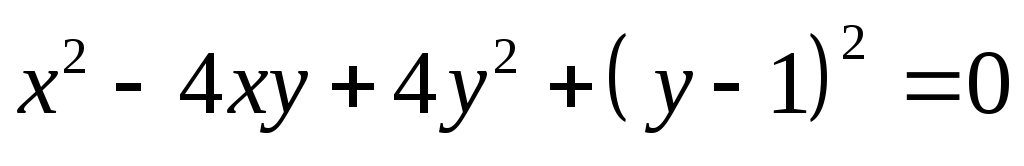 .
.
Вариант 3
Является ли пара чисел
 решением системы: а)
решением системы: а) ;
б)
;
б) ?
?Решите систему уравнений методом подстановки: а)
 ;
б)
;
б) .
.Решите систему графическим способом
 .
.Найдите значение выражения
 ,
если
,
если и
и .
.При каких значениях параметров
 и
и решением системы
решением системы является пара чисел
является пара чисел ?
?Найдите, при каком положительном значении параметра
 система
система не имеет решений.
не имеет решений.Решите уравнение
 .
.
Самостоятельная работа № 25
§ 18. Системы линейных уравнений и способы их решения
Основные сведения
При решении задач с помощью системы уравнений с несколькими переменными поступают следующим образом:
обозначают неизвестные числа буквами;
составляют систему уравнений, используя условие задачи;
решают эту систему;
истолковывают результат в соответствии с условием задачи.
При решении задач с помощью системы уравнений с несколькими переменными, как правило, составляют столько уравнений, сколько введено неизвестных.
Подготовительный вариант
Решите систему уравнений методом сложения: а)
 ;
б)
;
б) ;
в)
;
в) .
.Решите задачу, составив систему уравнений. Скорость моторной лодки по течению реки равна 14,3 км/ч, а против течения реки равна 12,1 км/ч. Найдите скорость течения реки и собственную скорость лодки.
Задайте формулой линейную функцию, график которой проходит через точки
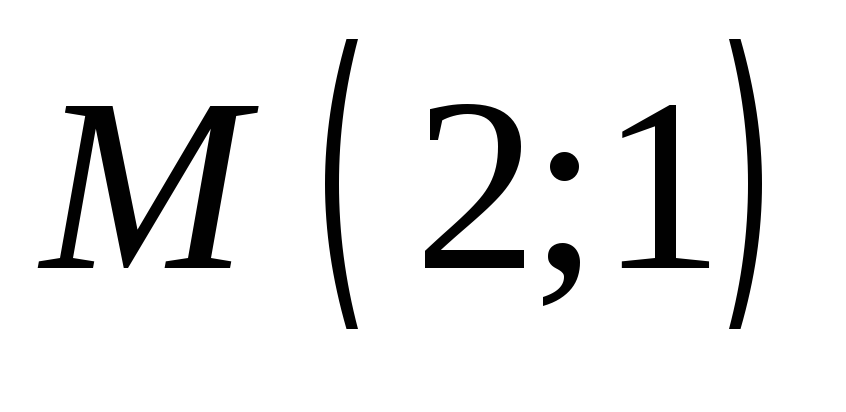 и
и .
.Масса туриста с рюкзаком в 5 раз больше массы одного рюкзака. Определите массы рюкзака и туриста в отдельности, если сумма масс двух рюкзаков и массы туриста равна 120 кг.
Разность квадратов двух натуральных чисел равна 21, а сумма этих чисел равна 7. Найдите эти числа.
Решите систему
 .
.Решите уравнение
 .
.
