
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 1. Множества Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 2. Числовые выражения и выражения с переменными Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 3. Степень с натуральным показателем Основные сведения
- •Подготовительный вариант
- •Подготовительный вариант
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 6. Сумма, разность и произведение многочленов Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 6. Сумма, разность и произведение многочленов Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 7. Уравнение с одной переменной Основные сведения Равенство, содержащее переменную, называется уравнением с одной переменой или уравнением с одним неизвестным.
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 8. Решение уравнений и задач Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 9. Способы разложения многочленов на множители
- •Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 10. Применение разложения многочлена на множители
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 12. Квадрат суммы и квадрат разности
- •§ 13. Куб суммы и куб разности, сумма и разность кубов Основные сведения
- •Подготовительный вариант
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 15. Линейная функция Основные сведения
- •Если угловые коэффициенты прямых, являющихся графиками линейных функций, различны, то прямые пересекаются, если угловые коэффициенты прямых равны, то прямые параллельны. Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 17. Линейные уравнения с двумя переменными Основные сведения Равенство, содержащее выражения с двумя переменными, называется уравнением с двумя переменными.
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 18. Системы линейных уравнений и способы их решения
- •Вариант 1
- •Вариант 2
- •Вариант 3
Вариант 1
В одной системе координат (единичный отрезок – один сантиметр) постройте графики функций
 ,
, и найдите абсциссы их точек пересечения.
и найдите абсциссы их точек пересечения.По графику функции
 (задание № 1) найдите значение аргумента,
при котором значение функции равно 8.
(задание № 1) найдите значение аргумента,
при котором значение функции равно 8.В одной системе координат (единичный отрезок – один сантиметр) постройте графики функций
 ,
, и найдите абсциссы их точек пересечения.
и найдите абсциссы их точек пересечения.По графику функции
 (задание № 3) найдите значение аргумента,
при котором значение функции равно 6.
(задание № 3) найдите значение аргумента,
при котором значение функции равно 6.Не вычисляя значений выражений, сравните: а)
 и
и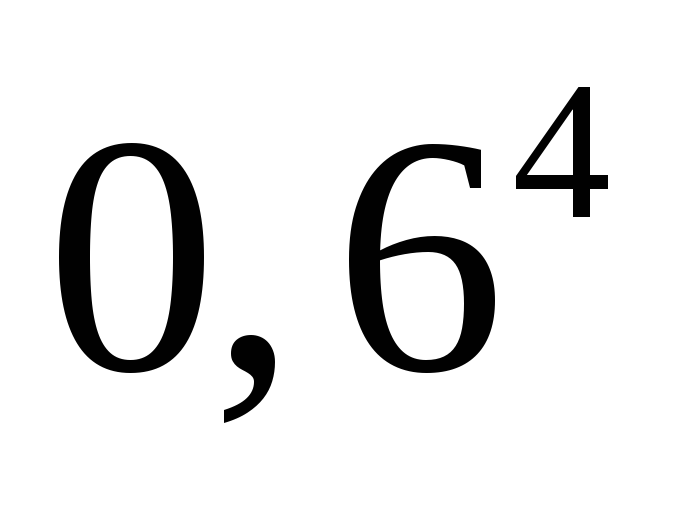 ;
б)
;
б) и
и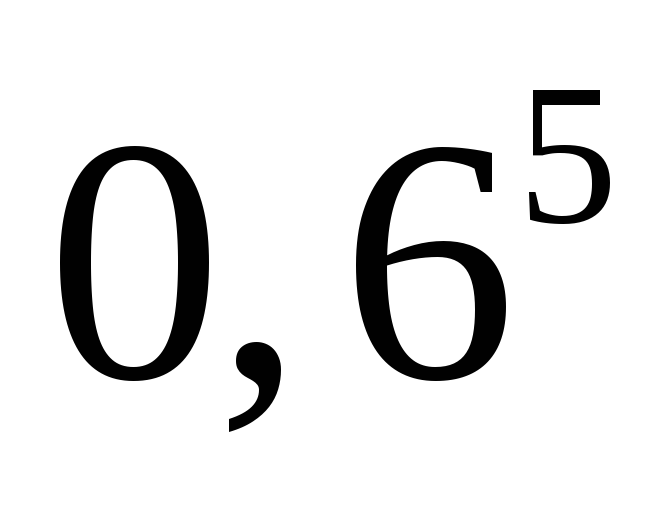 ;
в)
;
в) и
и ;
г)
;
г) и
и .
.Расположите числа
 ,
, и
и в порядке возрастания, если: а)
в порядке возрастания, если: а) ;
б)
;
б)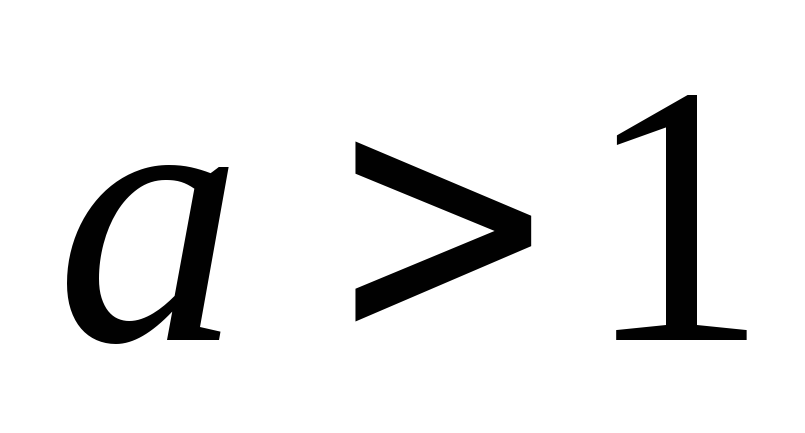 ;
в)
;
в) ;
г)
;
г) .
.Задайте формулой линейную функцию, график которой проходит через точку
 и не имеет с графиком функции
и не имеет с графиком функции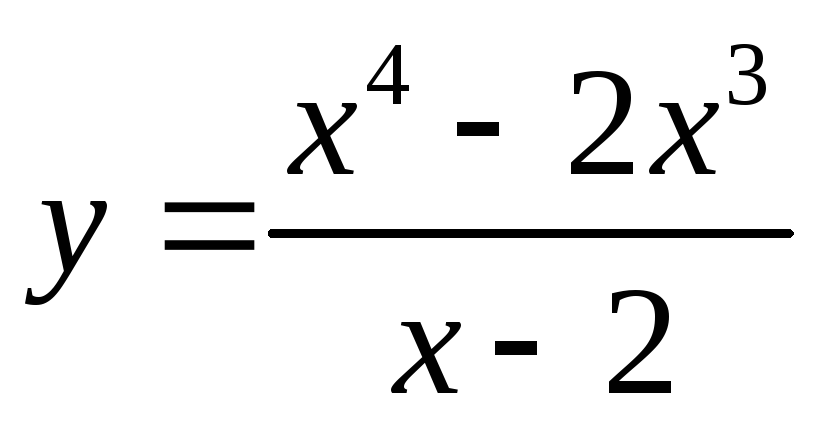 общих точек.
общих точек.
Вариант 2
В одной системе координат (единичный отрезок – один сантиметр) постройте графики функций
 ,
, и найдите абсциссы их точек пересечения.
и найдите абсциссы их точек пересечения.По графику функции
 (задание № 1) найдите значение аргумента,
при котором значение функции равно 6.
(задание № 1) найдите значение аргумента,
при котором значение функции равно 6.В одной системе координат (единичный отрезок – один сантиметр) постройте графики функций
 ,
, и найдите абсциссы их точек пересечения.
и найдите абсциссы их точек пересечения.По графику функции
 (задание № 3) найдите значение аргумента,
при котором значение функции равно 4.
(задание № 3) найдите значение аргумента,
при котором значение функции равно 4.Не вычисляя значений выражений, сравните: а)
 и
и ;
б)
;
б) и
и ;
в)
;
в) и
и ;
г)
;
г) и
и .
.Расположите числа
 ,
, и
и в порядке возрастания, если: а)
в порядке возрастания, если: а) ;
б)
;
б) ;
в)
;
в) ;
г)
;
г) .
.Задайте формулой линейную функцию, график которой проходит через точку
 и не имеет с графиком функции
и не имеет с графиком функции общих точек.
общих точек.
Вариант 3
В одной системе координат (единичный отрезок – один сантиметр) постройте графики функций
 ,
, ;
если графики имеют общие точки, то
найдите абсциссы этих точек.
;
если графики имеют общие точки, то
найдите абсциссы этих точек.По графику функции
 (задание № 1) найдите значение аргумента,
при котором значение функции равно 3.
(задание № 1) найдите значение аргумента,
при котором значение функции равно 3.В одной системе координат (единичный отрезок – один сантиметр) постройте графики функций
 ,
, ;
если графики имеют общие точки, то
найдите ординаты этих точек.
;
если графики имеют общие точки, то
найдите ординаты этих точек.По графику функции
 (задание № 3) найдите значение аргумента,
при котором значение функции равно 3.
(задание № 3) найдите значение аргумента,
при котором значение функции равно 3.Не вычисляя значений выражений, сравните: а)
 и
и ;
б)
;
б) и
и ;
в)
;
в)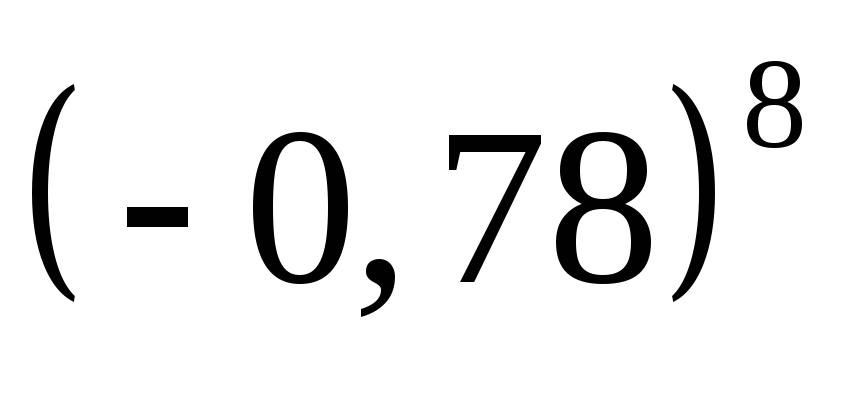 и
и ;
г)
;
г) и
и .
.Расположите числа
 ,
, и
и в порядке возрастания, если: а)
в порядке возрастания, если: а) ;
б)
;
б) ;
в)
;
в) ;
г)
;
г) .
.Задайте формулой линейную функцию, график которой проходит через точку
 и не имеет с графиком функции
и не имеет с графиком функции общих точек.
общих точек.
Самостоятельная работа № 23
§ 17. Линейные уравнения с двумя переменными Основные сведения Равенство, содержащее выражения с двумя переменными, называется уравнением с двумя переменными.
Решением уравнения с двумя переменными называется упорядоченная пара чисел, обращающая это уравнение в верное числовое равенство.
Уравнения с двумя переменными, имеющие одно и то же множество решений, называются равносильными.
Свойства уравнений с двумя переменными такие же, как и свойства уравнений с одной переменной.
Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых являются решениями этого уравнения.
Линейным уравнением
с двумя переменными
называется уравнение вида
![]() ,
где
,
где![]() и
и![]() – переменные,
– переменные,![]() ,
,![]() и
и![]() – некоторые числа.
– некоторые числа.
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.
Если в линейном уравнении коэффициенты при переменных равны нулю, а свободный член не равен нулю, то его график – пустое множество.
Если коэффициенты при переменных и свободный член линейного уравнения равны нулю, то его графиком является вся координатная плоскость.
Если в задании требуется найти все целочисленные решения уравнения с двумя переменными, то говорят о решении уравнения в целых числах.
