
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 1. Множества Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 2. Числовые выражения и выражения с переменными Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 3. Степень с натуральным показателем Основные сведения
- •Подготовительный вариант
- •Подготовительный вариант
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 6. Сумма, разность и произведение многочленов Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 6. Сумма, разность и произведение многочленов Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 7. Уравнение с одной переменной Основные сведения Равенство, содержащее переменную, называется уравнением с одной переменой или уравнением с одним неизвестным.
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 8. Решение уравнений и задач Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 9. Способы разложения многочленов на множители
- •Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 10. Применение разложения многочлена на множители
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 12. Квадрат суммы и квадрат разности
- •§ 13. Куб суммы и куб разности, сумма и разность кубов Основные сведения
- •Подготовительный вариант
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 15. Линейная функция Основные сведения
- •Если угловые коэффициенты прямых, являющихся графиками линейных функций, различны, то прямые пересекаются, если угловые коэффициенты прямых равны, то прямые параллельны. Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 17. Линейные уравнения с двумя переменными Основные сведения Равенство, содержащее выражения с двумя переменными, называется уравнением с двумя переменными.
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 18. Системы линейных уравнений и способы их решения
- •Вариант 1
- •Вариант 2
- •Вариант 3
§ 15. Линейная функция Основные сведения
Функция, которую
можно задать формулой вида
![]() ,
где
,
где![]() – независимая переменная,
– независимая переменная,![]() и
и![]() – произвольные числа, называетсялинейной
функцией.
– произвольные числа, называетсялинейной
функцией.
Коэффициент
![]() ,
стоящий перед аргументом
,
стоящий перед аргументом![]() в формуле линейной функции, называетсяугловым
коэффициентом прямой,
являющейся графиком данной линейной
функции. Геометрический смысл углового
коэффициента прямой будет рассмотрен
позже. Коэффициент
в формуле линейной функции, называетсяугловым
коэффициентом прямой,
являющейся графиком данной линейной
функции. Геометрический смысл углового
коэффициента прямой будет рассмотрен
позже. Коэффициент
![]() показывает, на сколько единичных отрезков
вверх или вниз смещен график прямой
пропорциональности
показывает, на сколько единичных отрезков
вверх или вниз смещен график прямой
пропорциональности![]() ,
т.е. указывает точку пересечения графика
линейной функции с осью ординат:
,
т.е. указывает точку пересечения графика
линейной функции с осью ординат:![]() .
.
Если угловые коэффициенты прямых, являющихся графиками линейных функций, различны, то прямые пересекаются, если угловые коэффициенты прямых равны, то прямые параллельны. Подготовительный вариант
Найдите координаты вершин треугольника, стороны которого лежат на прямых
 ,
, и
и .
.При каких значениях параметра
 прямая
прямая проходит: а) хотя бы через одну точку
графика функции
проходит: а) хотя бы через одну точку
графика функции ;
б) хотя бы через одну точку отрезка с
вершинами в точках
;
б) хотя бы через одну точку отрезка с
вершинами в точках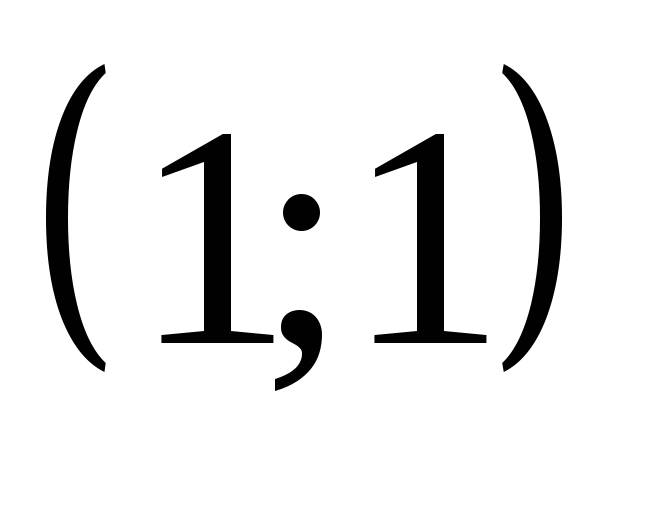 и
и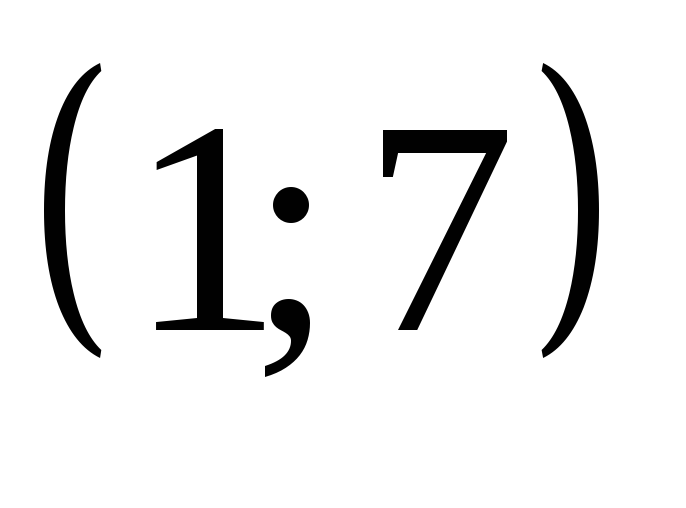 ?
?При каких значениях параметра
 график функции
график функции проходит хотя бы через одну точку,
абсцисса которой положительна, а
ордината – отрицательна?
проходит хотя бы через одну точку,
абсцисса которой положительна, а
ордината – отрицательна?Найдите координаты точки графика функции
 ,
сумма абсциссы и ординаты которой равна
19.
,
сумма абсциссы и ординаты которой равна
19.На координатной плоскости задано множество точек
 таких, ординаты которых вычисляются
по формуле
таких, ординаты которых вычисляются
по формуле .
Изобразите на координатной плоскости
три точки, принадлежащие этому множеству.
Чему равна абсцисса точки
.
Изобразите на координатной плоскости
три точки, принадлежащие этому множеству.
Чему равна абсцисса точки ,
если известно, что точка
,
если известно, что точка – одна из точек этого множества?
– одна из точек этого множества?При каких значениях
 и
и графики функций
графики функций и
и симметричны относительно оси: а) абсцисс;
б) ординат? Ответ проиллюстрируйте на
рисунках.
симметричны относительно оси: а) абсцисс;
б) ординат? Ответ проиллюстрируйте на
рисунках.
Вариант 1
Найдите координаты вершин треугольника, ограниченного прямыми
 ,
, и
и .
.При каких значениях параметра
 график прямой пропорциональности
график прямой пропорциональности проходит: а) хотя бы через одну точку
графика функции
проходит: а) хотя бы через одну точку
графика функции ;
б) только через одну точку отрезка
;
б) только через одну точку отрезка ,
где
,
где ,
, .
.При каких значениях параметра
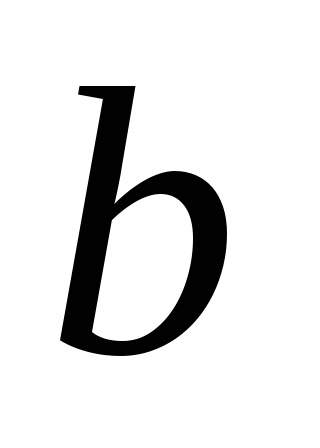 график функции
график функции проходит хотя бы через одну точку,
абсцисса которой отрицательна, а
ордината – положительна?
проходит хотя бы через одну точку,
абсцисса которой отрицательна, а
ордината – положительна?Найдите координаты такой точки графика функции
 ,
сумма абсциссы и ординаты которой равна
4.
,
сумма абсциссы и ординаты которой равна
4.На координатной плоскости
 задано множество точек
задано множество точек таких, координаты которых связаны
соотношением
таких, координаты которых связаны
соотношением .
Изобразите это множество. Чему может
быть равна абсцисса точки
.
Изобразите это множество. Чему может
быть равна абсцисса точки ,
если известно, что эта точка не принадлежит
данному множеству?
,
если известно, что эта точка не принадлежит
данному множеству?При каких значениях
 и
и графики функций
графики функций и
и симметричны относительно оси: а) абсцисс;
б) ординат? Ответ проиллюстрируйте на
рисунках.
симметричны относительно оси: а) абсцисс;
б) ординат? Ответ проиллюстрируйте на
рисунках.
Вариант 2
Найдите координаты вершин треугольника, ограниченного прямыми
 ,
, и
и .
.При каких значениях параметра
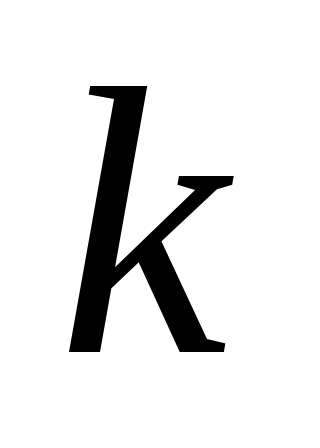 график прямой пропорциональности
график прямой пропорциональности проходит: а) хотя бы через одну точку
графика функции
проходит: а) хотя бы через одну точку
графика функции ;
б) только через одну точку отрезка
;
б) только через одну точку отрезка ,
где
,
где ,
, .
.При каких значениях параметра
 график функции
график функции проходит хотя бы через одну точку,
абсцисса которой положительна, а
ордината – отрицательна?
проходит хотя бы через одну точку,
абсцисса которой положительна, а
ордината – отрицательна?Найдите координаты такой точки графика функции
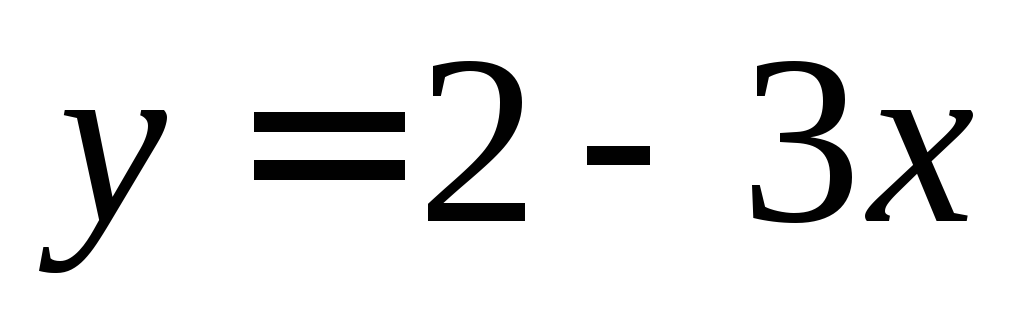 ,
сумма абсциссы и ординаты которой равна
4.
,
сумма абсциссы и ординаты которой равна
4.На координатной плоскости
 задано множество точек
задано множество точек таких, координаты которых связаны
соотношением
таких, координаты которых связаны
соотношением .
Изобразите это множество. Чему может
быть равна абсцисса точки
.
Изобразите это множество. Чему может
быть равна абсцисса точки ,
если известно, что эта точка не принадлежит
данному множеству?
,
если известно, что эта точка не принадлежит
данному множеству?При каких значениях
 и
и графики функций
графики функций и
и симметричны относительно оси: а) абсцисс;
б) ординат? Ответ проиллюстрируйте на
рисунках.
симметричны относительно оси: а) абсцисс;
б) ординат? Ответ проиллюстрируйте на
рисунках.
