
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 1. Множества Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 2. Числовые выражения и выражения с переменными Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 3. Степень с натуральным показателем Основные сведения
- •Подготовительный вариант
- •Подготовительный вариант
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 6. Сумма, разность и произведение многочленов Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 6. Сумма, разность и произведение многочленов Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 7. Уравнение с одной переменной Основные сведения Равенство, содержащее переменную, называется уравнением с одной переменой или уравнением с одним неизвестным.
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 8. Решение уравнений и задач Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 9. Способы разложения многочленов на множители
- •Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 10. Применение разложения многочлена на множители
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 12. Квадрат суммы и квадрат разности
- •§ 13. Куб суммы и куб разности, сумма и разность кубов Основные сведения
- •Подготовительный вариант
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 15. Линейная функция Основные сведения
- •Если угловые коэффициенты прямых, являющихся графиками линейных функций, различны, то прямые пересекаются, если угловые коэффициенты прямых равны, то прямые параллельны. Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 17. Линейные уравнения с двумя переменными Основные сведения Равенство, содержащее выражения с двумя переменными, называется уравнением с двумя переменными.
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 18. Системы линейных уравнений и способы их решения
- •Вариант 1
- •Вариант 2
- •Вариант 3
Подготовительный вариант
Найдите область определения функции: а)
 ;
б)
;
б) ;
в)
;
в) .
.
Рисунок 1
Дана функция .
Найдите: а) значение функции для значений
аргумента
.
Найдите: а) значение функции для значений
аргумента ;
б) значение аргумента, при котором
значение функции равно 4.
;
б) значение аргумента, при котором
значение функции равно 4.Функция
 задана графически (рисунок 1). Найдите:
а) значение функции при значении
аргумента, равном 2; б) значение аргумента,
при котором значение функции равно
нулю.
задана графически (рисунок 1). Найдите:
а) значение функции при значении
аргумента, равном 2; б) значение аргумента,
при котором значение функции равно
нулю.Функция задана формулой
 ,
где
,
где .
а) Задайте эту функцию таблицей с шагом
1. б) Задайте эту функцию графически. в)
Укажите наибольшее и наименьшее значения
функции и ее область значений.
.
а) Задайте эту функцию таблицей с шагом
1. б) Задайте эту функцию графически. в)
Укажите наибольшее и наименьшее значения
функции и ее область значений.Постройте график функции
 .
Укажите область определения и область
значений функции.
.
Укажите область определения и область
значений функции.Найдите область определения функции
 ,
где
,
где и постройте ее график.
и постройте ее график.
Вариант 1
Укажите область определения функции: а)
 ;
б)
;
б)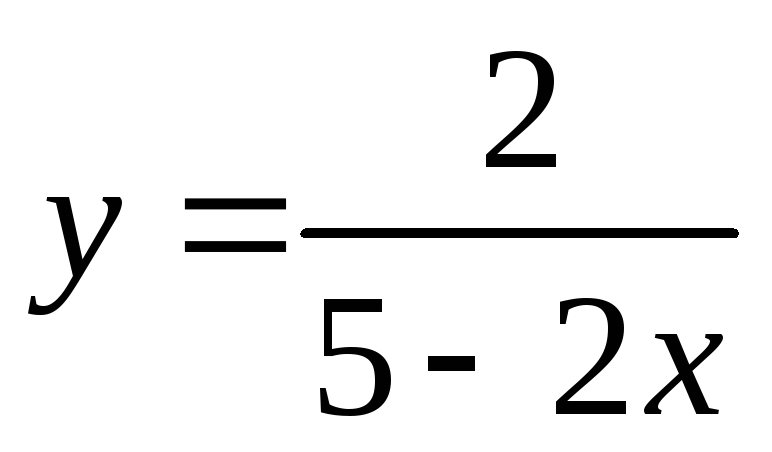 ;
в)
;
в) .
.
Рисунок 2
Дана функция .
Найдите: а) значение функции для значений
аргумента
.
Найдите: а) значение функции для значений
аргумента ;
б) значение аргумента, при котором
значение функции равно
;
б) значение аргумента, при котором
значение функции равно .
.Функция
 задана графически (рисунок 2). Найдите:
а) значение функции при значении
аргумента, равном 4; б) значение аргумента,
при котором значение функции равно 3.
задана графически (рисунок 2). Найдите:
а) значение функции при значении
аргумента, равном 4; б) значение аргумента,
при котором значение функции равно 3.Функция задана формулой
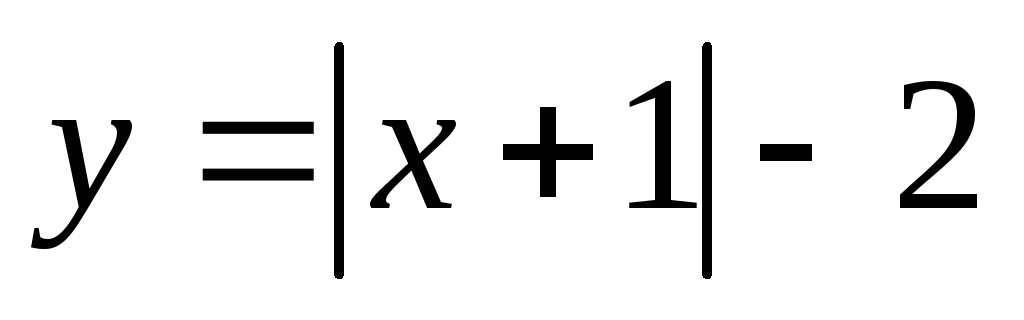 ,
где
,
где .
а) Задайте эту функцию таблицей с шагом
1. б) Задайте эту функцию графически. в)
Укажите наибольшее и наименьшее значения
функции и ее область значений.
.
а) Задайте эту функцию таблицей с шагом
1. б) Задайте эту функцию графически. в)
Укажите наибольшее и наименьшее значения
функции и ее область значений.Постройте график функции
 .
Какие из точек
.
Какие из точек ,
, ,
, принадлежат графику данной функции?
принадлежат графику данной функции?Найдите область определения функции
 ,
где
,
где ,
и постройте ее график.
,
и постройте ее график.
Вариант 2
Найдите область определения функции: а)
 ;
б)
;
б) ;
в)
;
в) .
.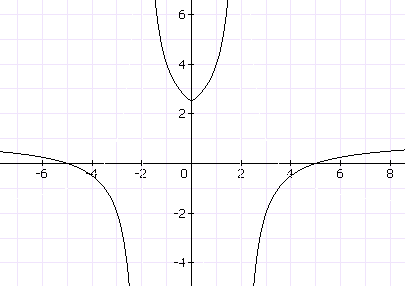
Рисунок 3
Дана функция .
Найдите: а) значение функции для значений
аргумента
.
Найдите: а) значение функции для значений
аргумента ;
б) значение аргумента, при котором
значение функции равно
;
б) значение аргумента, при котором
значение функции равно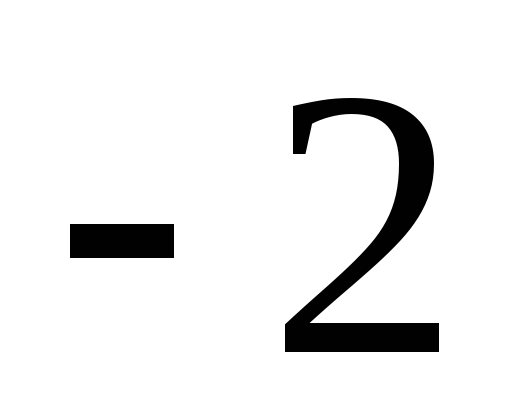 .
.Функция
 задана графически (рисунок 3). Найдите:
а) значение функции при значении
аргумента, равном
задана графически (рисунок 3). Найдите:
а) значение функции при значении
аргумента, равном ;
б) значение аргумента, при котором
значение функции равно 4.
;
б) значение аргумента, при котором
значение функции равно 4.Функция задана формулой
 ,
где
,
где .
а) Задайте эту функцию таблицей с шагом
1. б) Задайте эту функцию графически. в)
Укажите наибольшее и наименьшее значения
функции и ее область значений.
.
а) Задайте эту функцию таблицей с шагом
1. б) Задайте эту функцию графически. в)
Укажите наибольшее и наименьшее значения
функции и ее область значений.Постройте график функции
 .
Какие из точек
.
Какие из точек ,
, ,
, принадлежат графику данной функции?
принадлежат графику данной функции?Найдите область определения функции
 ,
где
,
где ,
и постройте ее график.
,
и постройте ее график.
Вариант 3
Найдите область определения функции: а)
 ;
б)
;
б) ;
в)
;
в) .
.
Рисунок 4
Дана функция .
Найдите: а) значение функции для значений
аргумента, равных
.
Найдите: а) значение функции для значений
аргумента, равных и 2; б) значение аргумента, при котором
значение функции равно
и 2; б) значение аргумента, при котором
значение функции равно .
.Функция
 задана графически (рисунок 4). Найдите:
а) значение функции при значении
аргумента, равном
задана графически (рисунок 4). Найдите:
а) значение функции при значении
аргумента, равном ;
б) значение аргумента, при котором
значение функции равно 2.
;
б) значение аргумента, при котором
значение функции равно 2.Функция задана формулой
 ,
где
,
где .
а) Задайте эту функцию таблицей с шагом
0,5. б) Задайте функцию графически. в)
Укажите наибольшее и наименьшее значения
функции.
.
а) Задайте эту функцию таблицей с шагом
0,5. б) Задайте функцию графически. в)
Укажите наибольшее и наименьшее значения
функции.Постройте график функции
 .
Укажите область определения и область
значений функции.
.
Укажите область определения и область
значений функции.Найдите область определения функции
 ,
где
,
где и постройте ее график.
и постройте ее график.
Самостоятельная работа № 20
§ 15. Линейная функция
Основные сведения
Функция,
которую можно задать формулой вида
![]() ,
где
,
где![]() – независимая переменная,
– независимая переменная,![]() – отличное от нуля число, называетсяпрямой
пропорциональностью.
Число
– отличное от нуля число, называетсяпрямой
пропорциональностью.
Число
![]() в формуле
в формуле![]() называетсякоэффициентом
пропорциональности.
Областью определения и областью значений
прямой пропорциональности является
множество всех чисел.
называетсякоэффициентом
пропорциональности.
Областью определения и областью значений
прямой пропорциональности является
множество всех чисел.
Графиком прямой
пропорциональности является прямая,
проходящая через начало координат.
Если
![]() ,
то график проходит вI
и III
координатных четвертях, а если
,
то график проходит вI
и III
координатных четвертях, а если
![]() ,
то воII
и IV
координатных четвертях.
,
то воII
и IV
координатных четвертях.
Функция, которую
можно задать формулой вида
![]() ,
где
,
где![]() – независимая переменная,
– независимая переменная,![]() и
и![]() – произвольные числа, называетсялинейной
функцией.
Областью определения линейной функции
является множество всех чисел. Областью
значений линейной функции является
либо множество всех чисел (при
– произвольные числа, называетсялинейной
функцией.
Областью определения линейной функции
является множество всех чисел. Областью
значений линейной функции является
либо множество всех чисел (при
![]() ),
либо число
),
либо число![]() ,
если
,
если![]() .
.
График линейной
функции
![]() при
при![]() –прямая,
являющаяся графиком функции
–прямая,
являющаяся графиком функции
![]() и смещенная на
и смещенная на![]() единичных отрезков вверх, если
единичных отрезков вверх, если![]() ,
или вниз, если
,
или вниз, если![]() .
Графиком линейной функции
.
Графиком линейной функции![]() при
при![]() являетсяпрямая,
параллельная оси абсцисс, проходящая
через точку
являетсяпрямая,
параллельная оси абсцисс, проходящая
через точку
![]() .
.
