
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 1. Множества Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 2. Числовые выражения и выражения с переменными Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 3. Степень с натуральным показателем Основные сведения
- •Подготовительный вариант
- •Подготовительный вариант
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 6. Сумма, разность и произведение многочленов Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 6. Сумма, разность и произведение многочленов Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 7. Уравнение с одной переменной Основные сведения Равенство, содержащее переменную, называется уравнением с одной переменой или уравнением с одним неизвестным.
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 8. Решение уравнений и задач Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 9. Способы разложения многочленов на множители
- •Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 10. Применение разложения многочлена на множители
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 12. Квадрат суммы и квадрат разности
- •§ 13. Куб суммы и куб разности, сумма и разность кубов Основные сведения
- •Подготовительный вариант
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 15. Линейная функция Основные сведения
- •Если угловые коэффициенты прямых, являющихся графиками линейных функций, различны, то прямые пересекаются, если угловые коэффициенты прямых равны, то прямые параллельны. Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 17. Линейные уравнения с двумя переменными Основные сведения Равенство, содержащее выражения с двумя переменными, называется уравнением с двумя переменными.
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 18. Системы линейных уравнений и способы их решения
- •Вариант 1
- •Вариант 2
- •Вариант 3
Подготовительный вариант
Представьте в виде многочлена: а)
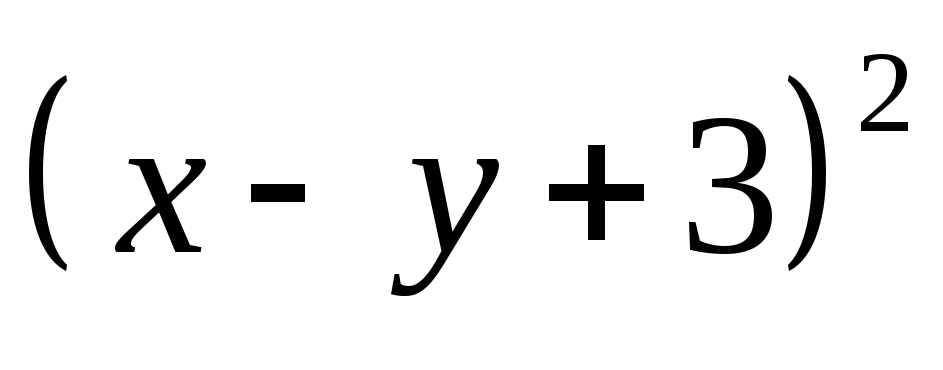 ;
б)
;
б) .
.Упростите выражение
 .
.Разложите на множители: а)
 ;
б)
;
б) .
.Найдите значение выражения
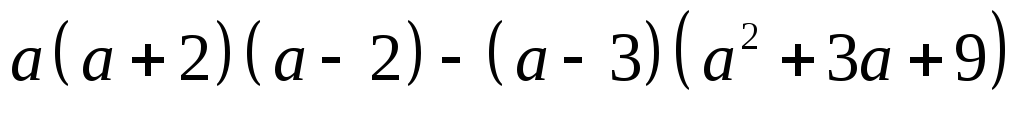 ,
где
,
где .
.Докажите, что
 кратно 13.
кратно 13.Найдите значение выражения
 .
.Решите уравнение: а)
 ;
б)
;
б) .
.Докажите, что выражение
 принимает лишь положительные значения
при любых значениях входящих в него
переменных.
принимает лишь положительные значения
при любых значениях входящих в него
переменных.
Вариант 1
Представьте в виде многочлена: а)
 ;
б)
;
б) .
.Упростите выражение
 .
.Разложите на множители: а)
 ;
б)
;
б) .
.Найдите значение выражения
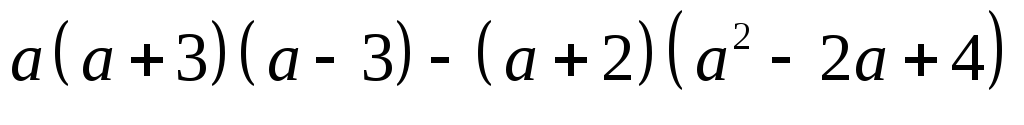 ,
где
,
где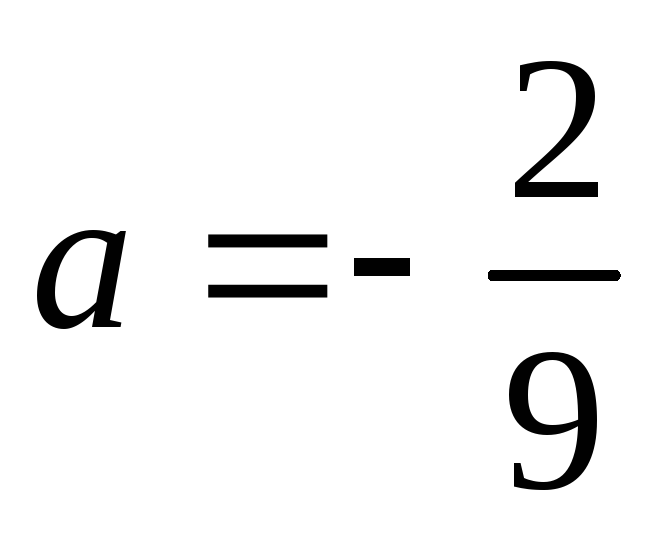 .
.Докажите, что
 кратно 9.
кратно 9.Найдите значение выражения
 .
.Найдите множество корней уравнения
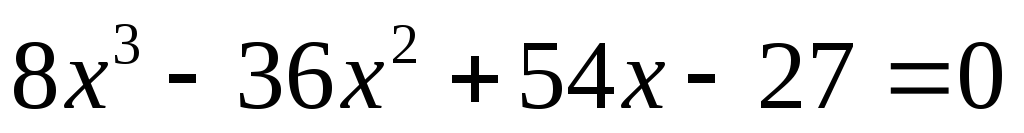 .
.Докажите, что выражение
 принимает лишь положительные значения
при любых значениях входящих в него
переменных.
принимает лишь положительные значения
при любых значениях входящих в него
переменных.
Вариант 2
Представьте в виде многочлена: а)
 ;
б)
;
б) .
.Упростите выражение
 .
.Разложите на множители: а)
 ;
б)
;
б) .
.Найдите значение выражения
 ,
где
,
где .
.Докажите, что
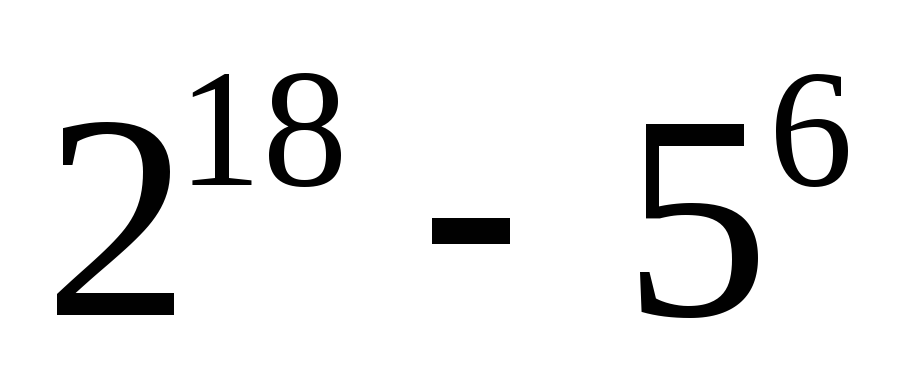 кратно 13.
кратно 13.Найдите значение выражения
 .
.Найдите множество корней уравнения
 .
.Докажите, что выражение
 принимает лишь положительные значения
при любых значениях входящих в него
переменных.
принимает лишь положительные значения
при любых значениях входящих в него
переменных.
Вариант 3
Представьте в виде многочлена: а)
 ;
б)
;
б) .
.Упростите выражение
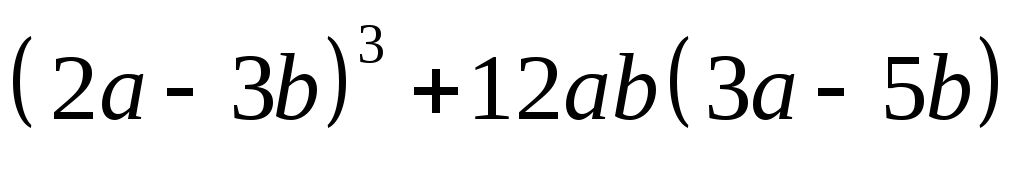 .
.Разложите на множители: а)
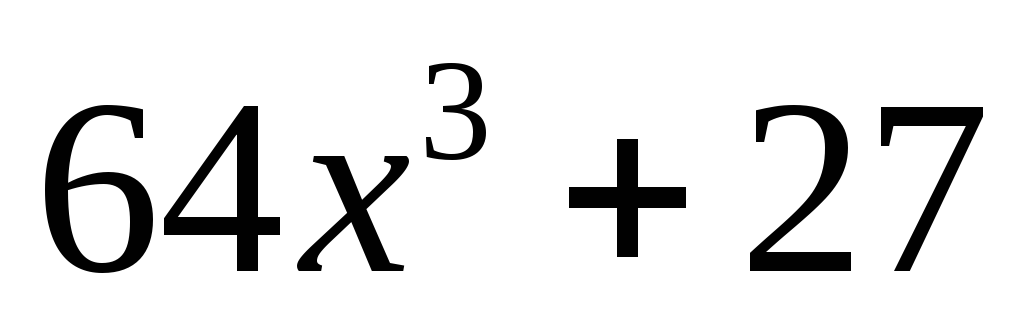 ;
б)
;
б) .
.Найдите значение выражения
 ,
где
,
где .
.Докажите, что
 кратно 7.
кратно 7.Найдите значение выражения
 .
.Найдите множество корней уравнения
 .
.Докажите, что выражение
 принимает лишь положительные значения
при любых значениях входящих в него
переменных.
принимает лишь положительные значения
при любых значениях входящих в него
переменных.
Самостоятельная работа № 18
§ 13. Куб суммы и куб разности, сумма и разность кубов
Основные сведения
![]() ,
,
![]() .
.
![]() для любых
для любых
![]() ,
,
![]() для нечетных
для нечетных
![]() .
.
Сумму
![]() для четных
для четных![]() в общем случае нельзя представить в
виде произведения.
в общем случае нельзя представить в
виде произведения.
Подготовительный вариант
Представьте в виде произведения выражение: а)
 ;
б)
;
б) ;
в)
;
в)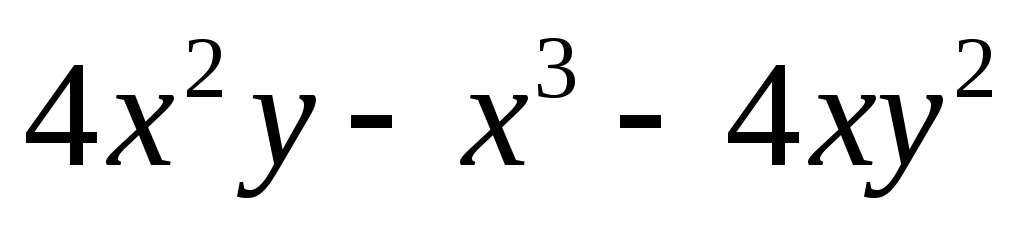 .
.Вычислите: а)
 ;
б)
;
б) ;
в)
;
в) .
.Разложите на множители выражение: а)
 ;
б)
;
б) ;
в)
;
в) .
.Решите уравнение
 .
.Найдите значение выражения
 .
.Докажите, что
 при любых
при любых кратно 5.
кратно 5.Представьте многочлен
 в виде произведения двух одинаковых
многочленов.
в виде произведения двух одинаковых
многочленов.Докажите, что значение выражения
 можно представить в виде произведения
двух одинаковых натуральных чисел.
можно представить в виде произведения
двух одинаковых натуральных чисел.
Вариант 1
Представьте в виде произведения выражение: а)
 ;
б)
;
б) ;
в)
;
в) .
.Вычислите: а)
 ;
б)
;
б) ;
в)
;
в) .
.Разложите на множители выражение: а)
 ;
б)
;
б) ;
в)
;
в) .
.Решите уравнение
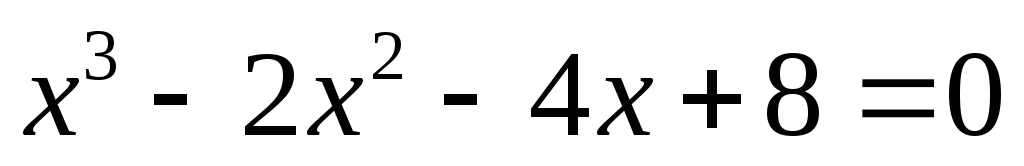 .
.Найдите значение выражения
 .
.Докажите, что
 при любых
при любых кратно 7.
кратно 7.Представьте многочлен
 в виде произведения.
в виде произведения.Докажите, что значение выражения
 можно представить в виде произведения
двух одинаковых натуральных чисел.
можно представить в виде произведения
двух одинаковых натуральных чисел.
Вариант 2
Представьте в виде произведения выражение: а)
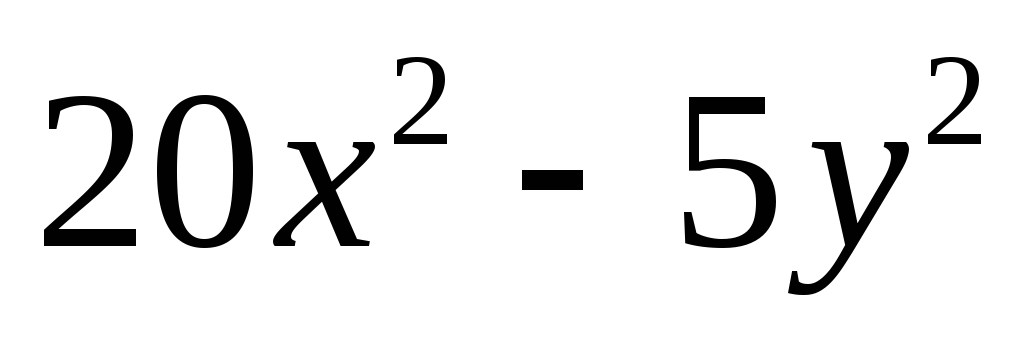 ;
б)
;
б)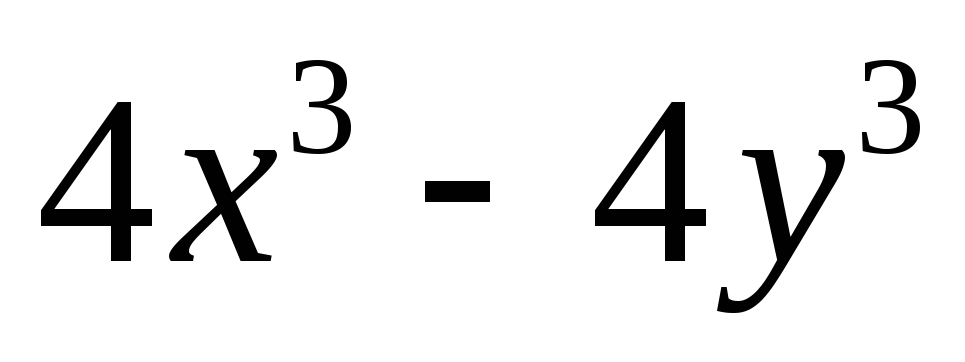 ;
в)
;
в) .
.Вычислите: а)
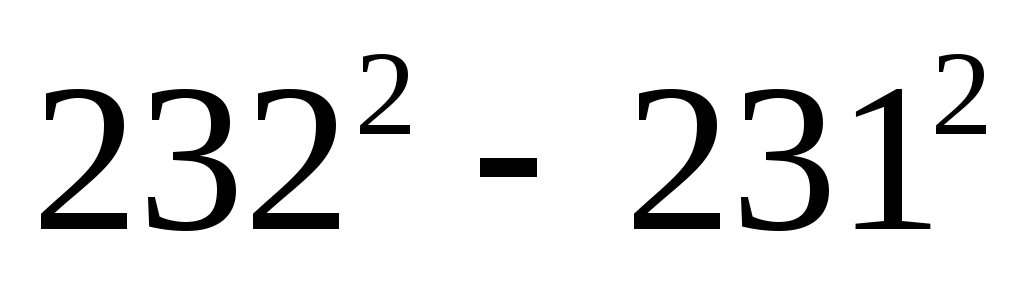 ;
б)
;
б) ;
в)
;
в) .
.Разложите на множители выражение: а)
 ;
б)
;
б) ;
в)
;
в) .
.Решите уравнение
 .
.Найдите значение выражения
 .
.Докажите, что
 при любых
при любых кратно 5.
кратно 5.Представьте многочлен
 в виде произведения.
в виде произведения.Докажите, что значение выражения
 можно представить в виде произведения
двух одинаковых натуральных чисел.
можно представить в виде произведения
двух одинаковых натуральных чисел.
Вариант 3
Представьте в виде произведения выражение: а)
 ;
б)
;
б) ;
в)
;
в) .
.Вычислите: а)
 ;
б)
;
б)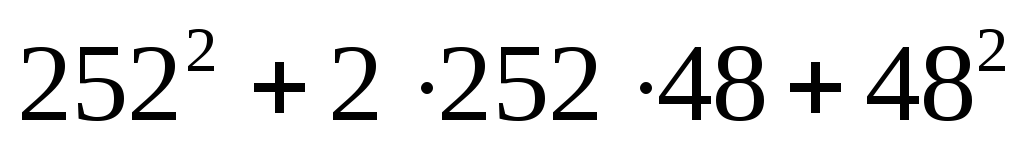 ;
в)
;
в) .
.Разложите на множители выражение: а)
 ;
б)
;
б) ;
в)
;
в) .
.Решите уравнение
 .
.Найдите значение выражения
 .
.Докажите, что
 при любых
при любых кратно 3.
кратно 3.Представьте многочлен
 в виде произведения.
в виде произведения.Докажите, что значение выражения
 можно представить в виде произведения
двух одинаковых натуральных чисел.
можно представить в виде произведения
двух одинаковых натуральных чисел.
Самостоятельная работа № 19
§ 14. Функции и их графики
Основные сведения
Функцией
называется соответствие между двумя
множествами, при котором каждому элементу
![]() множества
множества![]() соответствует единственный элемент
соответствует единственный элемент![]() множества
множества![]() .
Переменную
.
Переменную![]() называютнезависимой
переменной
или аргументом,
переменную
называютнезависимой
переменной
или аргументом,
переменную
![]() –зависимой
переменной
или функцией.
–зависимой
переменной
или функцией.
Функции можно задать аналитически (формулой), таблицей, описанием, графически. Если значения аргумента и значения функции – числа, то функция называется числовой.
Множество всех значений аргумента составляет область определения функции, множество всех значений функции – область значений функции. Если функция на различных частях области определения задается различными формулами, то говорят о кусочно-заданной функции.
Графиком функции
называется множество всех таких точек
координатной плоскости, абсциссы которых
равны значениям аргумента, а ординаты
– соответствующим значениям функции.
Если точка
![]() принадлежит графику функции
принадлежит графику функции![]() ,
то ее координаты удовлетворяют формуле
,
то ее координаты удовлетворяют формуле![]() ,
т.е. равенство
,
т.е. равенство![]() является верным. Наоборот, если пара
чисел
является верным. Наоборот, если пара
чисел![]() обращает формулу
обращает формулу![]() в верное числовое равенство, т.е.
в верное числовое равенство, т.е.![]() ,
то точка с координатами
,
то точка с координатами![]() принадлежит графику функции
принадлежит графику функции![]() .
.
