Вариант 1

1. Запишите в стандартном виде и укажите: а) старший коэффициент квадратного трехчлена ; б) свободный член квадратного трехчлена.

2. Выделите квадрат двучлена из квадратного трехчлена: а) ; б).

3. Разложите на множители квадратный трехчлен, выделив квадрат двучлена: а) ; б).

4. Решите уравнение , разложив его левую часть на множители с помощью выделения квадрата двучлена и применив формулу разности квадратов двух выражений.

5. Докажите, что при любых значениях переменной значение квадратного трехчлена: а) положительно; б)отрицательно.

6. Найдите: а) наименьшее значение квадратного трехчлена ; б) наибольшее значение квадратного трехчлена. Укажите, при каких значениях переменной достигаются экстремальные значения этих квадратных трехчленов.

7. Дан прямоугольник со сторонами 3 и 5 см. Большую его сторону уменьшили на см, а меньшую увеличили насм. При каком значенииплощадь полученного прямоугольника будет наибольшей?

Вариант 2

1. Запишите в стандартном виде и укажите: а) старший коэффициент квадратного трехчлена ; б) свободный член квадратного трехчлена.

2. Выделите квадрат двучлена из квадратного трехчлена: а) ; б).

3. Разложите на множители квадратный трехчлен, выделив квадрат двучлена: а) ; б).

4. Решите уравнение , разложив его левую часть на множители с помощью выделения квадрата двучлена и применив формулу разности квадратов двух выражений.

5. Докажите, что при любых значениях переменной значение квадратного трехчлена: а) положительно; б)отрицательно.

6. Найдите: а) наименьшее значение квадратного трехчлена ; б) наибольшее значение квадратного трехчлена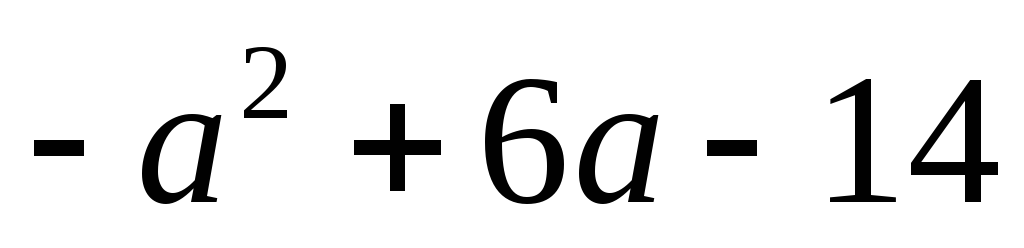. Укажите, при каких значениях переменной достигаются экстремальные значения этих квадратных трехчленов.

7. Дан прямоугольник со сторонами 8 и 12 см. Большую его сторону уменьшили на см, а меньшую увеличили насм. При каком значенииплощадь полученного прямоугольника будет наибольшей?

Вариант 3

1. Запишите в стандартном виде и укажите: а) старший коэффициент квадратного трехчлена ; б) свободный член квадратного трехчлена.

2. Выделите квадрат двучлена из квадратного трехчлена: а) ; б).

3. Разложите на множители квадратный трехчлен, выделив квадрат двучлена: а) ; б).

4. Решите уравнение 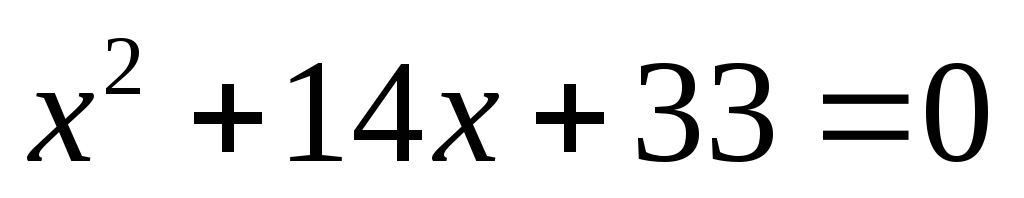, разложив его левую часть на множители с помощью выделения квадрата двучлена и применив формулу разности квадратов двух выражений.

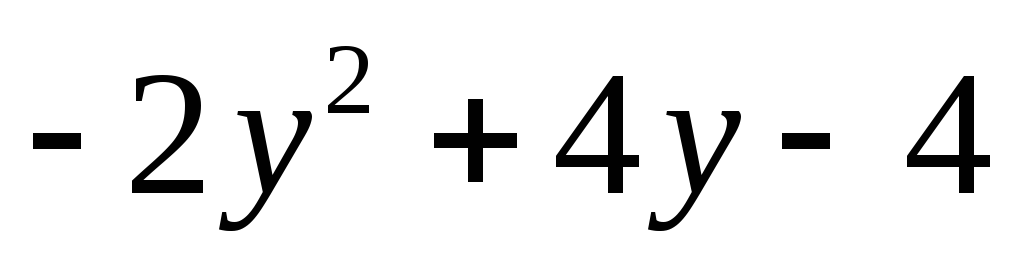5. Докажите, что при любых значениях переменной значение квадратного трехчлена: а) положительно; б)отрицательно.

6. Найдите: а) наименьшее значение квадратного трехчлена ; б) наибольшее значение квадратного трехчлена. Укажите, при каких значениях переменной достигаются экстремальные значения этих квадратных трехчленов.

7. Дан прямоугольник со сторонами 4 и 14 см. Большую его сторону уменьшили на см, а меньшую увеличили насм. При каком значенииплощадь полученного прямоугольника будет наибольшей?

Самостоятельная работа № 17

§ 12. Квадрат суммы и квадрат разности

§ 13. Куб суммы и куб разности, сумма и разность кубов Основные сведения

,

,

и, вообще, квадрат суммы нескольких выражений равен сумме квадратов этих выражений и всех удвоенных произведений этих выражений, взятых по два.

, т.е.

куб суммы двух выражений равен кубу первого выражения, плюс утроенное произведение квадрата первого выражения и второго, плюс утроенное произведение первого выражения и квадрата второго, плюс куб второго выражения.

, т.е.

куб разности двух выражений равен кубу первого выражения, минус утроенное произведение квадрата первого выражения и второго, плюс утроенное произведение первого выражения и квадрата второго, минус куб второго выражения.

, т.е.

сумма кубов двух выражений равна произведению суммы этих выражений и их неполного квадрата разности.

, т.е.

разность кубов двух выражений равна произведению разности этих выражений и их неполного квадрата суммы.