
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 1. Множества Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 2. Числовые выражения и выражения с переменными Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 3. Степень с натуральным показателем Основные сведения
- •Подготовительный вариант
- •Подготовительный вариант
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 6. Сумма, разность и произведение многочленов Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 6. Сумма, разность и произведение многочленов Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 7. Уравнение с одной переменной Основные сведения Равенство, содержащее переменную, называется уравнением с одной переменой или уравнением с одним неизвестным.
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 8. Решение уравнений и задач Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 9. Способы разложения многочленов на множители
- •Основные сведения
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 10. Применение разложения многочлена на множители
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 12. Квадрат суммы и квадрат разности
- •§ 13. Куб суммы и куб разности, сумма и разность кубов Основные сведения
- •Подготовительный вариант
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 15. Линейная функция Основные сведения
- •Если угловые коэффициенты прямых, являющихся графиками линейных функций, различны, то прямые пересекаются, если угловые коэффициенты прямых равны, то прямые параллельны. Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 17. Линейные уравнения с двумя переменными Основные сведения Равенство, содержащее выражения с двумя переменными, называется уравнением с двумя переменными.
- •Подготовительный вариант
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •§ 18. Системы линейных уравнений и способы их решения
- •Вариант 1
- •Вариант 2
- •Вариант 3
Вариант 1
Вынесите за скобку общий множитель: а)
 ;
б)
;
б) ;
в)
;
в)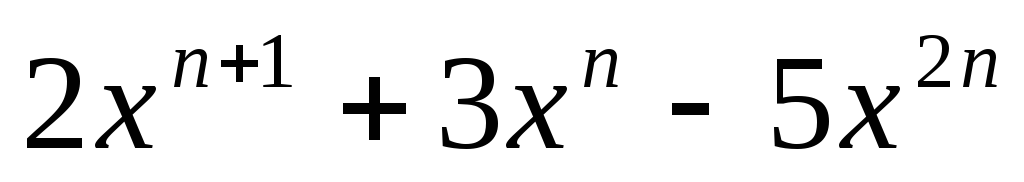 ,
где
,
где ,
, .
.Разложите на множители выражение: а)
 ;
б)
;
б) ;
в)
;
в) ,
где
,
где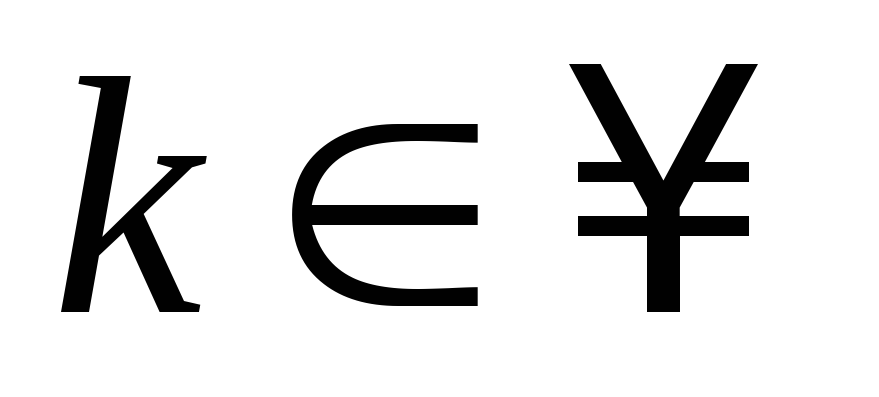 .
.Найдите значение выражения
 при
при ,
, .
.Известно, что при некотором значении переменной
 значение выражения
значение выражения равно 9. Найдите, чему равно при этом же
значении
равно 9. Найдите, чему равно при этом же
значении значение выражения: а)
значение выражения: а)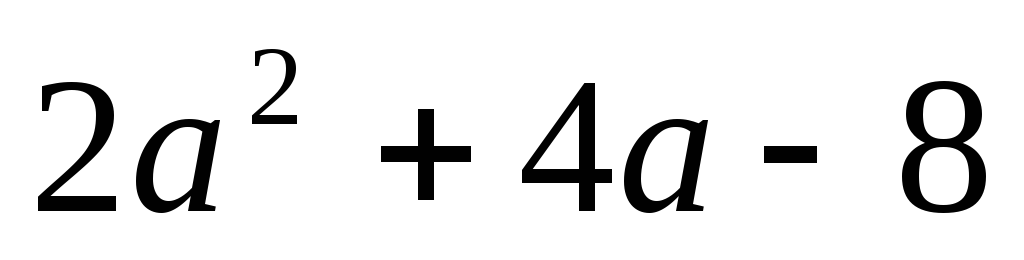 ;
б)
;
б) ;
в)
;
в)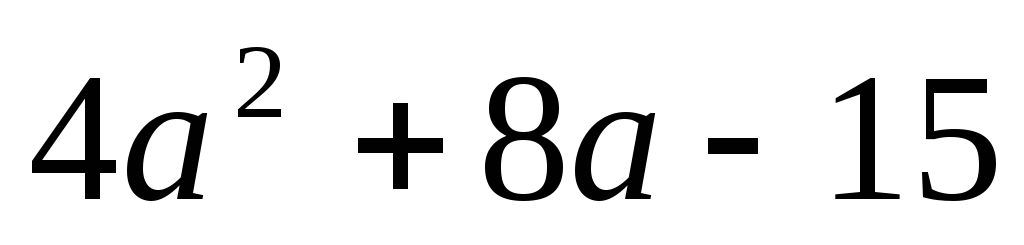 .
.Найдите многочлен
 и вычислите его значение при
и вычислите его значение при ,
если
,
если .
.Разложите на множители выражение: а)
 ;
б)
;
б) .
.Сколько корней имеет уравнение
 при различных значениях параметра
при различных значениях параметра ?
?
Вариант 2
Вынесите за скобку общий множитель: а)
 ;
б)
;
б) ;
в)
;
в) ,
где
,
где ,
, .
.Разложите на множители выражение: а)
 ;
б)
;
б) ;
в)
;
в) ,
где
,
где .
.Найдите значение выражения
 при
при ,
, .
.Известно, что при некотором значении переменной
 значение выражения
значение выражения равно 8. Найдите, чему равно при этом же
значении
равно 8. Найдите, чему равно при этом же
значении значение выражения: а)
значение выражения: а) ;
б)
;
б) ;
в)
;
в) .
.Найдите многочлен
 и вычислите его значение при
и вычислите его значение при ,
если
,
если .
.Разложите на множители выражение: а)
 ;
б)
;
б) .
.Сколько корней имеет уравнение
 при различных значениях параметра
при различных значениях параметра ?
?
Вариант 3
Вынесите за скобку общий множитель: а)
 ;
б)
;
б) ;
в)
;
в) ,
где
,
где .
.Разложите на множители выражение: а)
 ;
б)
;
б) ;
в)
;
в)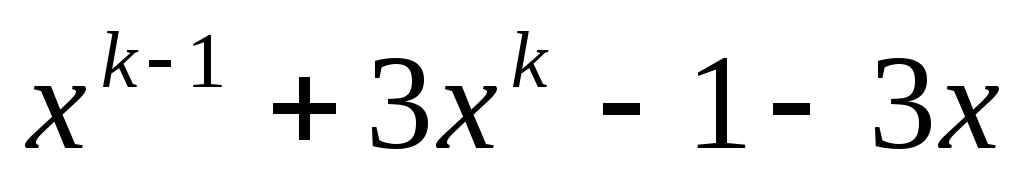 ,
где
,
где .
.Найдите значение выражения
 при
при ,
, .
.Известно, что при некотором значении переменной
 значение выражения
значение выражения равно 2. Найдите, чему равно при этом же
значении
равно 2. Найдите, чему равно при этом же
значении значение выражения: а)
значение выражения: а) ;
б)
;
б) ;
в)
;
в) .
.Найдите значение многочлена
 при
при ,
если
,
если .
.Разложите на множители выражение: а)
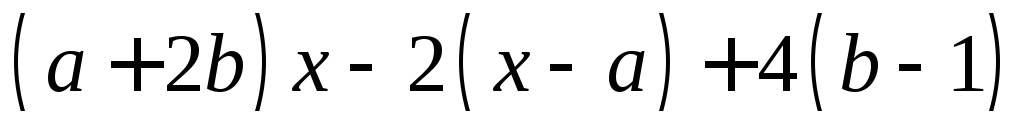 ;
б)
;
б) .
.Найдите корень уравнения
 (а
– параметр) при
(а
– параметр) при
 ,
,
 и
и
 .
Запишите формулу зависимости корней
уравнения от параметра
.
Запишите формулу зависимости корней
уравнения от параметра ,
если
,
если и
и .
.
Самостоятельная работа № 13
§ 10. Применение разложения многочлена на множители
Основные сведения
Произведение
нескольких множителей равно нулю тогда
и только тогда, когда хотя бы один из
них равен нулю, а все другие при этом не
теряют смысл. Если левую часть уравнения
![]() можно разложить на множители
можно разложить на множители![]() ,
где
,
где![]() и
и![]() – многочлены, то данное уравнение
равносильно совокупности уравнений
– многочлены, то данное уравнение
равносильно совокупности уравнений![]() и
и![]() .
.
Подготовительный вариант
Найдите множество корней уравнения: а)
 ;
б)
;
б) ;
в)
;
в) .
.Найдите значение выражения: а)
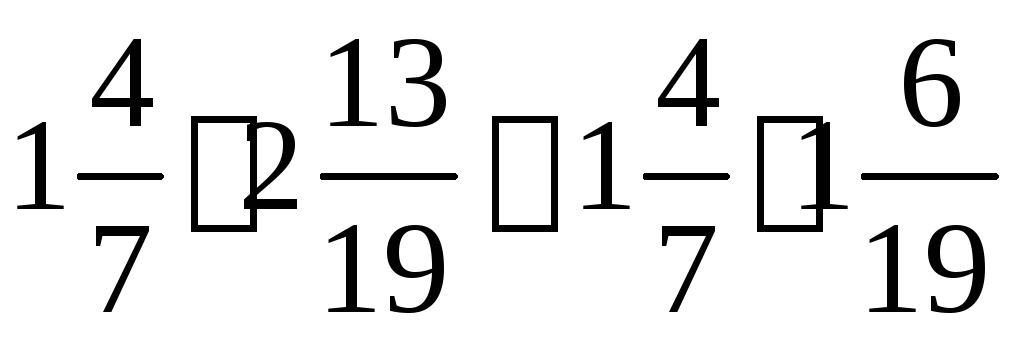 ;
б)
;
б) .
.Докажите, что выражение: а)
 кратно 28; б)
кратно 28; б)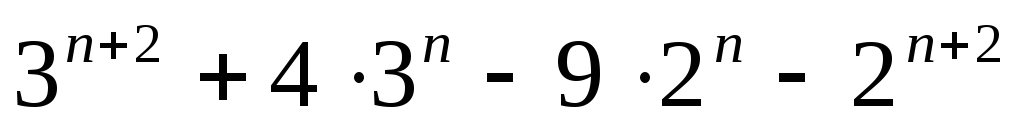 ,
, ,
кратно 13.
,
кратно 13.Решите уравнение: а)
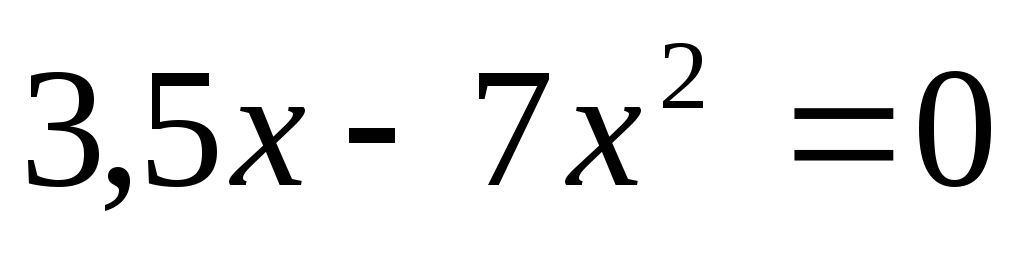 ;
б)
;
б) ;
в)
;
в) .
.При каких значениях переменной выражение: а)
 не имеет смысла; б)
не имеет смысла; б) имеет смысл?
имеет смысл?Найдите общие корни уравнений
 и
и ,
если они существуют.
,
если они существуют.Найдите модуль разности корней уравнения
 .
.
Вариант 1
Найдите множество корней уравнения: а)
 ;
б)
;
б) .
.Найдите значение выражения: а)
 ;
б)
;
б) .
.Докажите, что выражение: а)
 кратно 33; б)
кратно 33; б) ,
, ,
кратно 33.
,
кратно 33.Решите уравнение: а)
 ;
б)
;
б) ;
в)
;
в) .
.При каких значениях переменной выражение: а)
 не имеет смысла; б)
не имеет смысла; б) имеет смысл?
имеет смысл?Найдите общие корни уравнений
 и
и ,
если они существуют.
,
если они существуют.Найдите модуль разности корней уравнения
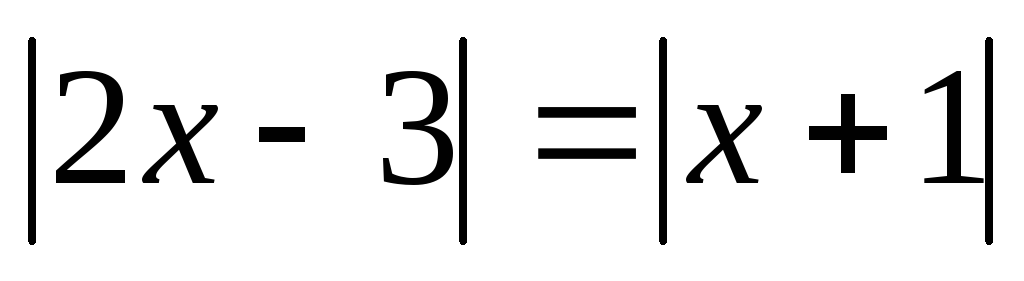 .
.
Вариант 2
Найдите множество корней уравнения: а)
 ;
б)
;
б) .
.Найдите значение выражения: а)
 ;
б)
;
б) .
.Докажите, что выражение: а)
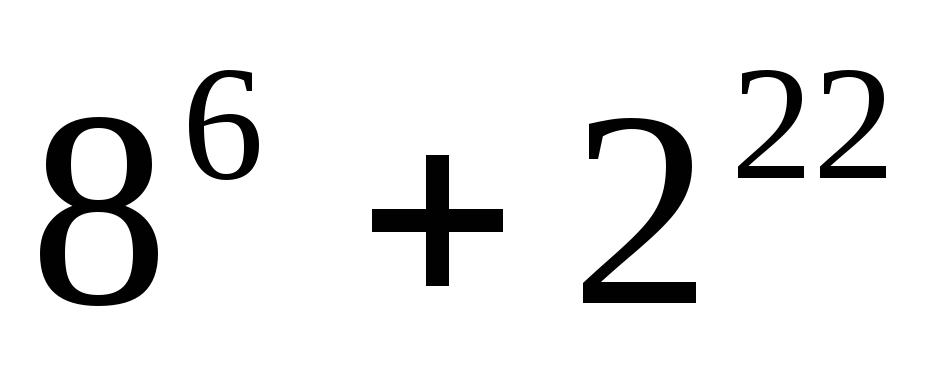 кратно 17; б)
кратно 17; б) ,
,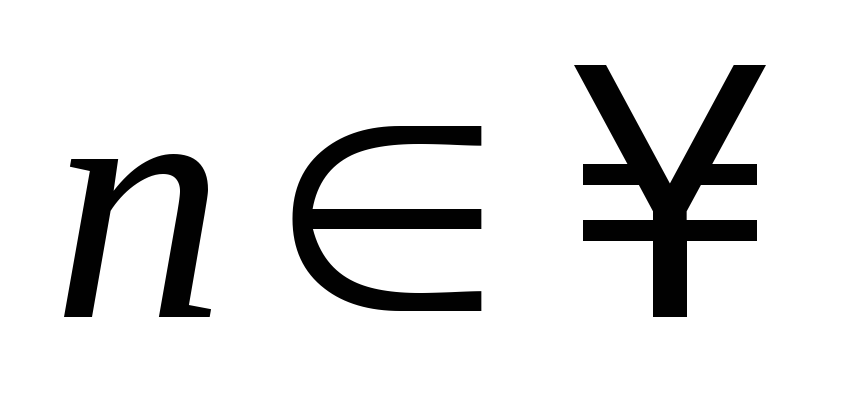 ,
кратно 21.
,
кратно 21.Решите уравнение: а)
 ;
б)
;
б) ;
в)
;
в) .
.При каких значениях переменной выражение: а)
 не имеет смысла; б)
не имеет смысла; б) имеет смысл?
имеет смысл?Найдите общие корни уравнений
 и
и ,
если они существуют.
,
если они существуют.Найдите модуль разности корней уравнения
 .
.
Вариант 3
Найдите множество корней уравнения: а)
 ;
б)
;
б) .
.Найдите значение выражения наиболее рациональным способом: а)
 ;
б)
;
б) .
.Докажите, что выражение: а)
 кратно 13; б)
кратно 13; б) ,
, ,
кратно 31.
,
кратно 31.Решите уравнение, разложив его левую часть на множители: а)
 ;
б)
;
б) ;
в)
;
в) .
.При каких значениях переменной выражение: а)
 не имеет смысла; б)
не имеет смысла; б) имеет смысл?
имеет смысл?Найдите общие корни уравнений
 и
и ,
если они существуют.
,
если они существуют.Найдите модуль разности корней уравнения
 .
.
Самостоятельная работа № 14
§ 11. Разность квадратов
Основные сведения
Произведение
разности двух выражений и их суммы равно
разности квадратов этих выражений, т.е.
![]() .
Это – одна изформул
сокращенного умножения.
Применение тождества
.
Это – одна изформул
сокращенного умножения.
Применение тождества
![]() называютразложением
на множители разности квадратов.
называютразложением
на множители разности квадратов.
Подготовительный вариант
Представьте в виде многочлена выражение: а)
 ;
б)
;
б) ;
в)
;
в)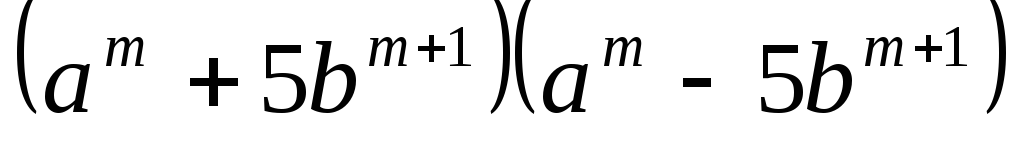 ,
, .
.Разложите на множители выражение: а)
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г) .
.Вычислите значение выражения: а)
 ;
б)
;
б) .
.Решите уравнение: а)
 ;
б)
;
б) .
.Докажите, что выражение
 при любых значениях переменной принимает
лишь положительные значения.
при любых значениях переменной принимает
лишь положительные значения.Найдите множество корней уравнения: а)
 ;
б)
;
б) .
.Сравните числа
 и
и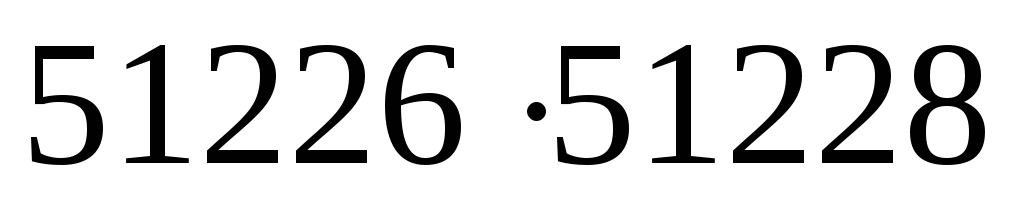 .
.
Вариант 1
Представьте в виде многочлена выражение: а)
 ;
б)
;
б) ;
в)
;
в) ,
, .
.Разложите на множители выражение: а)
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г) .
.Вычислите значение выражения: а)
 ;
б)
;
б) .
.Решите уравнение: а)
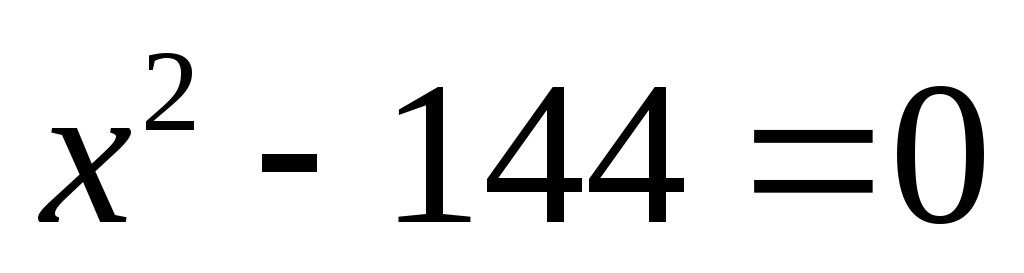 ;
б)
;
б) .
.Докажите, что выражение
 при любых значениях переменной принимает
лишь положительные значения.
при любых значениях переменной принимает
лишь положительные значения.Найдите множество корней уравнения: а)
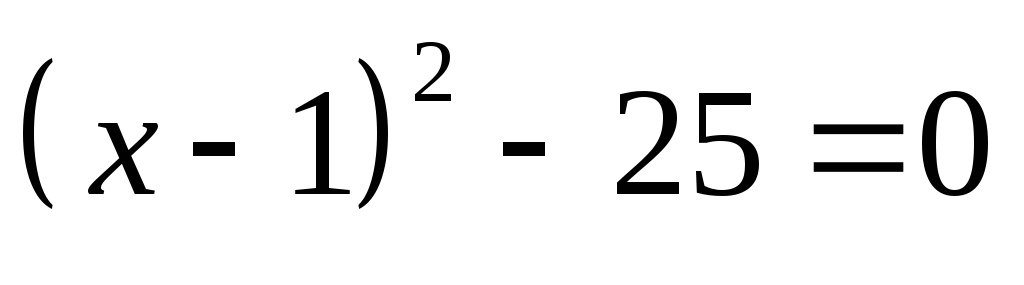 ;
б)
;
б)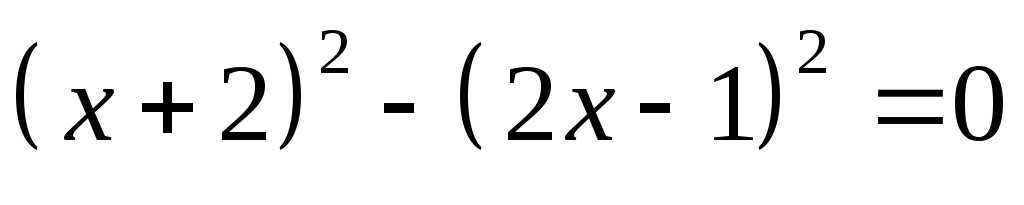 .
.Сравните числа
 и
и .
.
Вариант 2
Представьте в виде многочлена выражение: а)
 ;
б)
;
б) ;
в)
;
в) ,
, .
.Разложите на множители выражение: а)
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г) .
.Вычислите значение выражения: а)
 ;
б)
;
б) .
.Решите уравнение: а)
 ;
б)
;
б) .
.Докажите, что выражение
 при любых значениях переменной принимает
лишь положительные значения.
при любых значениях переменной принимает
лишь положительные значения.Найдите множество корней уравнения: а)
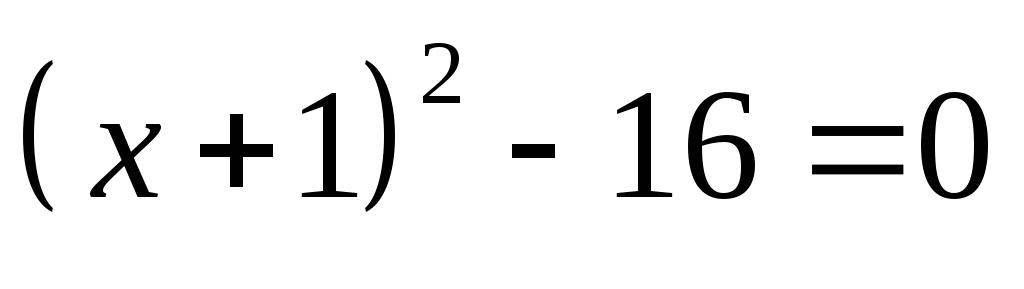 ;
б)
;
б) .
.Сравните числа
 и
и .
.
Вариант 3
Представьте в виде многочлена выражение: а)
 ;
б)
;
б) ;
в)
;
в) ,
, .
.Разложите на множители выражение: а)
 ;
б)
;
б) ;
в)
;
в)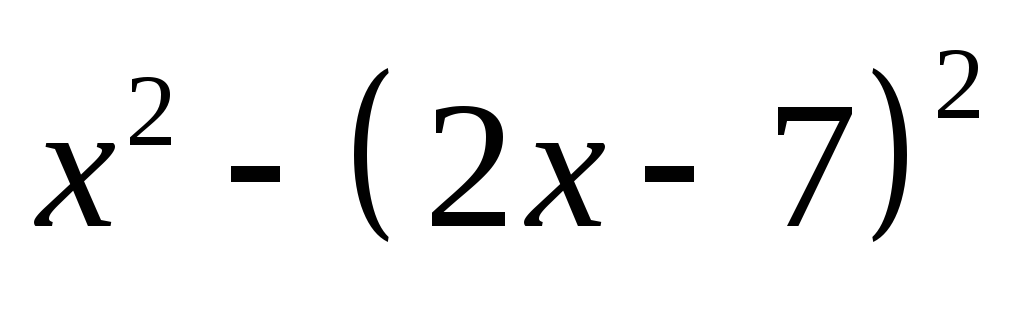 ;
г)
;
г) .
.Вычислите значение выражения: а)
 ;
б)
;
б) .
.Решите уравнение: а)
 ;
б)
;
б) .
.Докажите, что выражение
 при любых значениях переменной принимает
лишь отрицательные значения.
при любых значениях переменной принимает
лишь отрицательные значения.Найдите множество корней уравнения: а)
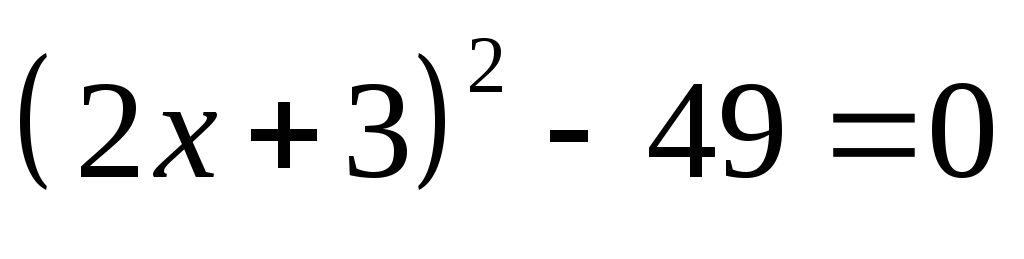 ;
б)
;
б) .
.Сравните числа
 и
и .
.
Самостоятельная работа № 15
§ 12. Квадрат суммы и квадрат разности
Основные сведения
Квадрат суммы двух
выражений равен сумме квадрата первого
выражения, удвоенного произведения
первого и второго выражений и квадрата
второго выражения, т.е.
![]() .
Квадрат разности двух выражений равен
сумме квадратов первого и второго
выражений без удвоенного произведения
первого и второго выражении, т.е.
.
Квадрат разности двух выражений равен
сумме квадратов первого и второго
выражений без удвоенного произведения
первого и второго выражении, т.е.![]() .
Заметим, что
.
Заметим, что![]() .
.
Применение тождеств
![]() и
и![]() называютразложением
на множители квадратных трехчленов
называютразложением
на множители квадратных трехчленов
![]() и
и![]() .
.
Подготовительный вариант
Представьте в виде многочлена выражение: а)
 ;
б)
;
б) ;
в)
;
в)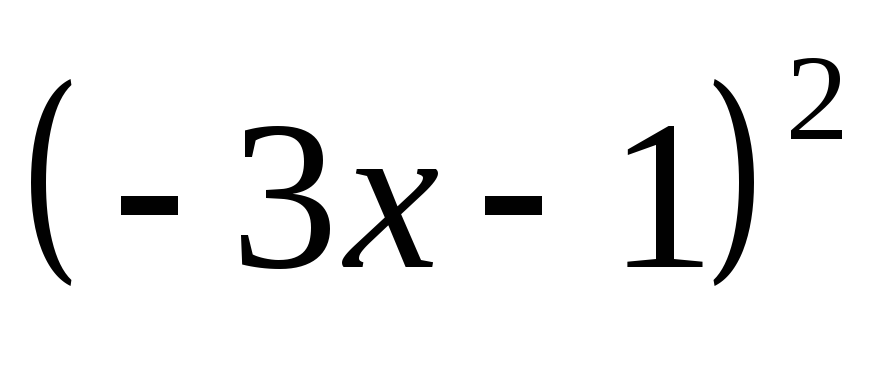 ;
г)
;
г)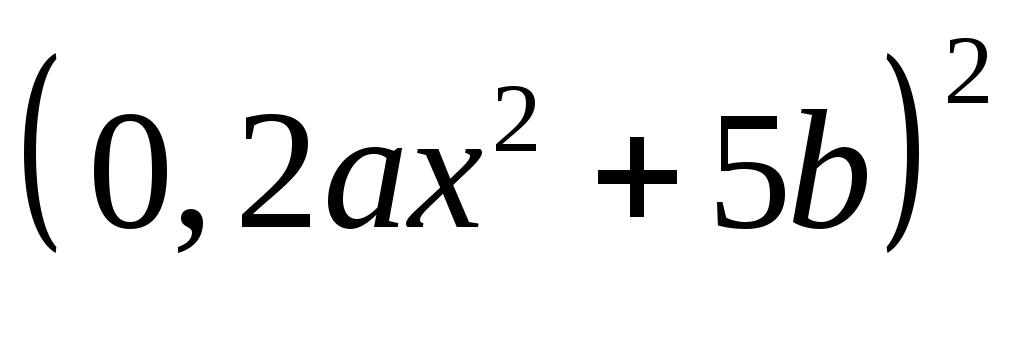 .
.Представьте трехчлен в виде квадрата двучлена: а)
 ;
б)
;
б)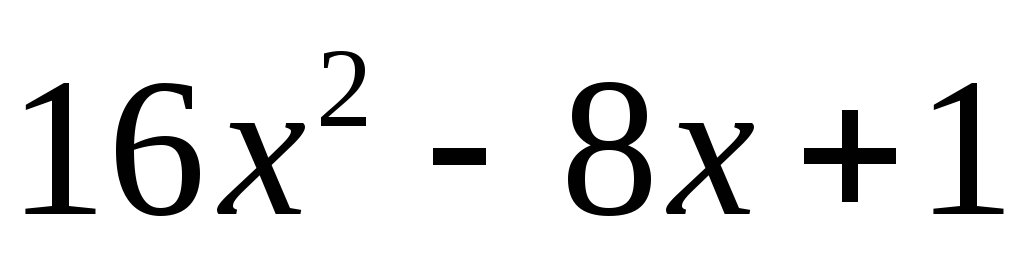 ;
в)
;
в) .
.Найдите множество корней уравнения: а)
 ;
б)
;
б) .
.Найдите значение выражения
 при
при ,
, .
.В выражении
 измените один из коэффициентов так,
чтобы получившийся трехчлен можно было
бы представить в виде квадрата двучлена.
Сколькими способами можно это сделать?
измените один из коэффициентов так,
чтобы получившийся трехчлен можно было
бы представить в виде квадрата двучлена.
Сколькими способами можно это сделать?Решите уравнение
 .
.Докажите, что уравнение
 равносильно уравнению
равносильно уравнению .
.
Вариант 1
Представьте в виде многочлена выражение: а)
 ;
б)
;
б) ;
в)
;
в) .
.Представьте в виде квадрата двучлена: а)
 ;
б)
;
б) ;
в)
;
в) .
.Найдите множество корней уравнения: а)
 ;
б)
;
б) .
.Найдите значение выражения
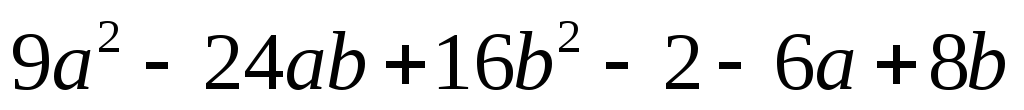 при
при ,
, .
.В выражении
 измените один из коэффициентов так,
чтобы получившийся трехчлен можно было
бы представить в виде квадрата двучлена.
Сколькими способами можно это сделать?
измените один из коэффициентов так,
чтобы получившийся трехчлен можно было
бы представить в виде квадрата двучлена.
Сколькими способами можно это сделать?Решите уравнение
 .
.Докажите, что уравнение
 равносильно уравнению
равносильно уравнению .
.
Вариант 2
Представьте в виде многочлена выражение: а)
 ;
б)
;
б) ;
в)
;
в) .
.Представьте в виде квадрата двучлена: а)
 ;
б)
;
б) ;
в)
;
в) .
.Найдите множество корней уравнения: а)
 ;
б)
;
б) .
.Найдите значение выражения
 при
при ,
, .
.В выражении
 измените один из коэффициентов так,
чтобы получившийся трехчлен можно было
бы представить в виде квадрата двучлена.
Сколькими способами можно это сделать?
измените один из коэффициентов так,
чтобы получившийся трехчлен можно было
бы представить в виде квадрата двучлена.
Сколькими способами можно это сделать?Решите уравнение
 .
.Докажите, что уравнение
 равносильно уравнению
равносильно уравнению .
.
Вариант 3
Представьте в виде многочлена выражение: а)
 ;
б)
;
б) ;
в)
;
в) .
.Представьте в виде квадрата двучлена: а)
 ;
б)
;
б) ;
в)
;
в) .
.Найдите множество корней уравнения: а)
 ;
б)
;
б) .
.Найдите значение выражения
 при
при ,
, .
.В выражении
 измените один из коэффициентов так,
чтобы получившийся трехчлен можно было
бы представить в виде квадрата двучлена.
Сколькими способами можно это сделать?
измените один из коэффициентов так,
чтобы получившийся трехчлен можно было
бы представить в виде квадрата двучлена.
Сколькими способами можно это сделать?Решите уравнение
 .
.Докажите, что уравнение
 равносильно уравнению
равносильно уравнению .
.
Самостоятельная работа № 16
§ 12. Квадрат суммы и квадрат разности
Основные сведения
Квадратным
трехчленом
называется многочлен вида
![]() ,
где
,
где![]() – переменная,
– переменная,![]() – некоторые числа, причем
– некоторые числа, причем![]() .
Число
.
Число![]() называетсястаршим
коэффициентом
квадратного трехчлена,
называетсястаршим
коэффициентом
квадратного трехчлена,
![]() –свободным
членом.
Любой квадратный трехчлен, у которого
старший коэффициент равен 1, можно
записать в виде суммы квадрата двучлена
и некоторого числа, т.е. выделить
из квадратного трехчлена квадрат
двучлена.
Т.е., всегда можно записать
–свободным
членом.
Любой квадратный трехчлен, у которого
старший коэффициент равен 1, можно
записать в виде суммы квадрата двучлена
и некоторого числа, т.е. выделить
из квадратного трехчлена квадрат
двучлена.
Т.е., всегда можно записать
![]() .
.
Подготовительный вариант
Запишите в стандартном виде и укажите: а) старший коэффициент квадратного трехчлена
 ;
б) свободный член квадратного трехчлена
;
б) свободный член квадратного трехчлена .
.Выделите квадрат двучлена из квадратного трехчлена: а)
 ;
б)
;
б) .
.Разложите на множители квадратный трехчлен, выделив квадрат двучлена: а)
 ;
б)
;
б) .
.Решите уравнение, разложив его левую часть на множители с помощью выделения квадрата двучлена и применив формулу разности квадратов двух выражений: а)
 ;
б)
;
б) .
.Докажите, что при любых значениях переменной значение квадратного трехчлена: а)
 положительно; б)
положительно; б) отрицательно.
отрицательно.Найдите: а) наименьшее значение квадратного трехчлена
 ;
б) наибольшее значение квадратного
трехчлена
;
б) наибольшее значение квадратного
трехчлена .
.Дан прямоугольник со сторонами 2 и 14 см. Большую его сторону уменьшили на
 см, а меньшую увеличили на
см, а меньшую увеличили на см. При каком значении
см. При каком значении площадь полученного прямоугольника
будет наибольшей?
площадь полученного прямоугольника
будет наибольшей?
