24

Гидрология 2012

ЛЕКЦИЯ 8. СПЕЦИАЛЬНЫЕ ВОПРОСЫ ГИДРОЛОГИИ РЕК И ВОДОЕМОВ

Вопросы:

1. Движение воды в реках

2. Движение наносов в реках

3. Русловые процессы

4. Термический и ледовый режим рек и водоемов

5. Озера и их морфометрические характеристики

1. Движение воды в реках.

Движение воды в реках происходит под действием силы тяжести при наличии продольного уклона или напора. Скорость течения зависит от соотношения горизонтальной составляющей силы тяжести, определяемой уклоном и разностью напоров, и силы трения, определяемой взаимодействием между частицами внутри потока и частицами и дном.

Для рек характерен турбулентный режим движения воды, отличительной особенностью которого является пульсация скорости или изменение ее во времени в каждой точке по значению и направлению относительно среднего значения.

Вследствие неравномерности потерь по ширине русла скорости течения распре­делены в речном потоке неравномерно: наибольшие скорости на­блюдаются на поверхности потока над наиболее глубокой частью русла, наименьшие - у дна и берегов. В наиболее часто встречающихся условиях закономерном распределении скоростей течения эпюра (график распределения) средних скоростей по глубине речного потока имеет максимум (u_max) вблизи поверхности, скорость, близ­кую к средней на вертикали,- на глубине 0,6h от дна (h - полная глубина) и минимум (u_min), не равный нулю,- у дна (рис. 8.1, а).

Рис. 8.1. Вертикальное распределение скоростей течения в речном потоке:

а -типичное; 6-под ледяным покровом; в - под слоем внутриводного льда (шуги); г - при попутном и встречном ветре; д- при влиянии растительности; е - при влиянии неровностей дна; 1 -ледяной покров; 2-слой шуги; V-направление ветра; u_max - максимальная скорость течения; -и - обратное течение

Однако под влиянием ледяного покрова, ветра, растительности, неровностей рельефа дна и берегов это распределение скоростей нарушается (рис. 8.1, б - e).

Среднюю скорость течения в поперечном сечении v рассчиты­вают по известным расходу воды - Q и площади поперечного сечения -  по формуле: v=Q/.

Наиболее простые закономерности наблюдаются при равномерном движении жидкости в русле, близком к прямолинейному. В этом случае средняя скорость течения в русле может описана формулой Шези.

, (8.1)

где C – коэффициент Шези;

h_ср – средняя глубина в русле, м;

I – уклон водной поверхности.

При сотношении ширины русла (В) и средней глубины (h_ср) менее 10 вместо h_ср используют гидравлический радиус R = / ( - площадь живого сечения, - смоченный периметр).

Коэффициент Шези вычисляют по эмпирическим формулам, среди которых наиболее распространены

формула Маннинга (для рек):

C=h_ср^1/6/n. (8.2)

формула Павловского (для искусственных водотоков – каналов, канав):

C=(1/n) R^y/n (8.3)

y = 0,37+2,5- 0,75(-0,1) ,

где n – коэффициент шероховатости, который находят по специальным таблицам (в России – по таблицам Срибного, Карасева, в США – таблицам Бредли).

Для ровных незаросших русел с песчаным дном п = 0,020 - 0,023; для извилистых русел с неров­ным дном n= 0,023-0,033; для пойм, заросших кустарником, п = 0,033 - 0,045.

Формула Шези показывает, что скорость течения в речном потоке тем больше, чем больше глубина русла и уклон водной поверхности и меньше шероховатость русла.

Путем умножения обеих частей формулы Шези на площадь поперечного сечения  с учетом формулы (8.1) можно получить формулу для определения расхода воды:

. (8.4)

Если морфометрические харак­теристики речного потока изменяются по длине реки, то движение речного потока будет неравномерное и скорость течения будет изменяться вдоль реки. На небольшом участке реки, где расход не меняется из закона сохранения массы вещества можно записать уравнение непрерывности

₁v₁= ₂v₂ = Q=const. (8.5)

Отсюда следует, что увеличение площади поперечного сечения вдоль реки (от створа 1 к створу 2 ) повлечет за собой уменьшение на данном участке скорости течения, как, например, в межень на плесе, уменьшение же площади поперечного сечения вдоль реки приведет к увеличению на этом участке скорости течения, как, например, в межень на перекате.

В случае неравномерного движения уклон водного зеркала уже не будет равен уклону дна, поэтому вдоль реки могут наблюдаться явления подпора (увеличения глубины воды с увеличением расстояния) или явления спада (уменьшения глубины с увеличением расстояния). Причиной неравномерного движения могут быть различные сооружения, возводимые в русле реки – плотины, дамбы, мостовые переходы, спрямление и расчистка русел рек.

Более сложные случаи движения возникают на повороте русла, где наряду с силой тяжести на скорость течения влияет центробежная сила.Это приводит к отклонению течения в поверхностных слоях в сторону вогнутого берега, что создает поперечный перекос уровня воды. В результате избытка гидростатического давления у вогнутого берега в придонных слоях возникает течение, направленное в сторону выпуклого берега. Скла­дываясь с основным продольным переносом воды в реке, разно­направленные течения на поверхности и у дна создают спирале­видное движение воды на изгибе речного русла - поперечную цир­куляцию (рис.8.2).

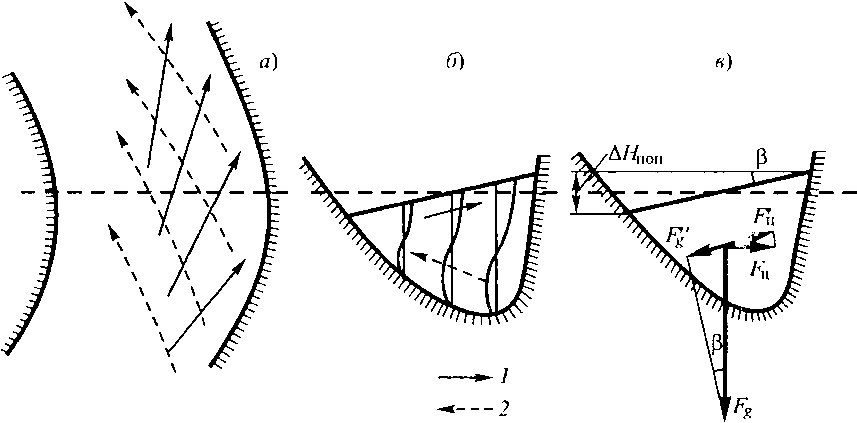
Рис.8.2. Схема поперечной циркуляции на изгибе речного потока в плане (а) и поперечном разрезе (б) и схема действующих сил (в):

1 – поверхностные струи; 2)придонные струи.

Поперечный уклон (I_поп= sin ), который возникает на повороте русла, может определен по формуле

. (8.6)

где v -средняя скорость течения;

g – ускорение свободного падения, м/с2;

r - радиус изгиба русла.

Величина перекоса уровня между обо­ими берегами (H_поп) равна

H_поп= I_попВ, (8.7)

где В- ширина русла.

Пример. При скорости v=1 м/с, r=100 м, B=50 м, величина I_поп=0,001, H_поп=0,05 м.

Наряду с силой тяжести, силой трения и центростремительной силой на частицы жидкости действует отклоняющая сила вращения Земли.

Вследствие суточного вращения Земли с угловой скоростью =2/86400 = 0,0000729 рад/с, всякая материальная точка, движущаяся относительно Земли со скоростью v , испытывает добавочное ускорение ().Сила, соответствующая данному ускорению, называется силой Кориолиса (F_кориол), и равна

F_кориол=m_г=2 mvsin. (8.8)

Сила Кориолиса направлена в северном полушарии под прямым углом вправо к направлению движения частицы, в южном полушарии – влево.

Поперечный уклон, вызываемой силой Кориолиса, равен

I_кориол= v sin/67200, (8.9)

Для северной широты =45 sin=0,707 I_{кориол=} v/95000, при v=1 м/с I_кориол=1,0510^-5. При ширине реки B=50 м перепад уровня H=0,00052 м (0,05 см), что в 100 раз меньше уклона за счет центробежной силы. Наиболее сильно влияние силы Кориолиса проявляется для больших рек (Волга, Днепр, Енисей, Обь и др), что было в свое время обнаружено русским академиком, естествоиспытателем К.Бэром. Однако, из-за своей малости сила Корриолиса, не учитывается в гидравлических расчетах.

2. Движение наносов в реках

Наряду с водой в реках движутся наносы и растворимые примеси. Главными источниками поступления наносов в реки служат поверхность водосборов, подвергающаяся эрозии или процессу разрушения почв и грунтов текущей водой и ветром в период дождей и снеготаяния, и сами русла рек, размываемые речным потоком.

Эрозия поверхности водосборов - процесс сложный, зависящий как от эродирующей способности стекающих по его поверхности дожде­вых и талых вод, так и от противоэрозионной устойчивости почв и грунтов водосбора. Эрозия поверхности водосборов (и поступле­ние ее продуктов в реки) обычно тем больше, чем сильнее дожди и интенсивнее снеготаяние, чем больше неровности рельефа, рых­лее грунты (наиболее легко подвергаются эрозии лёссовые грунты), менее развит растительный покров, сильнее распаханность скло­нов. Эрозия речных русел тем сильнее, чем больше скорости тече­ния в реках и менее устойчивы грунты, слагающие дно и берега. Часть наносов поступает в русло рек при абразии (волновом раз­рушении) берегов водохранилищ и речных берегов на широких плесах. Наносы, слагающие дно рек, называют донными отложени­ями, или аллювием.

Наиболее важные характеристики наносов следующие:

• геомет­рическая крупность, выражающаяся через диаметр частиц наносов (D мм);

• гидравлическая крупность, т. е. скорость осаждения частиц наносов в неподвижной воде (w, мм/с, мм/мин);

• плотность частиц (р_н, кг/м³), равная для наиболее распространенных кварцевых песков2650 кг/м³;

• плотность отложений (плотность грунта) (р_отл, кг/м³), зависящая от плотности частиц и пористости грунта согласно формуле (плотность илистых отложений на дне рек обычно составляет в среднем 700-1000 кг/м³, песчаных 1500-1700, сме­шанных 1000-1500 кг/м³);

• концентрация (содержание) наносов в потоке, которую можно представить как в относительных величинах (отношение массы или объема наносов к массе или объему воды), гак и в абсолютных величинах; в последнем случае используют понятие мутность воды (s, г/м³, кг/м³), которая вычисляется по формуле

s = m/V, (8.10)

где m- масса наносов в пробе воды; V- объем пробы воды. Мутность определяют путем фильтрования отобранных с помощью питометров проб воды и взвешивания фильтров.

Наибольшую концентрацию наносов (мутность воды) имеют реки с паводочным режимом и протекающие в условиях засушливого климата и легкоразмываемых грунтов. Самые мутные реки на Зем­ле - Терек, Сулак, Кура, Амударья, Ганг, Хуанхэ. Средняя годовая мутность рек Терека, Амударьи и Хуанхэ в условиях естественного режима составляла, например, 1,7; 2,9 и 25,8 кг/м³ соответственно. В половодье мутность воды Хуанхэ достигала 250 кг/м³! В насто­ящее время мутность перечисленных рек стала заметно меньше. Для сравнения приведем данные о средней годовой мутности воды в Волге в ее низовьях: до зарегулирования реки она была равна около 60 г/м³, а после зарегулирования уменьшилась до 25-30 г/м³.

По характеру перемещения в реках наносы разделяют на два основных типа - взвешенные и влекомые. Промежуточным типом являются сальтирующие наносы, движущиеся скачкообразно в при­донном слое; наносы этой промежуточной группы условно объеди­няют с влекомыми.

Влекомые наносы - это наносы, перемещающиеся речным пото­ком в придонном слое и движущиеся скольжением, перекатывани­ем или сальтацией. Путем влечения по дну перемещаются наиболее крупные частицы наносов (песок, гравий, галька, валуны).

Таким образом, критерием начала движения влекомых наносов в реках является условие

(8.11)

где u_дно - фактическая придонная скорость течения.

Между «начальной скоростью» и объе­мом или весом перемещающихся частиц:

F_g~D'~u⁶_дно0. (8.12)

Эта формула получила название закона Эри, утверждающего, что вес влекомых наносов пропорционален шестой степени скорости течения. Из формулы Эри следует, что увеличение скорости тече­ния, например в 2, 3, 4 раза, приводит к увеличению веса переме­щающихся по дну частиц наносов соответственно в 64, 729, 4096 раз. Это как раз и объясняет, почему на равнинных реках с малыми скоростями течения поток может переносить по дну лишь песок, а на горных с большими скоростями — гальку и даже огромные валуны. Для перемещения по дну песка необходимы придонные скорости течения не менее 0,10-0,15 м/с, гравия - не менее 0,15- 0,5, гальки - 0,5-1,6, валунов - 1,6-5 м/с. Средняя скорость по­тока должна быть еще больше.

Влекомые наносы могут перемещаться по дну рек либо сплош­ным слоем, либо в виде скоплений, т. е. дискретно. Второй харак­тер движения для рек наиболее типичен. Скопления влекомых наносов представлены донными грядами различного размера (рис. 8.3). Наносы перемещаются слоем по верховому склону гряды и скатываются по низовому склону (его наклон близок к углу естественного откоса) в подвалье гряды. Здесь частицы наносон могут быть «захоронены» надвигающейся грядой и вновь придут в движение лишь после смещения гряды на всю ее полную длину.

Рис.8.3. Донные гряды на дне реки в два последовательных момента времени (1 и 2).

Взвешенные наносы переносятся в толще речного потока. Усло­вием такого перемещения служит соотношение

u⁺_{z }w, (8.13)

где u⁺_z - направленная вверх вертикальная составляющая вектора скорости течения в данной точке потока; w - гидравлическая круп­ность частицы наносов.

Важнейшие характеристики при дви­жении взвешенных наносов в реках - это мутность воды s, определяемая по формуле (8.10), и расход взвешенных наносов:

R=10^-3sQ, (8.14)

где R в кг/с, s в г/м³, Q в м³/с.

Взвешенные наносы распределены в речном потоке неравномерно: в при­донных слоях мутность максимальна и уменьшается по направлению к по­верхности, причем для взвешенных на­носов более крупных фракций быстрее, для наносов мелких фракций - медлен­нее.

Наряду со стоком воды в гидрологии определяют сток наносов.Сток наносов реки включает сток взвешенных и сток влекомых наносов, причем главная роль обычно принадлежит взвешенным наносам. Считается, что на долю влекомых наносов приходится в среднем лишь 5-10% стока взвешенных наносов рек, причем с увеличением размера реки эта доля, как правило, уменьшается.

Предельный суммарный расход как взвешенных, так и влеко­мых наносов, которые может при данных условиях переносить река, называют транспортирующей способностью потока R_тр. Согласно теоретическим и экспериментальным исследованиям R_тр зависит прежде всего от скоростей течения и расхода воды:

(8.15)

где s_тр - мутность воды, соответствующая транспортирующей спо­собности потока;

v -средняя скорость потока;

h_cp - средняя глубина;

w- средняя гидравлическая крупность частиц наносов.

В нашей стране и за рубежом предложено много разных формул вида (8.15). При этом мутность воды s_тр, соответствующую транс­портирующей способности потока (т. е. предельно возможную мут­ность при данных гидравлических условиях), часто выражают как функцию средней скорости течения: s_rp = avⁿ, где а и n - парамет­ры, причем n изменяется от 2 до 4.

В реальных условиях фактический расход наносов в реке и транспортирующая способность потока могут не совпадать, что и становится причиной русловых деформаций.

Сток наносов реки (прежде всего взвешенных наносов) обычно рассчитывают по построенным на основе измерений связям расхо­да воды и расхода взвешенных наносов R=f(Q). У такой связи имеются две важные особенности: она нелинейна, причем R растет быстрее, чем Q; очень приближенно эту зависимость иногда можно записать в виде степенного уравнения:

R = kQ^m, (8.15)

где, по Н. И. Маккавееву, n = 2  3.

Очень часто связь между R и Q оказывается неоднозначной (петлеобразной). Это объясняет­ся несовпадением изменения в реках расходов воды и расходов наносов во времени (рис. 6.18). Максимальная мутность воды в ре­ках (и максимальные расходы наносов тоже) обычно опережают максимальный расход воды, поскольку наиболее активный смыв грунтов с поверхности водосбора идет в период подъема паводка или половодья.

Рис. 8.4. Типичные графики изменения расходов воды и взвешенных наносов (а) и связи между ними (б): 1 - подъем половодья; 2 -спад половодья

С помощью графика связи R=f(Q) по известным средним су­точным значениям Q легко определить и соответствующие величи ны R.

Средние расходы наносов за любой период R определяют точно так же, как и средние расходы воды. Сток наносов рассчитывают по формуле:

W_н = RT, (8.16)

где сток наносов W_н, кг; средний расход наносов R, кг/с; интервал времени T, с.

Сток наносов чаще удобнее представить не в кило­граммах, а в тоннах или даже в миллионах тонн. В этих случаях применяют формулы

W_н (т)= RT 10^-3, (8.17)

Если речь идет о годовых величинах, то записы­вают

W_н (млн т) = R 31,510^-3. (8.18)

Модулем стока наносов называют сток наносов в тоннах с 1 км² площади водосбора (A):

M_H=Wн/A. (8.19)

Для годовых величин стока наносов получим М_н, т/км²:

М_н= R31,510³/F. (8.20)

Модуль стока наносов характеризует эрозионную деятельность речных потоков (напомним, однако, что фактическая денудация в бассейнах рек во много раз больше модуля стока наносов, рас­считанного только что описанными способами, так как огромное количество смытых со склонов наносов не попадает в реки, а от­лагается у подножья склонов, в устьях балок, оврагов, малых при­токов, на поймах.

Модуль стока взвешенных наносов и средняя мутность воды рек, так же как и модуль стока воды, неравномерно распределены по территории. Так, на севере Европейской территории России (тундра, лесная зона) он часто не превышает 1-2 т/км² в год, в северной и западных частях Европейской равнины повышается до 10-20 т/км². На юге Европейской территории бывшего СССР он достигает 50-100 т/км², а в ряде районов Кавказа - даже 500 т/км² в год. Для бассейнов некоторых рек мира модуль стока взвешенных наносов в естественных условиях стока составлял: у Волги - 10,3 т/км², Дуная- 63,6, Терека - 350, Хуанхэ- 1590 т/км² в год. Мутность рек довольно закономерно распределяется по территории. Так, например, средняя годовая мутность рек на севере Европейской части России весьма невелика – 10-50 г/м³, в бассейнах Оки, Днепpa, Дона увеличивается до 150-500 г/м³, на Северном Кавказе иногда превышает 1000 г/м³.

Из суммарного годового стока наносов всех рек мира (15700 млн. т) наибольшая доля в естественных условиях приходится на Амазонку (1200 млн т), Хуанхэ (1185 млн т), Ганг с Брахмапутрой (1060 млн т), Янцзы (471 млн т), Миссисипи (400 млн т) (см. табл. 6.1). Среди наиболее мутных рек на планете - Хуанхэ (средняя годовая мутность воды более 25 кг/м³, а максимальная - в 10 раз больше), Инд, Ганг, Янцзы, Амударья, Терек.