2. Активные фильтры фнч и фвч второго порядка.
На основании выражения (6), запишем в общем виде передаточную функцию фильтра нижних частот второго порядка:
A ( P ) = A 0 / (1 + a 1 P + b 1 P 2 ) (24)
Как следует из выражения, оптимальные передаточные функции второго порядка характеризуются наличием комплексно - сопряженных полюсов. Такие передаточные функции не могут быть реализованы с помощью пассивных RC - цепей. Один из способов реализации подобных фильтров состоит в применении индуктивностей. На рис.18 приведена схема пассивного фильтра нижних частот второго порядка. Запишем передаточную функцию этого фильтра:
A ( P ) = 1 / ( 1 + Wc R C P + Wc 2 L C P 2 )
Для расчета значений R, L и С с учетом (24), получим следующие формулы:
R = a 1 / ( 2 fc ) и L = b 1 / ( 4 2 fc 2 · C )
Для примера рассчитаем ФНЧ типа Баттерворта с частотой среза fc = 10 Гц. Для этого типа фильтра коэффициенты равны a 1 = 1,414 и b 1 = 1,0 (см. Приложение 2). Задав емкость конденсатора С = 10 мкФ и частоту среза fc = 10 Гц, на основании приведенных выше расчетных формул, получим R = 2,25 кОм и L =25,3 Гн. Известно, что такой фильтр очень трудно реализовать из-за большой величины индуктивности. Избежать применения таких индуктивностей можно, используя их аналоги в виде активных RC - цепей.
Рассмотрим две наиболее часто встречающиеся схемы активных фильтров второго порядка.
На рис.19 приведена структурная схема фильтра со сложной отрицательной обратной связью.
Составив уравнения узловых потенциалов для узлов А и В, проведя соответствующие преобразования и решив полученное уравнение относительно передаточной характеристики, получим:
(25)
Сравнивая выражение (25) с передаточной функцией ФНЧ второго порядка (24), нетрудно заметить, что для того, чтобы числитель не был функцией р, в качестве Y 1 и Y 4 должны использоваться резистивные проводимости; для того, чтобы получить член с р 2 в знаменателе, в качестве Y 3 и Y 5 должны использоваться емкостные проводимости; для того, чтобы получить в знаменателе член, независимый от р, в качестве Y 2 должна использоваться резистивная проводимость.
Итак, однозначно определяются пассивные элементы схемы на рис.19: Y 1 = 1 / R 1 , Y 2 = 1 / R 2 , Y 3 = p C 1 , Y 4 = 1 / R 3 , Y 5 = p C 2 .
Cхема полученного ФНЧ приведена на рис.20. Передаточная характеристика имеет вид
Приведем полученную передаточную характеристику к виду передаточной функции ФНЧ второго порядка (24), введя нормированную комплексную переменную (p = P · Wc) и умножив числитель и знаменатель на (R 2 · R 3):
Приравняв коэффициенты этой передаточной функции коэффициентам выражения (24), получим:
A 0 = - R 2 / R 1
a 1 = Wc C 2 [ R 2 + R 3 + ( R 2 R 3 ) / R 1 ] (26)
b 1 = Wc 2 C 1 C 2 R 2 R 3
Как видно из выражения для коэффициента передачи А 0, он имеет отрицательное значение, поэтому прошедший через фильтр низкочастотный сигнал будет инвертирован.
При расчете схемы удобнее задавать значение емкостей и вычислять необходимые значения сопротивления. Поэтому решив уравнение (26) относительно сопротивлений и учитывая, что Wc = 2 fc, получим следующие расчетные формулы:
(27)
Для того, чтобы значение сопротивления R2 было действительным, должно выполняться условие
(28)
При выполнении этого условия в процессе расчета фильтра не следует выбирать отношение С1 / С2, много большим величины, стоящей справа.
На рис.21 приведена структурная схема фильтра с положительной обратной связью.
Составив уравнения узловых потенциалов для узлов А и В, проведя соответствующие преобразования и решив полученное уравнение относительно передаточной характеристики, получим
(29)
На основании аналогичных рассуждений можно показать, что ФНЧ получается из структурной схемы на рис.21, если в качестве Y1 и Y3 использовать резистивные проводимости, а в качестве Y2 и Y4 - емкостные проводимости, т. е. Y1 = 1 / R1, Y2 = pC 1, Y3 = 1 / R2, Y4 = pC2. Схема полученного фильтра нижних частот приведена на рис.22. Передаточная характеристика схемы имеет вид
Приведем полученную передаточную характеристику к виду передаточной функции ФНЧ (24), введя нормированную комплексную переменную p = P Wc и умножив числитель и знаменатель на R1R2:
Приравняв коэффициенты этой передаточной функции к коэффициентам выражения (22), получим:
A0 = 1
a1 = WcC2(R1 + R2) ( 30 )
b1 = Wc 2R1R2C1C2
Считая, что емкости конденсаторов С1 и С2 заданы, получим
(31)
Чтобы значения R1 и R2 были действительными, должно выполняться условие
(32)
Как и в случае фильтра со сложной отрицательной обратной связью, не следует выбирать отношение С1 / С2 много большим значения правой части неравенства.
Если поменять местами емкости и сопротивления в схемах ФНЧ со сложной отрицательной обратной связью (рис.20) и ФНЧ с положительной обратной связью (рис.22), то получим ФВЧ второго порядка.
На рис.23 приведена схема ФВЧ со сложной отрицательной обратной связью. Передаточная функция для этой схемы:
Сравнивая последнее выражение с передаточной функцией ФВЧ второго порядка, получим
A 0 = - C 1 / C 2
a 1 = ( C 1 + C2 + C 3 ) / Wc R 2 C 2 C 3
b 1 = 1 / ( R 1 R 2 C 2 C 3 Wc 2 )
Cчитая, что емкости С 2 и С 3 заданы и равны (С 2 = С 3 = С), получим расчетные формулы для элементов схемы :
C 1 = A 0 C
R 2 = ( A 0 + 2 ) / ( a 1 2 fc C ) ( 33 )
R 1 = a 1 / b 1 ( A 0 + 2 ) C
На рис.24 приведена схема ФВЧ с положительной обратной связью. Передаточная функция для этой схемы:
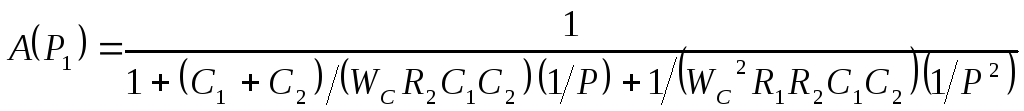
Считая, что емкости С 1 и С 2 заданы и равны (С 1 = С 2 = С), получим следующие расчетные формулы:
A 0 = 1
R 2 = 1 / fc C a1 (34)
R 1 = a1 / 4 fc C b 1