
- •I. Численные методы интегрирования
- •1.1. Интегрирование методом левых прямоугольников
- •1.2. Интегрирование методом правых прямоугольников
- •1.3. Интегрирование методом средних прямоугольников
- •1.4. Интегрирование методом Эйлера
- •1.5. Интегрирование методом Симпсона
- •1.6. Интегрирование методом Монте-Карло
- •II. Численное решение нелинейных уравнений
- •2.1. Метод последовательных приближений (Метод простых итераций)
- •2.2. Метод деления отрезка пополам (Метод дихотомии)
- •2.3. Метод Секущих
- •2.4. Метод касательных (Ньютона-Рафсона)
- •III. Решение системы линейных алгебраических уравнений
- •3.1. Решение слау методом Гаусса
- •3.2. Решение слау методом Гаусса-Жордана
- •3.3. Решение слау методом Крамера
- •3.4. Итерационный метод решения системы линейных
- •3.5. Решение системы нелинейных уравнений
- •IV. Приближение нелинейной функции
- •4.1. Приближение линейной функции
- •4.2. Линейная регрессия общего вида
- •4.3. Интерполяция полиномом Лагранжа
- •4.4. Интерполяция с помощью сплайн-функции
- •V. Обыкновенные дифференциальные уравнения
- •5.1. Метод Эйлера решения обыкновенного
- •5.2. Метод Рунге-Кутта четвертого порядка
- •5.3. Методы прогноза и коррекции
- •5.4. Решение систем дифференциальных уравнений
5.1. Метод Эйлера решения обыкновенного
дифференциального уравнения первого порядка
Пусть дано
дифференциальное уравнение
![]() и
начальное условие
и
начальное условие![]() .
Надо найти такую функцию
.
Надо найти такую функцию![]() ,
которая удовлетворяла бы как
дифференциальному уравнению, так и
начальному условию.
,
которая удовлетворяла бы как
дифференциальному уравнению, так и
начальному условию.
Выбирают число x
настолько малым, чтобы для всех x
в интервале (x0,x1),
где
![]() ,
значения функции мало отличались от y0
(функция
непрерывна). Тогда для указанного
интервала изменения x
можно производную в левой части
дифференциального уравнения заменить
на близкое ей по величине отношение
конечных приращений зависимой и
независимой переменной:
,
значения функции мало отличались от y0
(функция
непрерывна). Тогда для указанного
интервала изменения x
можно производную в левой части
дифференциального уравнения заменить
на близкое ей по величине отношение
конечных приращений зависимой и
независимой переменной:
![]() .
.
Из полученного соотношения выражают формулу, по которой находят y:
![]() ,
,
где
![]() есть значение производнойy
в точке
есть значение производнойy
в точке
![]() .
Иными словами, на этом участке кривая
заменяется отрезком прямой (касательной
к ней в начале участка).
.
Иными словами, на этом участке кривая
заменяется отрезком прямой (касательной
к ней в начале участка).
Таким образом, при заданных значениях x0 и y0 можно вычислить искомое значение функции, двигаясь с малым шагом по x вплоть до заданного значения:
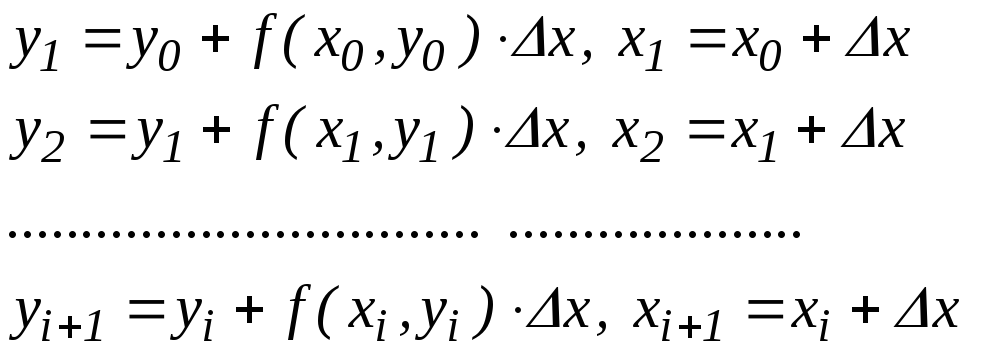 . (5.5)
. (5.5)
Г
 еометрический
смысл метода Эйлера представлен на
рис.5.1. Ошибка определенияy
прямо пропорциональна длине шага и
будет тем меньше, чем меньше выбрана
длина шага x.
еометрический
смысл метода Эйлера представлен на
рис.5.1. Ошибка определенияy
прямо пропорциональна длине шага и
будет тем меньше, чем меньше выбрана
длина шага x.
Из уравнения (5.3) можно записать:
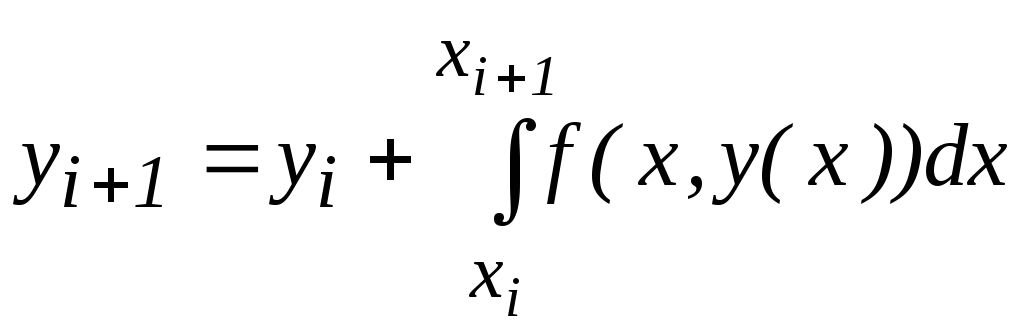 .(5.6)
.(5.6)
Если в интеграле
(5.6) функцию
![]() принять постоянной и равной значению
в точкеxi,
то величина интеграл будет равна
принять постоянной и равной значению
в точкеxi,
то величина интеграл будет равна
![]() ,
так что формула (5.6) обращается в формулу
(5.5).
,
так что формула (5.6) обращается в формулу
(5.5).
Метод Эйлера не
всегда дает практически требуемой
точности вычислений, однако некоторая
модификация алгоритма вычислений
повышает точность искомых результатов.
Рассмотрим вновь дифференциальное
уравнение (5.3) с начальным условием
(5.4). Если опять принять функцию
![]() постоянной и равной
постоянной и равной![]() ,
но равной значению функции не в начале,
а в середине участка.
,
но равной значению функции не в начале,
а в середине участка.
Учитывая, что теперь x1 является серединой отрезка (x0,x2), можно найти значение y2 по формуле:
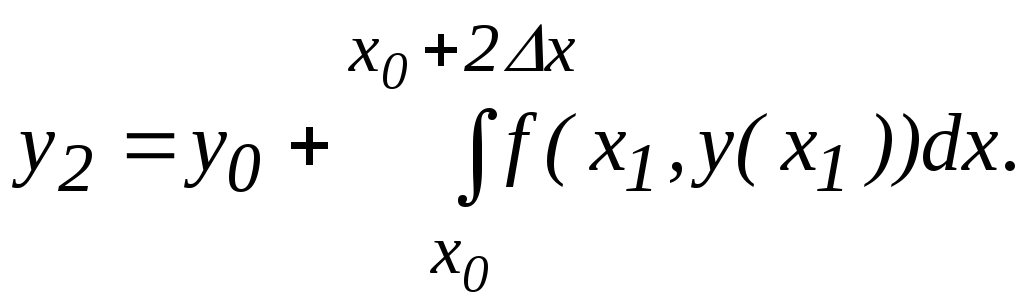
Так как
![]() ,
то
,
то![]() .
По найденному значению
.
По найденному значению![]() находят
находят![]() ,
после чего можно найти
,
после чего можно найти![]() ,
рассматривая участок (x1,x3)
и т.д.
,
рассматривая участок (x1,x3)
и т.д.
Таким образом, получают формулу улучшенного метода Эйлера для i 1:
![]() (5.7).
(5.7).
По этой формуле нельзя, однако, отыскать y1. Для его нахождения используют соотношение (5.5).
5.2. Метод Рунге-Кутта четвертого порядка
для решения уравнения первого порядка
Методы Рунге-Кутта обладают следующими отличительными признаками: 1) одноступенчатые; 2) согласуются с радом Тейлора до членов порядка hP, где P – степень, различная для различных методов и называется порядком метода, а h = x – расстояние между точками; 3) не требуют вычисления производных, а требуют только вычисления значений самой функции. Следует отметить, что рассмотренный ранее метод Эйлера является одним из методов Рунге-Кутта первого порядка, так как он согласуется с разложением в ряд Тейлора вплоть до членов порядка h.
Одним из наиболее часто используемых методов интегрирования дифференциальных уравнений является метод Рунге-Кутта четвертого порядка. Из-за своего широкого применения его просто называют методом Рунге-Кутта. Для случая решения дифференциального уравнения первого порядка (5.3) этот метод сводится к следующим соотношениям:
![]() ,
,
где
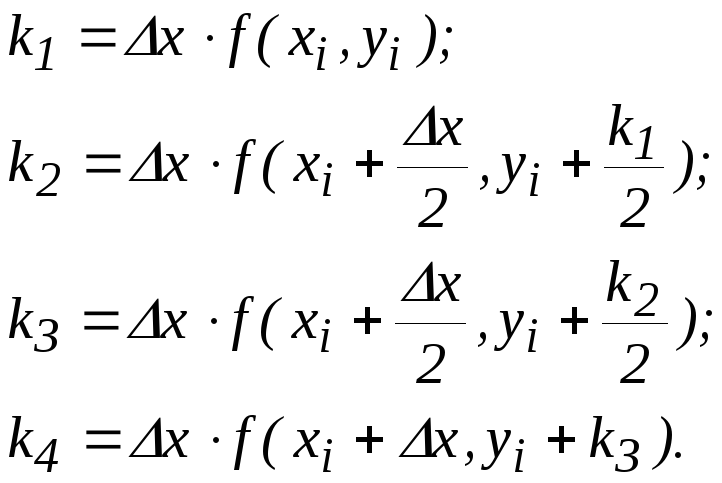
Решение уравнения
методом Рунге-Кутта приводит к уменьшению
ошибки вычисления значения функции в
точке x.
Ошибка метода прямо пропорциональна
четвертой степени шага по x:
![]()
