
- •Для студентов 3го курса физического факультета
- •1. Закон Кулона
- •2. Определение напряженности электрического поля
- •3. Определение напряженности магнитного поля
- •4. Закон Ампера
- •5. Плотности заряда и тока
- •6. Закон сохранения заряда в дифференциальной форме
- •7. Силовые линии и эквипотенциальные поверхности
- •8. Градиент, дивергенция, ротор. Оператор набла
- •9. Законы электромагнетизма
- •11. Уравнения Пуассона-Лапласа для электро- и магнитостатического полей
7. Силовые линии и эквипотенциальные поверхности
Силовая линиявекторного поля![]() – линия, в каждой точке которой вектор
– линия, в каждой точке которой вектор![]() направлен по касательной к ней. Уравнение
силовых линий в произвольной ортогональной
системе координат имеет вид:
направлен по касательной к ней. Уравнение
силовых линий в произвольной ортогональной
системе координат имеет вид:
![]() (7.1)
(7.1)
где
![]() – коэффициенты Ламе.
– коэффициенты Ламе.
Силовые линии всегда перпендикулярны
к эквипотенциальным поверхностям.
Силовые линии не пересекаются, т.к. в
противном случае поле
![]() было бы неоднозначно заданным.
было бы неоднозначно заданным.
8. Градиент, дивергенция, ротор. Оператор набла
8.1. Градиент скалярного поля![]() – вектор, задающий направление наибольшего
роста функции
– вектор, задающий направление наибольшего
роста функции![]() и численно равный скорости роста в этом
направлении. В произвольной ортогональной
системе координат
и численно равный скорости роста в этом
направлении. В произвольной ортогональной
системе координат![]() задается выражением:
задается выражением:
![]() . (8.1)
. (8.1)
8.2. Дивергенция векторного поля![]() в точке
в точке![]() – плотность потока векторного поля
– плотность потока векторного поля![]() через произвольную замкнутую поверхность
через произвольную замкнутую поверхность![]() ,
охватывающую точку
,
охватывающую точку![]() :
:
 . (8.2)
. (8.2)
Здесь
![]() – объем, охватываемый поверхностью
– объем, охватываемый поверхностью![]() .
.
Физический смысл: плотность скалярных источников векторного поля
 .
.Геометрический смысл: мера расходимости силовых линий поля
 .
.
В произвольной ортогональной системе координат:
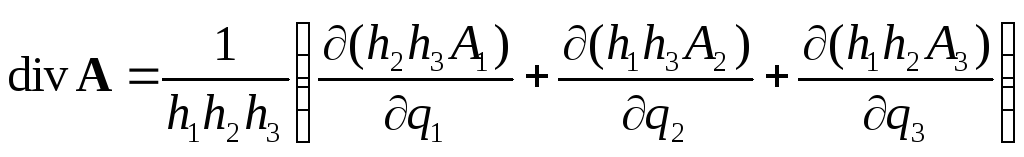 (8.3)
(8.3)
8.3. Роторвекторного поля![]() в точке
в точке![]() – это вектор, проекция которого на
направление
– это вектор, проекция которого на
направление![]() определяется поверхностной плотностью
циркуляции векторного поля
определяется поверхностной плотностью
циркуляции векторного поля
![]() :
:
 . (8.4)
. (8.4)
где
![]() – замкнутый контур, лежащий в плоскости,
перпендикулярной вектору
– замкнутый контур, лежащий в плоскости,
перпендикулярной вектору![]() ,
,![]() – площадь участка поверхности,
ограниченной контуром
– площадь участка поверхности,
ограниченной контуром![]() .
.
Физический смысл:
 – плотность векторных источников поля
– плотность векторных источников поля .
.Геометрический смысл:
 – мера завихренности силовых линий
поля
– мера завихренности силовых линий
поля .
.
В произвольной ортогональной системе координат
 . (8.5)
. (8.5)
8.4. Оператор набла в произвольной ортогональной системе координат имеет вид:
![]() . (8.6)
. (8.6)
Свойства:
а)
![]() – оператор дифференцирования:
– оператор дифференцирования:
![]() ;
;
b)
![]() – вектор.
– вектор.
Основные операции:
a)![]() ;
;
b)![]() ;
;
c)![]() .
.
Вид оператора набла в
ДСК:
![]() . (8.7)
. (8.7)
ЦСК:
![]() (8.8)
(8.8)
ССК:
![]() (8.9)
(8.9)
9. Законы электромагнетизма
9.1. Теорема Гаусса-Остроградского о свойствах электрического поля
Поток вектора напряженности
![]() электрического полячерез
произвольную замкнутую поверхность
электрического полячерез
произвольную замкнутую поверхность![]() пропорционален величина заряда
пропорционален величина заряда![]() ,
находящегося в объеме
,
находящегося в объеме![]() ,
ограниченном этой поверхностью:
,
ограниченном этой поверхностью:
![]() .
.
Здесь
![]() ,
,![]() – вектор нормали к поверхности.
Коэффициент
– вектор нормали к поверхности.
Коэффициент![]() соответствует системе СГС.
соответствует системе СГС.
9.2.Закон Фарадея об электродвижущей силе
Работа по перемещению единичного
точечного положительного заряда вдоль
замкнутого контура называется
электродвижущей силой:![]() .
Контурный интеграл
.
Контурный интеграл![]() – циркуляция вектора напряженности
электрического поля. В электростатике
– циркуляция вектора напряженности
электрического поля. В электростатике![]() (условие потенциальности электрического
поля).
(условие потенциальности электрического
поля).
Циркуляция вектора напряженности
![]() изменяющегося электрического
полявдоль замкнутого контура
изменяющегося электрического
полявдоль замкнутого контура![]() пропорциональна скорости изменения
магнитного потока
пропорциональна скорости изменения
магнитного потока![]() через произвольную поверхность
через произвольную поверхность![]() ,
натянутую на этот контур:
,
натянутую на этот контур:
![]() ,
,
где
![]() .
.
9.3. Закон Гаусса об отсутствии магнитных зарядов
Поток вектора напряженности ![]() магнитного полячерез произвольную
замкнутую поверхность равен нулю:
магнитного полячерез произвольную
замкнутую поверхность равен нулю:
![]() .
.
9.4.1. Закон Био-Савара-Лапласа для статического магнитного поля (циркуляционная теорема)
Циркуляция вектора напряженности
![]() магнитного поля вдоль
замкнутого контура
магнитного поля вдоль
замкнутого контура![]() пропорциональна току, протекающему
через произвольную поверхность
пропорциональна току, протекающему
через произвольную поверхность![]() ,
натянутую на этот контур:
,
натянутую на этот контур:

Здесь
![]() – число линейных проводников, проходящих
через поверхность
– число линейных проводников, проходящих
через поверхность![]() .
.
9.4.2. Закон Био-Савара-Лапласа-Максвелла для изменяющегося магнитного поля
Циркуляция вектора напряженности ![]() изменяющегося магнитного
поля вдоль замкнутого контура
изменяющегося магнитного
поля вдоль замкнутого контура![]() пропорциональна сумме токов зарядов и
«токов смещения», протекающих через
произвольную поверхность, натянутую
на этот контур:
пропорциональна сумме токов зарядов и
«токов смещения», протекающих через
произвольную поверхность, натянутую
на этот контур:
![]() (для распределенных токов),
(для распределенных токов),
где
![]() ,
,
![]() – вектор напряженности электрического
поля.
– вектор напряженности электрического
поля.
10. Уравнения Максвелла электромагнитного поля в вакууме
 (10.1)
(10.1)
Уравнения Максвелла, фактически,
представляют собой задание явного вида
скалярных (![]() и
и![]() )
и векторных (
)
и векторных (![]() и
и![]() )
источников электрического и магнитного
полей.
)
источников электрического и магнитного
полей.
Граничные условия (общий вид):
 (10.2)
(10.2)
Здесь
![]() и
и![]() – плотности поверхностных зарядов и
токов соответственно, индексы
– плотности поверхностных зарядов и
токов соответственно, индексы![]() ,
,![]() и
и![]() обозначают нормальные (
обозначают нормальные (![]() )
и тангенциальные (
)
и тангенциальные (![]() ,
,![]() )
составляющие к поверхности раздела
)
составляющие к поверхности раздела![]() и
и![]() .
Единичные векторы
.
Единичные векторы![]() ,
,![]() и
и![]() связаны между собой соотношением:
связаны между собой соотношением:
![]() . (10.3)
. (10.3)
Граничные условия в ДСК:

 (10.4)
(10.4)
Уравнения электростатического поля:
![]() ,
,![]() . (10.5)
. (10.5)
Уравнения магнитостатического поля:
![]() ,
,![]() . (10.6)
. (10.6)
