Вступ до аналізу. Ч. 1

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесский национальный университет им. И.И. Мечникова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2 , * " 2 * *

.pdf

Скачиваний:

Добавлен:

20.05.2015

Размер:

1.42 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

#. ! .

. * + *-

. + , " m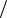 n , m, n . & 2 -

, " ', 1, , "

', 2, :

1 2 3						4		5 L n L
1		2		3		4				5			L		n	L

2		2		2		2		2						2
1		2		3		4			5			L		n		L

3		3		3		3		3						3
1		2		3		4				5			L		n	L

4		4		4		4		4						4
. . .
1		2		3		4					5		L		n	L

	n		n		n		n				n				n

…

" ! * ' * ( , 1, 2 , 3 ). 6 '

2 3

, " ( ! 5, , ''

!, , * + * -

. 6 * + ’, * * " -

. / + * , !’, " + -

* , + ’, * + {0}. .

( 2 3 , * + *-

7. .

. + , . % +, , ,

+ ( , + * (0,1) , ' ,.

". ! (0,1) .

. + ( (0,1) + !

" " !, ! . # ! , - ":

0, α1α2α3 Kαn K ,

! αk ". (, " αk ,

, 0, " (0,1) *. + +,

" ! ( 9, !

. . : 0,5 = 0, 49999... = 0, 4(9) .

+. %, ( -

(0,1) , ' + '. # + ( -

(0,1) * , , -

*. .( n , 0, αn1αn 2αn3 Kαnn K (0,1) . % !-

, 0,β1β2β3 Kβn K , 0 < βk < 9, βk ≠ αkk . # ,

+ 0, αk1αk 2αk 3 Kαkk K (k = 1, 2,...) , * ", * "

* ( ,' ' ( αkk ). 0,β1β2β3 Kβn K – + (

(0,1) , ( , * . / (2

". ) + + ( (0,1) , '.

. * " +, + + ( -

(0,1), , * " + ' + ( . continuum – *).

# +, +, ' * " -

+ , , !’, " * ! ! (. 6 " . 5 ,, + ! * "

! , + , " ( + +

( ) ' * + * . % + *

' * + + , .

4 " – ' * +, + * " ! ! + '

+ ' ? 0 , , " " , , -

+ . 4" , * " .

8. , .

6 2 * , ,' ( + 2

, " , ! , " + * (-

! * " " " +. 6 " + " " -

* + y 2 x : y = f (x) .

5 x ', * ", , +, !

' " y .

. (, , y = x2 . 8 (, , " x ( , ",

, -2, -1, 0, 1, 2, y ( " 4, 1, 0, 1, 4.

% , x ( , ", " ! + ' * "

" . 0 ": " ! * - ! + " " y ?

	. 2 ( " " ’" , * " + . .(
,' y = x2			" x ! + ' * " 1. # -
, " y + ! * ! + " 1. . :

x		0		0,5	0,75	0,9	0,95	0,99

y		0		0,25	0,5625	0,81	0,9025	0,9801

#, " y ! * ! + ", !, " + * , "-

1, " ! + , "

y = x2 x = 1. ( “ ” + , * " +. $" ':

y= x2 −1 . x −1

0 + ": " " ! " y

," x " , 1?

( + x = 1, * ,

! ( :

0 .

" " y x = 1 (*

" ,), + " , " " , y , " x * 1 ( ', 1). * x ≠ 1, ! x −1 ≠ 0 , 2 * ' x2 − 1 = ( x − 1)( x + 1) , , 2

x −1, ,, " x ≠ 1 :

y= x + 1.

!, " x 1 y " , 1+1=2.

# !, " , " " " , -

y , " x " , " x0 , + ’"

* , y x0 . # -

" ' * y = f (x) " xx0 . , " " , ". # -

" +.

6 +, * , " y = f (x)

x0 , " x0 + , "

( . .( :

1, x ≠ 0, y =

0, x = 0.

. + +, " y " x 0 ',

1. & ( + " y x = 0 ', 0.

. + " ,. . " y = sin	1	, " ! -
	x

2, , " x 0.

6 ! ' ! ' " '

" . & ' ! '

2 – ", . (

2 " ’" " + "

, * ! ’" π . 0 ' -

’" : * ( -

, ! ( ! ( .

14). & ' ( Sn	+ ( n – -
), ! + :
Skp ≈ n Sn .	(8.1)

. * " ? & 2, ! *2 n , !

2 ", * " . )! ' !- *2 ! *2 " n , ! ! *2 "

$ . 14.

, * ! ! *2 n (8.1),

+ ,. " " ? " * !

( ' n Sn , " n " , . # !

( ' ! + ! *2-

. 4" ", " + . 27, ', πR2 , R –

. 4 ( , " .

. ! * ! " * , + -

. .( , M , " , * " +

". .( t " (2 *s . &, "

2 * ( " 2 " ! ', * " ':

v = s .

*. $ " t M - + " : , , 2, *,

( " , 2 (!

! , * " * "). # "

2 * , * ' ' . # -

, + " 2 " " * ,! * " ( , ! *. 5 +

(? 5 ' " * 2 v " - + t ". & +, " *

( + 2 " * – " " . & " * 2 -

– .

. 5 + * n -

* ( * ( xn , + -

{x1, x2 ,..., xn ,...} ' * (! -

0 2 * – + (-

% 2 ( ' * " + 2 *

!. . , + * {1, 2, 3,..., n,...} ', -

* – + * n *

. 0 2 ,

{a, a + d , a + 2d ,..., a + (n −1)d ,...} {b, bq,bq2 ,...,bqn−1,...} -

& xn , * " . 4 , " ! * " * n ", (

n . . ,	" * xn = n , "
x	= a + (n − 1)d , " x = bqn−1 .
n	n

. * ( * .

1) 1,	1	,	1	,	1	,...,	1	,...;	x =	1	,

4		9		16			n2		n	n2

							1 + (−1)n						1 + (−1)n
2)	0,1, 0,1, 0,1,...,									,...;			x =		,
2)	0,1, 0,1, 0,1,...,									,...;			x =		,
								2					n	2
								2						2
3)	3, 3, 3,..., 3,...;								xn = 3 ,
4)		1	,	2	,	3	,...,	n	,...;	x	=	n	,
4)			,		,		,...,		,...;	x	=		,
	5 25 125							5n		n		5n
	5 25 125							5n				5n
5)		1, 2, 6, 24,120, 720,..., n!,...;										xn = n!.
	. , , n! ( n - ) –													! *
1 n , ! n! = 1 2 3Ln .

? + ( . recurrens – () !. * ( , ' * " *

( m ) , * " , " -

m + ( ( .

. > ! ' * " :

x1 = x2 = 1, xn = xn−1 + xn−2 (n = 3, 4,...)

# ! + , ' *, ', . 0 ' ' , * " ( * ( -

, + +. & " ' * " (

, " " " *.

*2 *, , * ( xn , ! -

: {xn } .

. % * {xn } , * " !, " -

, M , n : xn ≤ M .

. % * {xn } , * " , " ,

m , n : xn ≥ m .

. % * {xn } , * " , " !-

+ .

# , * ! +, " ! + + -

. " ! + ,: M > 0 , n :

| xn | ≤ M .

., * xn = −n ! + ( ! + -), * xn = n ! + ( ! + ), -

* xn = 1 n2 ! +.

. % * {xn } , * " ( ),

" n : xn +1 > xn ( xn +1 ≥ xn ).

# ! + , ' , ! *2 ( 2)

. % * {xn } , * " ( ), " n : xn +1 < xn ( xn +1 ≤ xn ).

# ! + , ' , 2 ( ! *2)

	.,						* x = n2 – ',	* x = 2−n –
							n	n
,				* {1,1, 2, 2,3,3, 4, 4,...} –				, *
	1	1 1 1
1,1,		,	,		,	,... – '.

	2	2 3 3
	6 ', , ' ' * " -
".
	. , {xn } { yn } , * " -
*		{xn + yn }					(+ , ',

( {xn } { yn } ).

' * " ", ! - (.

9. % & .

% ( ! * " " . $ -

" * n + 1 & ( " ( "

. , -

' * * 2 , .

$ . 15.

/ !, " n ! +- ' * " 1. $" (0,8;1, 2) , " ( *

1. 4 ( , 0,2– 1, x (0,8;1, 2) -


*			x − 1	< 0, 2 .
	# + 2 ! + " 2 -
						1. ),		2 5
	3	4			5	6		+ * ( -
	2;	= 1,5;			≈ 1,33;	= 1, 25;	= 1, 2

	2	3			4	5
,, + 1,2						* + *). " 2

, ' 2	7	;	8	;	9	;...	, "' * " (,

	6		7 8

+ " ! *:

xn − 1

< 0, 2

(9.1)

/ + , " 0,2 (2 " N = 5 (, ,

' , ! n > N = 5 , -

! * * " * (9.1).

# " 2 (, ! *2 * ( 1, (0, 9;1,1) , !-0,1– 1. 0 " * , * " ",

(. 4* 2 10 2	2;	3	,...,		11


		2		10

+ *, 2, ' 11-

;

; ... , -

11 12

+ *, " *

xn − 1

< 0,1

n > 10 .

, " ", , 0,01– 1, !

+ x , * ", * | x −1| < 0, 01, , ,

, N = 100 ,

102 103

"' * * , ( + -

,...

101 102

! * xn − 1 < 0, 01 n > 100 .

# + " *. 5 ! +

x = 1, + ( * " ( N (, ' -

, " * *

(! * *), ( + ! " 2

* * . 2 " -

N ' 5, 10, * 100. & - + *? ) + 2 – + " ,

, +, ! ! *2 N . . !

+ , , ( + ', 2ε , ε –

, ! " ε - x = 1. " x *

| x −1| < ε .

# + ( : ' ,

N = [1 ε]		( [x] – x )
x =	n + 1	! * + (1 − ε,1 + ε) . # , N , -

n	n

		29

+, + * ε , " ( , + . # !

ε > 0 N = N (ε) (! N , + * ε ) (, n > N -

*: xn − 1 < ε .

* + *, 1 , ' {xn }

n → ∞ , 2 *:

lim x = lim			n + 1	= 1.

n→∞	n	n→∞	n

(lim – " limes – ").

+ ' " -

* :

. ? x0 , * " {xn } , " "

! * " ε ( * " ( N , " ( + *

ε , " n , ! *2, + N , , * " *:

xn − x0 < ε .

6 ' " , * " :

? x0 , * " {xn } , "

ε > 0 N (ε) n > N : xn − x0 < ε .

* 2:

lim xn = x0 .

n→∞

0 2 , ,, ! * ", *

x0 ( * " * * ,

+ * 2 , * " 2 * *.

5 * , ', , * " ,

+ – .

.
1. $" *, ! xn	= c . % +, lim xn = c .
	n →∞

6 * ε > 0 . ), * | xn − c | < ε , * " " ! * " n , + " N + " 1.

2. , lim x								(−1)n
2. , lim x							= lim 3 +			= 3 .
				n→∞		n		n	2
				n→∞			n→∞		2
6 * ε > 0 ":

	x − 3	=	(−1)n	=	1	.
			(−1)n		1

	n		n2		n2
			n2		n2

& " :

< ε .

# n

, !

n >

. ) +, " N =

, " -

, '

N + 1, ! :

xn − 3

< ε . # -

4 ( ,,

ε > 0 N =

: n > N

xn − 3

< ε .

lim xn

= 3 .

n→∞

3. , lim x = lim

3n − 5

n→∞

n→∞ 2n + 7

6 * ε > 0 ":

x −

3n − 5

−

6n −10 − 6n − 21

+ 7 2

2(2n + 7 )

2(2n + 7)

4n + 14

< ε ,

n >

−

# , "

4n + 14

4ε

N =

−

, ,

N + 1,

4ε

xn −

< ε . ) + ε > 0 N =

−

n > N :

xn −

< ε , ( ! !

4ε

4. , * {1; −1;1; −1; ... ; (−1)n−1 ;...} , "

6 * (

= (−1)n−1 . %,

lim xn

= x0 . #

ε > 0 N (ε)

n > N :

xn − x0

< ε .

)!,

n→∞

ε= 1 . #, ' N + 1, ! : 2

− x

$" " ( m > N . #

xm − xm+1

= 2 , * ! * " -

"' * " 2. 6 2 !:

− x

= 1.

x − x

x − x + x − x

≤

x − x

m+1

0 0

m+1

# * 2 < 1. 4 ( ,, -

, .

/ + * ! , " ' * ', " " -

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.2018110.08 Кб4восточн_Aziya.doc
#
20.05.20151.43 Mб22ВСЕ ВОПРОСЫ ПО ИСТОРИИ ЭКОНОМИКИ.doc
#
01.05.2025144.31 Кб0ВСЕ ОТВЕТЫ.docx
#
20.05.20153.47 Mб76Всемирная история.pdf
#
12.08.201955.98 Кб2всесв. 10 кл. СРСР.docx
#
20.05.20151.42 Mб4Вступ до аналізу. Ч. 1.pdf
#
20.05.20151.45 Mб4Вступ до аналізу. Ч. 2.pdf
#
20.05.201520.47 Кб16ВСТУП.docx
#
01.04.2025102.91 Кб0вступление в фармакологию.doc
#
01.03.2025235.69 Кб3вся философия.docx
#
01.07.2025397.13 Кб0вся экология.docx