
- •Перелік питань до іспиту з «Алгебри та геометрії» для студентів 1 курсу спец. «комп’ютерна інженерія» 2014-2015 н.Р.
- •Свойства определителей
- •Треугольные матрицы
- •Диагональные матрицы
- •2.10. Приведение матрицы к диагональному виду
- •Ступенчатая матрица
- •Алгоритм приведения матрицы к ступенчатому виду
- •Свойства Инвариантность ранга при элементарных преобразованиях
- •Эквивалентность слау при элементарных преобразованиях
- •Нахождение обратных матриц
- •Ступенчатый вид по строкам
- •Определитель произведения матриц Теорема 2.2 об определителе произведения матриц
- •Обратная матрица
- •Замечание
- •Свойства обратной матрицы:
- •Матричные уравнения
- •Понятие комплексного числа
- •Действительная и мнимая часть комплексного числа
- •Мнимая единица
- •Равные комплексные числа
- •1.2.Тригонометрическая форма комплексного числа.
- •Формулы для многочленов и операции над многочленами
- •2. Деление с остатком. Теорема Безу
- •Нахождение нод по алгоритму Евклида и с помощью разложения на простые множители.
- •Алгоритм Евклида для нахождения нод
- •Нахождение нод с помощью разложения чисел на простые множители
- •Нахождение нод трех и большего количества чисел
- •Нахождение нод отрицательных чисел
- •Кратные корни многочленов
- •Метод Штурма отделения корней многочлена
- •Способы разложения на множители многочлена степени выше второй.
- •Вынесение за скобки общего множителя.
- •Разложение на множители многочлена с рациональными корнями.
- •Гипотеза h
- •Формулировка
- •Частные случаи
- •*4. Основная теорема алгебры
- •Линейные пространства: определение и примеры Аксиомы линейного пространства
- •Следствия аксиом линейного пространства
- •Примеры линейных пространств
- •Изоморфизм линейных пространств
- •Пересечение и сумма подпространств линейного пространства
- •Прямая сумма подпространств
- •Признаки прямых сумм подпространств
- •Формулы скалярного произведения векторов заданных координатами
- •Примеры задач на вычисление скалярного произведения векторов Примеры вычисления скалярного произведения векторов для плоских задач
- •Пример вычисления скалярного произведения векторов для пространственных задач
- •Пример вычисления скалярного произведения для n -мерных векторов
- •Векторное произведение векторов и его свойства
- •Алгебраические свойства векторного произведения
- •Геометрические свойства векторного произведения
- •Выражение векторного произведения через координаты векторов
- •Формула вычисления векторного произведения
- •Определение смешанного произведения.
- •Смешанное произведение в координатной форме.
- •Свойства смешанного произведения.
- •Вычисление смешанного произведения, примеры и решения.
- •Геометрический смысл смешанного произведения.
- •Необходимое и достаточное условие компланарности трех векторов.
- •Уравнение поверхности
- •Уравнение прямой по точке и вектору нормали
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и угловому коэффициенту
- •Уравнение прямой по точке и направляющему вектору
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •Угол между прямыми на плоскости
- •Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
- •Расстояние от точки до прямой
Понятие комплексного числа
Определение
Комплексным
числом называется
выражение вида ![]()
Например. ![]()
Действительная и мнимая часть комплексного числа
Определение
Действительное
число ![]() называется действительной
частью комплексного
числа
называется действительной
частью комплексного
числа ![]() и
обозначается
и
обозначается ![]() (От
французского слова reel -
действительный).
(От
французского слова reel -
действительный).
Действительное
число ![]() называется мнимой
частью числа
называется мнимой
частью числа ![]() и
обозначается
и
обозначается ![]() (От
французского слова imaginaire -
мнимый).
(От
французского слова imaginaire -
мнимый).
Например. Для
комплексного числа ![]() действительная
часть
действительная
часть ![]() ,
а мнимая -
,
а мнимая - ![]() .
.
Если
действительная часть комплексного
числа ![]() равна
нулю (
равна
нулю ( ![]() ),
то комплексное число называется чисто
мнимым.
),
то комплексное число называется чисто
мнимым.
Например. ![]()
Мнимая единица
Величина ![]() называется
мнимой единицей и удовлетворяет
соотношению:
называется
мнимой единицей и удовлетворяет
соотношению:
![]()
Равные комплексные числа
Два
комплексных числа ![]() и
и ![]() называются
равными, если равны их действительные
и мнимые части соответственно:
называются
равными, если равны их действительные
и мнимые части соответственно:
![]()
Пример
Задание. Определить
при каких значениях ![]() и
и ![]() числа
числа ![]() и
и ![]() будут
равными.
будут
равными.
Решение. Согласно
определению ![]() тогда
и только тогда, когда
тогда
и только тогда, когда
![]()
Ответ. ![]()
Число ![]() называется комплексно
сопряженным числом к
числу
называется комплексно
сопряженным числом к
числу ![]() .
.
То есть комплексно сопряженные числа отличаются лишь знаком мнимой части.
Например. Для
комплексного числа ![]() комплексно
сопряженным есть число
комплексно
сопряженным есть число ![]() ;
для
;
для ![]() комплексно
сопряженное
комплексно
сопряженное ![]() и
для
и
для ![]() имеем,
что
имеем,
что ![]() .
.
Комплексное
число ![]() называется противоположным к комплексному
числу
называется противоположным к комплексному
числу ![]() .
.
Например. Противоположным
к числу ![]() есть
число:
есть
число: ![]() .
.
Алгебраическая форма комплексного числа.
В алгебраической форме комплексное
число записывают в виде
 ,
гдеаиb–
вещественные числа. Два комплексных
числа
,
гдеаиb–
вещественные числа. Два комплексных
числа и
и равны
тогда и только тогда, когда
равны
тогда и только тогда, когда ,
, .
На основании этого определения решим
несколько задач.
.
На основании этого определения решим
несколько задач.
Задача 1.1.Найти .
.
Решение.Предположим, что .Тогда
.Тогда или
или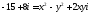 .
Используя условие равенства двух
комплексных чисел, получаем систему
уравнений для определения
.
Используя условие равенства двух
комплексных чисел, получаем систему
уравнений для определения :
:

Решая систему, находим
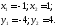
Откуда
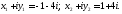
Итак,
 .
.
Задача 1.2.Найти так чтобы
так чтобы .
.
Имеем
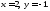
По определению произведением комплексных
чисел
 и
и называется число
называется число
 .
.
Заметим, что комплексные числа можно перемножать как два многочлена первой степени с учетом того, что
 .
.
Оперируя
с комплексными числами, мы нередко
получаем дроби вида
 ,
которые желательно упростить. Для этого
надо умножить числитель и знаменатель
дроби на число, комплексно сопряженное
к знаменателю, то есть
,
которые желательно упростить. Для этого
надо умножить числитель и знаменатель
дроби на число, комплексно сопряженное
к знаменателю, то есть
 .
.
Квадратні рівняння.
Квадратное уравнение — уравнение вида ax2 + bx + c = 0, где a, b, c — некоторые числа (a ≠ 0), x — неизвестное.
Числа ![]() называются
коэффициентами квадратного уравнения.
называются
коэффициентами квадратного уравнения.
 называется
первым коэффициентом;
называется
первым коэффициентом; называется
вторым коэффициентом;
называется
вторым коэффициентом; —
свободным
членом.
—
свободным
членом.
Приведенное
квадратное уравнение —
уравнение вида ![]() ,
первый коэффициент которого равен
единице (
,
первый коэффициент которого равен
единице (![]() ).
).
Если
в квадратном уравнении коэффициенты ![]() и
и![]() не
равны нулю, то уравнение
называетсяполным квадратным
уравнением. Например, уравнение
не
равны нулю, то уравнение
называетсяполным квадратным
уравнением. Например, уравнение ![]() .
Если один из коэффициентов
.
Если один из коэффициентов![]() или
или![]() равен
нулю или оба коэффициента равны нулю,
то квадратное уравнение называетсянеполным.
Например,
равен
нулю или оба коэффициента равны нулю,
то квадратное уравнение называетсянеполным.
Например, ![]() .
.
Значение
неизвестного ![]() ,
при котором квадратное уравнение
обращается в верное числовое равенство,
называется корнем этого уравнения.
Например, значение
,
при котором квадратное уравнение
обращается в верное числовое равенство,
называется корнем этого уравнения.
Например, значение![]() являетсякорнем
квадратного уравнения
являетсякорнем
квадратного уравнения ![]() ,
потому что
,
потому что![]() или
или![]() —
это верное числовое равенство.
—
это верное числовое равенство.
Решить квадратное уравнение — это значит найти множество его корней.
Тригонометрична форма комплексних чисел, їх геометрична інтерпретація.
