
- •Перелік питань до іспиту з «Алгебри та геометрії» для студентів 1 курсу спец. «комп’ютерна інженерія» 2014-2015 н.Р.
- •Свойства определителей
- •Треугольные матрицы
- •Диагональные матрицы
- •2.10. Приведение матрицы к диагональному виду
- •Ступенчатая матрица
- •Алгоритм приведения матрицы к ступенчатому виду
- •Свойства Инвариантность ранга при элементарных преобразованиях
- •Эквивалентность слау при элементарных преобразованиях
- •Нахождение обратных матриц
- •Ступенчатый вид по строкам
- •Определитель произведения матриц Теорема 2.2 об определителе произведения матриц
- •Обратная матрица
- •Замечание
- •Свойства обратной матрицы:
- •Матричные уравнения
- •Понятие комплексного числа
- •Действительная и мнимая часть комплексного числа
- •Мнимая единица
- •Равные комплексные числа
- •1.2.Тригонометрическая форма комплексного числа.
- •Формулы для многочленов и операции над многочленами
- •2. Деление с остатком. Теорема Безу
- •Нахождение нод по алгоритму Евклида и с помощью разложения на простые множители.
- •Алгоритм Евклида для нахождения нод
- •Нахождение нод с помощью разложения чисел на простые множители
- •Нахождение нод трех и большего количества чисел
- •Нахождение нод отрицательных чисел
- •Кратные корни многочленов
- •Метод Штурма отделения корней многочлена
- •Способы разложения на множители многочлена степени выше второй.
- •Вынесение за скобки общего множителя.
- •Разложение на множители многочлена с рациональными корнями.
- •Гипотеза h
- •Формулировка
- •Частные случаи
- •*4. Основная теорема алгебры
- •Линейные пространства: определение и примеры Аксиомы линейного пространства
- •Следствия аксиом линейного пространства
- •Примеры линейных пространств
- •Изоморфизм линейных пространств
- •Пересечение и сумма подпространств линейного пространства
- •Прямая сумма подпространств
- •Признаки прямых сумм подпространств
- •Формулы скалярного произведения векторов заданных координатами
- •Примеры задач на вычисление скалярного произведения векторов Примеры вычисления скалярного произведения векторов для плоских задач
- •Пример вычисления скалярного произведения векторов для пространственных задач
- •Пример вычисления скалярного произведения для n -мерных векторов
- •Векторное произведение векторов и его свойства
- •Алгебраические свойства векторного произведения
- •Геометрические свойства векторного произведения
- •Выражение векторного произведения через координаты векторов
- •Формула вычисления векторного произведения
- •Определение смешанного произведения.
- •Смешанное произведение в координатной форме.
- •Свойства смешанного произведения.
- •Вычисление смешанного произведения, примеры и решения.
- •Геометрический смысл смешанного произведения.
- •Необходимое и достаточное условие компланарности трех векторов.
- •Уравнение поверхности
- •Уравнение прямой по точке и вектору нормали
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и угловому коэффициенту
- •Уравнение прямой по точке и направляющему вектору
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •Угол между прямыми на плоскости
- •Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
- •Расстояние от точки до прямой
Способы разложения на множители многочлена степени выше второй.
В общем случае эта задача предполагает творческий подход, так как не существует универсального метода ее решения. Но все же попробуем дать несколько наводок.
В
подавляющем числе случаев, разложение
многочлена на множители основано на
следствии из теоремы Безу, то есть
находится или подбирается корень ![]() и
понижается степень многочлена на единицу
делением на
и
понижается степень многочлена на единицу
делением на ![]() .
У полученного многочлена ищется
корень
.
У полученного многочлена ищется
корень ![]() и
процесс повторяется до полного разложения.
и
процесс повторяется до полного разложения.
Если же корень найти не удается, то используются специфические способы разложения: от группировки, до ввода дополнительных взаимоисключающих слагаемых.
Дальнейшее изложение базируется на навыках решения уравнений высших степеней с целыми коэффициентами.
Вынесение за скобки общего множителя.
Начнем
с простейшего случая, когда свободный
член равен нулю, то есть многочлен имеет
вид ![]() .
.
Очевидно,
что корнем такого многочлена является ![]() ,
то есть многочлен представим в виде
,
то есть многочлен представим в виде ![]() .
.
Этот способ есть ни что иное как вынесение общего множителя за скобки.
Пример.
Разложить
многочлен третьей степени ![]() на
множители.
на
множители.
Решение.
Очевидно,
что ![]() является
корнем многочлена, то есть х можно
вынести за скобки:
является
корнем многочлена, то есть х можно
вынести за скобки:
![]()
Найдем
корни квадратного трехчлена ![]()

Таким
образом,

К началу страницы
Разложение на множители многочлена с рациональными корнями.
Сначала
рассмотрим способ разложения многочлена
с целыми коэффициентами вида ![]() ,
коэффициент при старшей степени равен
единице.
,
коэффициент при старшей степени равен
единице.
В этом случае, если многочлен имеет целые корни, то они являются делителями свободного члена.
Пример.
Разложить
на множители выражение ![]() .
.
Решение.
Проверим,
имеются ли целые корни. Для этого
выписываем делители числа -18: ![]() .
То есть, если многочлен имеет целые
корни, то они находятся среди выписанных
чисел. Последовательно проверим эти
числа по схеме
Горнера. Ее удобство еще и в том, что
в итоге получим и коэффициенты разложения
многочлена:
.
То есть, если многочлен имеет целые
корни, то они находятся среди выписанных
чисел. Последовательно проверим эти
числа по схеме
Горнера. Ее удобство еще и в том, что
в итоге получим и коэффициенты разложения
многочлена: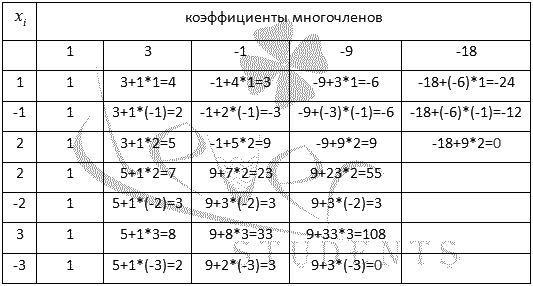
То
есть, х=2 и х=-3 являются
корнями исходного многочлена и он
представим в виде произведения:

Осталось
разложить квадратный трехчлен ![]() .
.
Дискриминант этого трехчлена отрицательный, следовательно, он не имеет действительных корней.
Ответ:
![]() .
.
Замечание:
вместо схемы Горнера можно было воспользоваться подбором корня и последующим делением многочлена на многочлен.
Теперь
рассмотрим разложение многочлена с
целыми коэффициентами вида ![]() ,
причем коэффициент при старшей степени
не равен единице.
,
причем коэффициент при старшей степени
не равен единице.
В этом случае многочлен может иметь дробно рациональные корни.
Пример.
Разложить
на множители выражение ![]() .
.
Решение.
Выполнив
замену переменной y=2x,
перейдем к многочлену с коэффициентом
равным единице при старшей степени. Для
этого сначала домножим выражение на 4.

Если
полученная функция ![]() имеет
целые корни, то они находятся среди
делителей свободного члена. Запишем
их:
имеет
целые корни, то они находятся среди
делителей свободного члена. Запишем
их:
![]()
Вычислим
последовательно значения функции g(y) в
этих точках до получения нуля.

То
есть, y=-5 является
корнем ![]() ,
следовательно,
,
следовательно, ![]() является
корнем исходной функции. Проведем
деление столбиком (уголком) многочлена
является
корнем исходной функции. Проведем
деление столбиком (уголком) многочлена ![]() на
двучлен
на
двучлен ![]() .
.

Таким
образом,
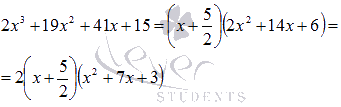
Проверку
оставшихся делителей продолжать
нецелесообразно, так как проще разложить
на множители полученный квадратный
трехчлен ![]()

Следовательно,

Незведені многочлени. Теорема про розклад многочлена у добуток незведених. Канонічний розклад многочлена.
