Исправление моментов времени за планетную аберрацию

Пусть в момент светило находилось в точке , а Земля (геоцентрический наблюдатель) в точке . Свет, вышедший из в момент , дойдёт до наблюдателя в момент , когда наблюдатель будет находиться уже в точке . А – время, в течение которого свет проходит расстояние, равное 1 а.е. (аберрационная постоянная):

,

1 А.Е. Свет пройдет за (499.0s или 8m19.0s).

Наблюдение светила естественно производится в момент или . На самом деле, получаемые координаты светила относятся к моменту или :

, [35]

где A = 0.0057755 сут/а.е.,

- геоцентрическое расстояние светила, выраженное в а.е.

После нахождения 1-го приближения прямоугольных гелиоцентрических координат светила, исправляем время за планетную аберрацию по формулам [35]. Затем по формулам [24] получаем новые значения приведенного времени .

При точном вычислении здесь надо заново интерполировать координаты Солнца .

Теперь в разложениях [27] можно вычислять члены высших порядков и получать с более высокой точностью. Эта идея принадлежит Лагранжу. Гаусс отказался от этого из-за громоздкости вычислений и предложил иной путь вполне строгого нахождения .

Пусть (вспомним [2]) - удвоенные площади секторов между соответствующими радиус-векторами светила. Обозначим, как и выше, отношение площади сектора к площади соответствующего ему треугольника

. [36]

Тогда, домножая отношения площадей треугольников и соответственно на и , получим

Из II-го закона Кеплера (см.[2]) следует, что площади секторов относятся как промежутки времени между наблюдениями, и следовательно,

[37]

Здесь, конечно, надо брать значения приведенного времени , исправленные за планетную аберрацию.

Как только мы найдем , сразу же получим и улучшенные значения (из [37]) и сможем решить систему [12].

Вычисление отношения площади сектора к площади треугольника

Известно (в 1-м приближении) два гелиоцентрических положения тела и время , в течение которого светило перешло из одного положения в другое (время исправлено за планетную аберрацию). Таким образом, известны радиусы-векторы и угол между ними :

Или, лучше (точнее, так как малый угол):

По определению и используя формулу [2]:

[38]

Здесь в правой части неизвестно . Надо его исключить. Сделать это можно при помощи уравнений эллиптического движения.

Отметим, что некоторые величины, являющиеся мнимыми для гиперболы, по завершении преобразований исчезают и конечный результат пригоден для любого конического сечения.

Если - истинная аномалия,

- эксцентрическая аномалия, то, вспоминая равенства, полученные при выводе уравнения Кеплера (см. “ЗАДАЧА 2-х ТЕЛ” [54] и [55]):

можно записать следующее

[39]

[39’]

[40]

[40’]

[41]

[41’]

[42]

[42’]

Проведём следующие преобразования – [39][39’]+[40][40’]

левая часть

правая часть

.

Итак [43]

[39][39’]-[40][40’]

левая часть

правая часть

.

Итак [44]

Из [43] и [44] исключим [44]e+[43]

,

. [45]

Далее, сложим [42] и [42’]:

и подставим сюда [45]:

;

;

;

. [46]

Таким образом, получено значение , которое можно подставить в [38]:

,

из тригонометрии , тогда

,

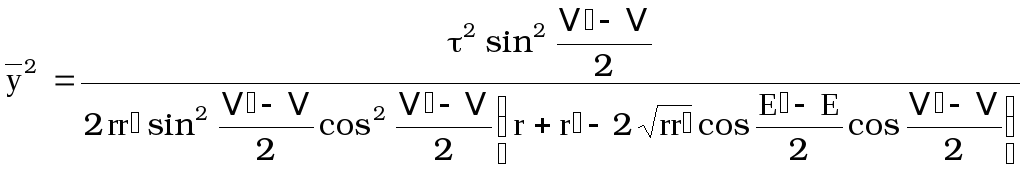. [47]

Введем обозначения [48]

Тогда последнее соотношение можно записать в виде

[ПЕРВОЕ УРАВНЕНИЕ ГАУССА] [49]

Найдем [41’]-[41]:

,

Отсюда надо исключить и . Вспомним [43]:

[43’]

и подставим

,

. [50]

Вспомним, что уравнение эллипса можно записать через эксцентрическую аномалию , тогда

, ,

,

.

Исключая с помощью [43’] :

,

,

.

Вспомним [47]

, [47]

,

и подставим

. [51]

Исключая из [50] с помощью [51], находим

,

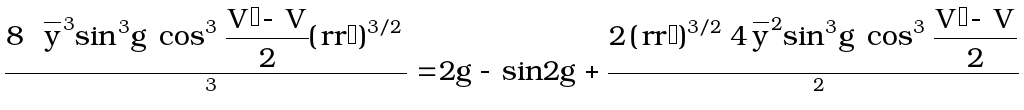
используя обозначения [48]:

,

[ВТОРОЕ УРАВНЕНИЕ ГАУССА] [52]

Для нахождения необходимо решить [49] и [52].

Если , то есть наблюдения близки между собой, то из определения [38] следует, что .

Введём обозначения [53]

Далее из [49] и [52] исключается , выражается через ; и разлагаются в ряды по и после достаточно длинных преобразований:

, [54]

где 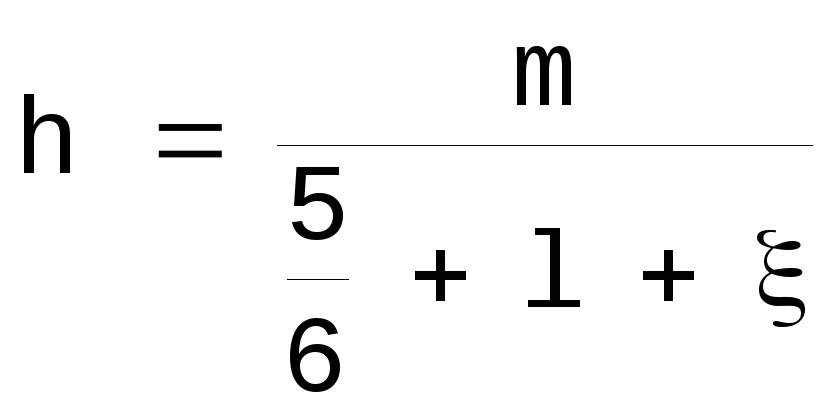, [55]

где [56]

Итак, прежде всего, из [48] находим и ,

затем в [55] полагаем и находим ,

решаем [54] относительно (~1),

из [49] и [53] следует , так что сюда подставляем найденный ,

получаем ,

из [56] находим ,

входим в [55], получаем новое ;

Далее – в [54] и снова получаем ...

Это уже метод нахождения , применимый на практике. На основе этого метода можно записать алгоритм нахождения для наблюдений, разделённых не очень большими промежутками времени:

1 шаг =1.05

2 шаг [49]

3 шаг вычисляем [57]

4 шаг [52]

5 шаг

6 шаг

Вернемся к основной задаче. Величины введены в соотношениях [36]; - в соотношениях [24]. Обозначения [48] для можно представить в виде:

,

где

Тогда

Введём обозначения

,

, [58]

.

Тогда

[59]

Теперь по алгоритму [57] можно вычислить .