Компланарные (тригональные) точки Лагранжа

Теперь найдем особые точки поверхностей нулевой скорости, не лежащие на оси OX: . В этом случае 2-е уравнение системы [16] можно разделить на y:

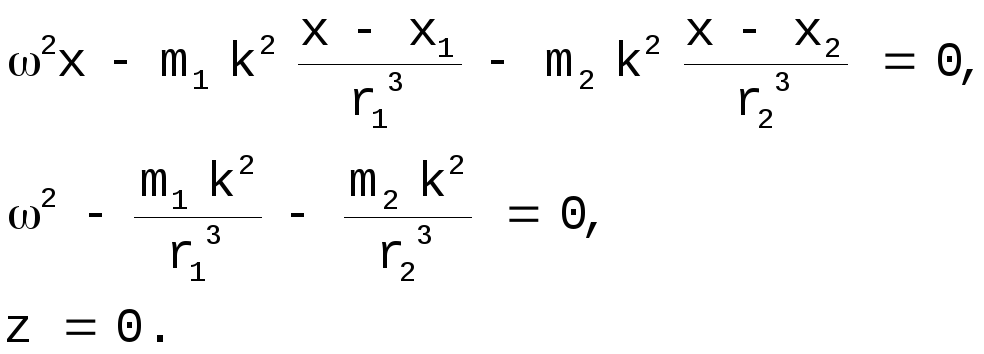[18]

Умножим 2-е уравнение на и вычтем из 1-го:

.

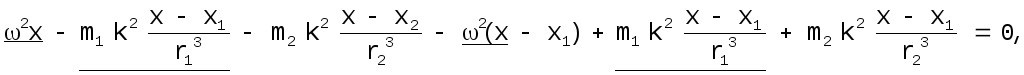
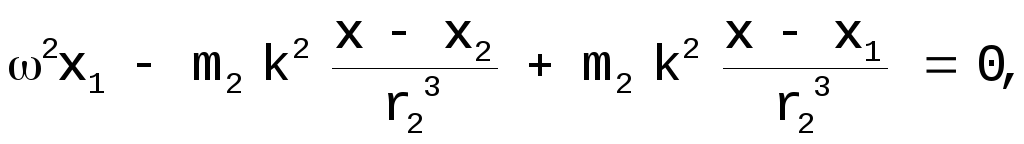
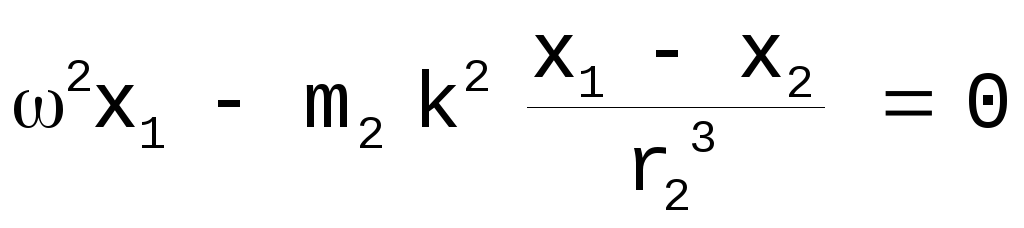Умножим 2-е уравнение на и вычтем из 1-го:

.

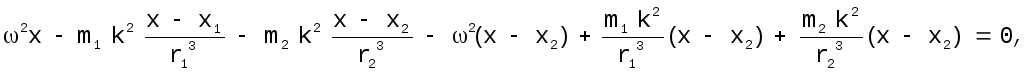
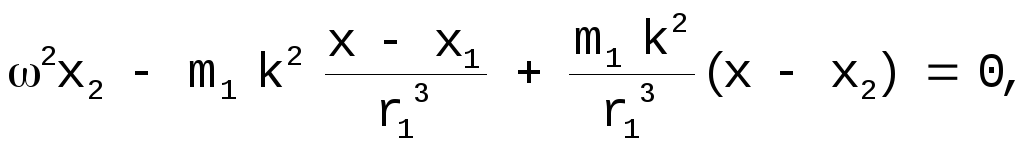
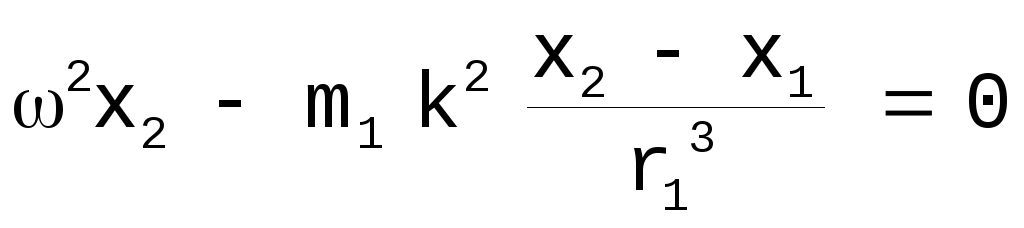Итак

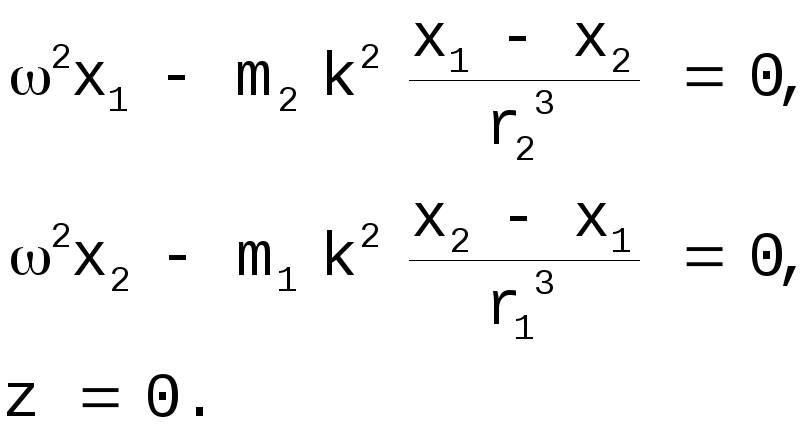[19]

Отметим, что , а . Кроме того, поскольку начало системы отсчета совпадает с центром масс системы тел S и J, то ; .

Разделим 1-е уравнение системы [19] на ;

2-е уравнение системы [19] на . Получим

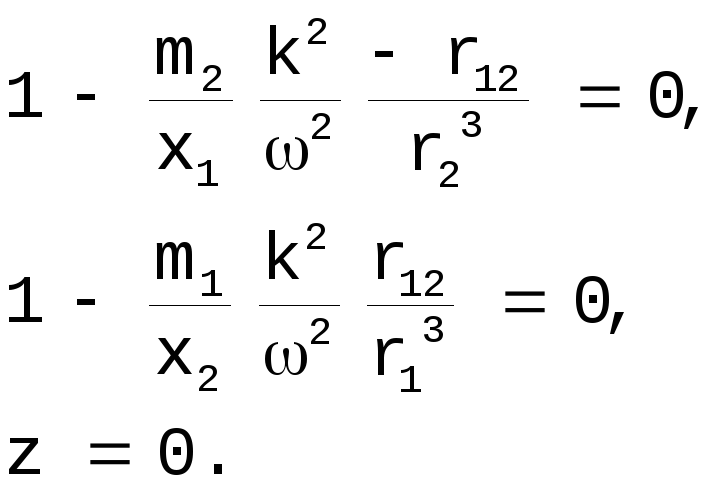Далее

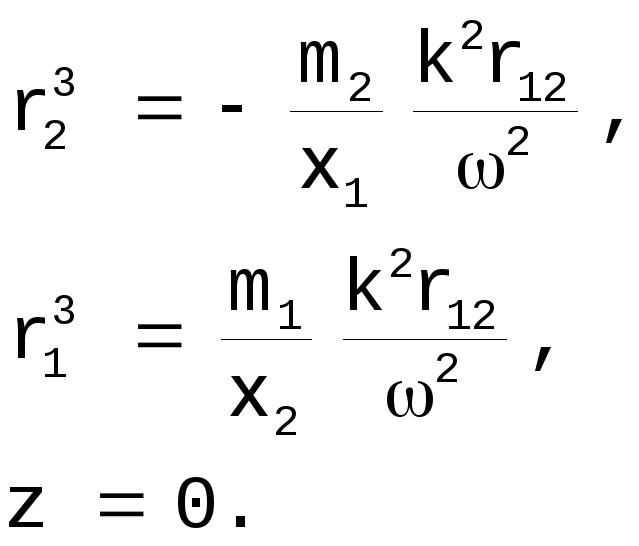
Из последней системы следует

. [20]

Особые точки поверхностей нулевой скорости, не лежащие на оси OX равноудалены от тел S и J. Уточним их положение. Из первого уравнения следует

.

Вспомним [1]: . [1]

Кроме того, выше было получено:

: .

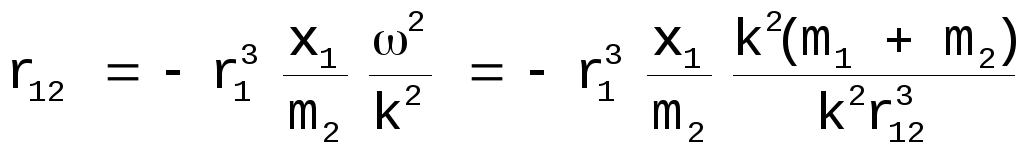Перенесем влево: ,

. Но , подставляя

, итак

, а следовательно [21]

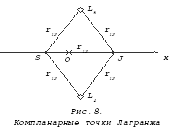
Особые точки образуют равносторонние треугольники с телами S и J независимо от их относительных масс. Это вторая группа решений называется компланарными точками Лагранжа или компланарными точками либрации. Их две. {1} {2} {3}

Таким образом, определено положение всех 5-ти особых точек. {4}

ВОПРОСЫ.

1. Где расположены компланарные точки Лагранжа?

2. Сколько известно компланарных точек Лагранжа?

3. Зависит ли положение компланарных точек Лагранжа от соотношения масс в системе 3-х тел?

4. Сколько всего точек Лагранжа?

Дополнительное рассмотрение: линии Хилла в плоскости орбиты

Вернемся к системе [12], определяющей поверхности Хилла:

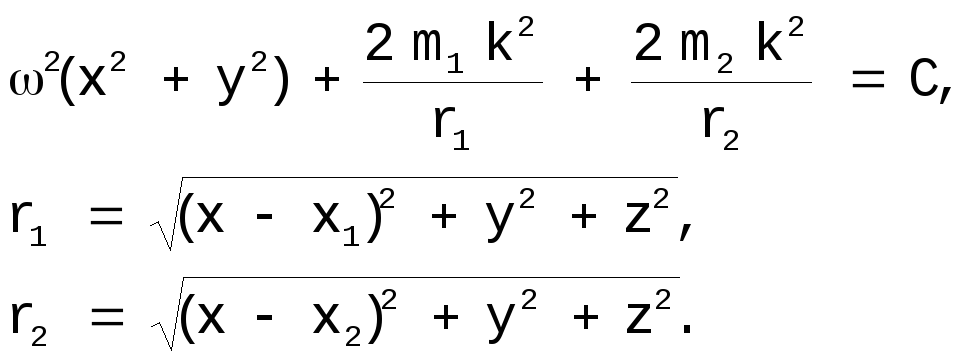
Линии нулевой скорости в плоскости орбиты XOY наиболее интересны, поскольку именно здесь расположены все особенности. Уравнение линий в плоскости XOY:

.

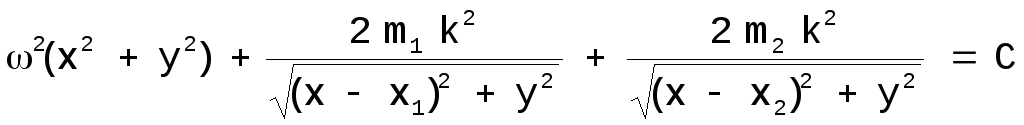Если это уравнение рационализировать и освободить от дробей, то получим многочлен 16-й степени относительно х и у. Если значение одной их переменных взято произвольно, то соответствующее значение другой может быть найдено путем решения этого уравнения численными методами.

Можно избегнуть трудностей численного решения преобразованием уравнения в биполярные координаты, то есть точки кривых могут быть определены расстояниями от двух фиксированных точек {1} – полюсов на оси ОХ. Этот метод неприменим, если кривые не симметричны относительно оси, на которой лежат полюса.

П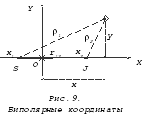усть центры тел S и J совпадают с полюсами; расстояния от этих точек соответственно равны ₁ и ₂. Для перехода в биполярные координаты надо выразить x²+y² через эти величины.

Вспомним [1]. Тогда

. [22]

Заметим следующее -

,

последнее слагаемое равно 0 по выбору начала системы отсчета,

.

Уравнение [22] можно переписать

,

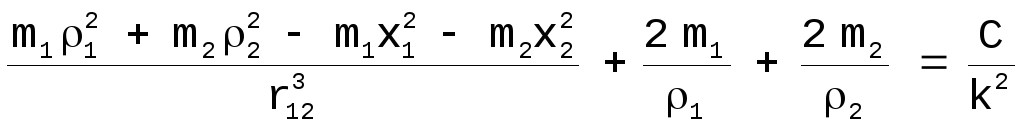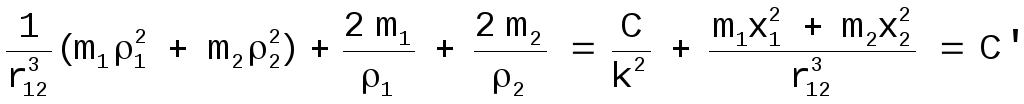[23]

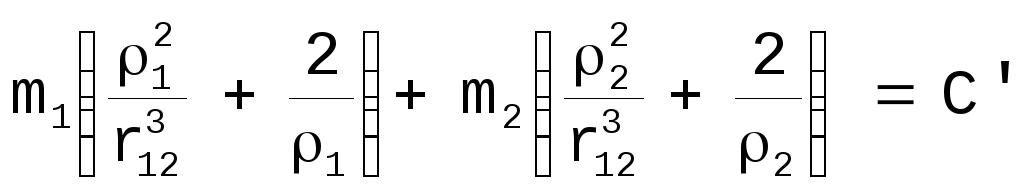. [24]

Если взято произвольное значение ₂, то из этого уравнения может быть вычислено ₁; точками пересечения окружностей с центрами в S и J с соответственно вычисленными значениями радиусов ₁ и ₂ будут точки на линиях нулевой скорости.

Перепишем уравнение [24] в виде (₂ фиксировано!)

,

,

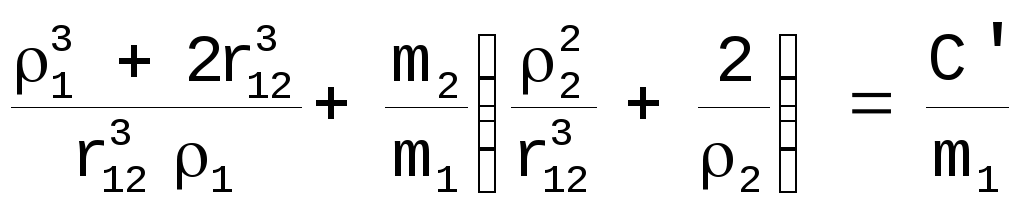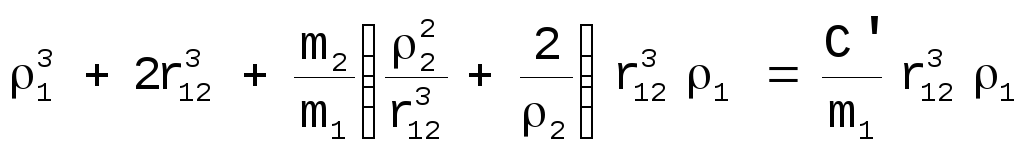, где 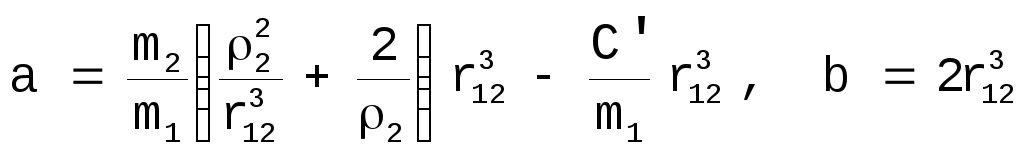. [25]

Так как , то имеется хотя бы один действительный отрицательный корень уравнения [25] при любом значении а. Но ₁ существенно положительная величина, поэтому нас интересуют только положительные решения.

Из уравнения [24] следует, что 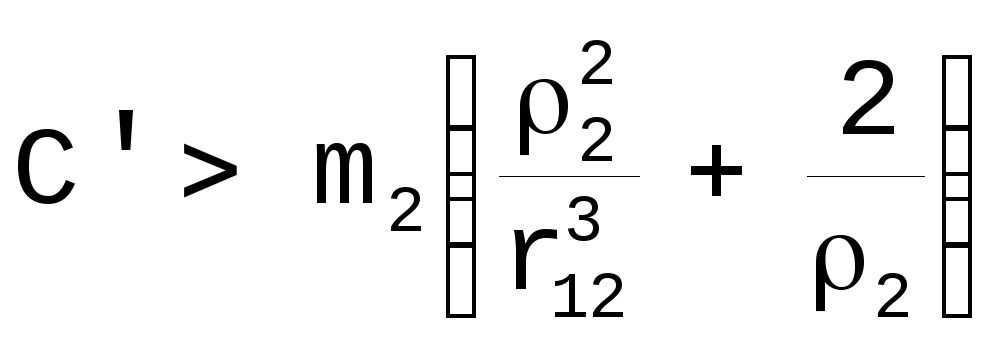при любых ₁ и ₂, а значит коэффициент а<0. В теории алгебраических уравнений доказывается, что кубичное уравнение такой формы имеет три различных действительных корня, если , или

, поскольку всегда а<0, то второй сомножитель положителен. Поэтому неравенство будет выполнено при

. [26]

Предположим, что это неравенство удовлетворено. Тогда корни уравнения [25] можно получить следующим образом:

,

,

, где ₁₁, ₁₂, ₁₃ – три корня кубичного уравнения [25].

Совершенно аналогичное уравнение справедливо, если ₁ фиксировано и вычисляется ₂:

, где

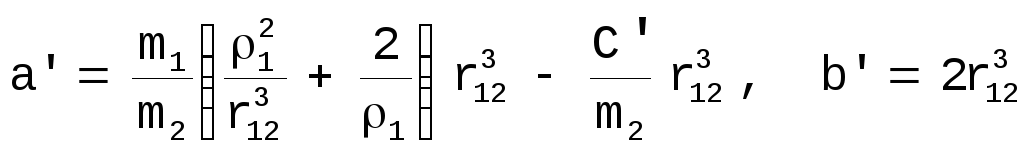
Проведем следующее преобразование

разделим на ₁

.

В предельном случае неравенство, определяющее три действительных корня, переходит в равенство , что позволяет (в пределе!):

разделим на

.

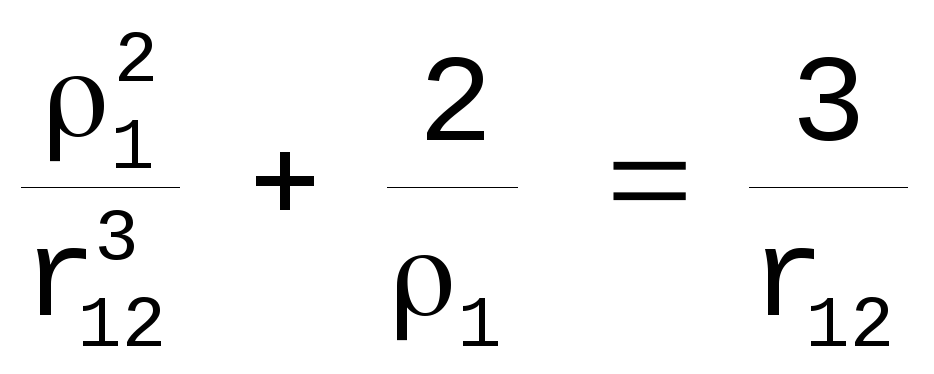Подставим это в первое слагаемое в коэффициенте , получим

.

Поэтому, в пределе () верно

, где . [27]

Решение этого уравнения определяет то крайнее значение ₂, для которого [25] имеет действительные корни.

Условие, при котором уравнение [27] будет иметь действительные корни, аналогично [26] запишется в виде:

;

подставляя вместо его значение и сохраняя только знак равенства, получим

разделим на

,

,

. [28]

Поэтому, чтобы линии нулевой скорости имели действительные точки в плоскости XOY, С’ должно быть больше, в крайнем случае, равно значению, определяемому формулой [28]. Возвращаясь к [23], имеем

, .

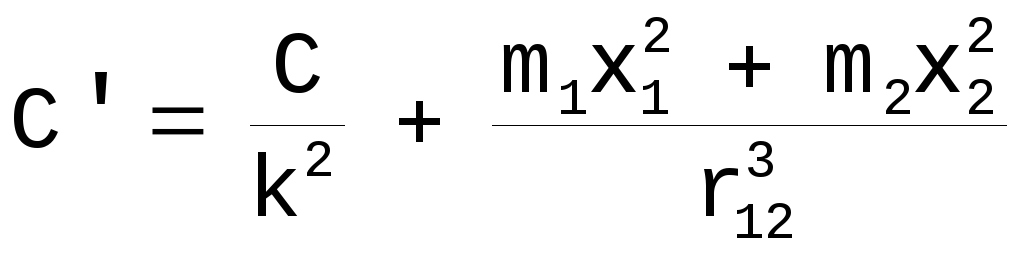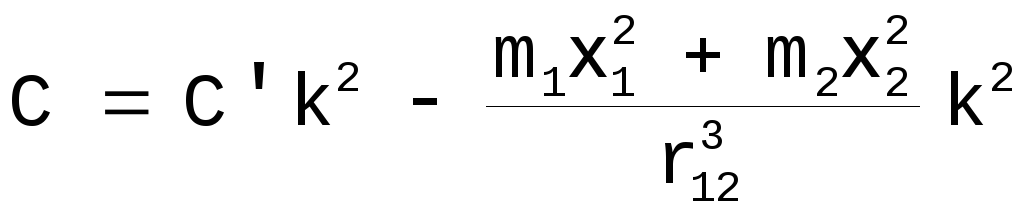Для полученного значения константы Якоби C уравнение [23] примет следующий вид:

,

легко проверить, что данное уравнение выполняется при , то есть поверхности исчезают с плоскости XOY в точках, образующих равносторонние треугольники с массами m₁ и m₂.

Константа Якоби C’, определяемая равенством [28] соответствует поверхности Хилла, проходящей через компланарные точки Лагранжа L₄ и L₅.

ВОПРОСЫ.