Особые точки поверхностей нулевой скорости

Особые точки поверхности определяются, как известно, уравнениями .

Для поверхностей нулевой скорости, уравнение которых имеет вид

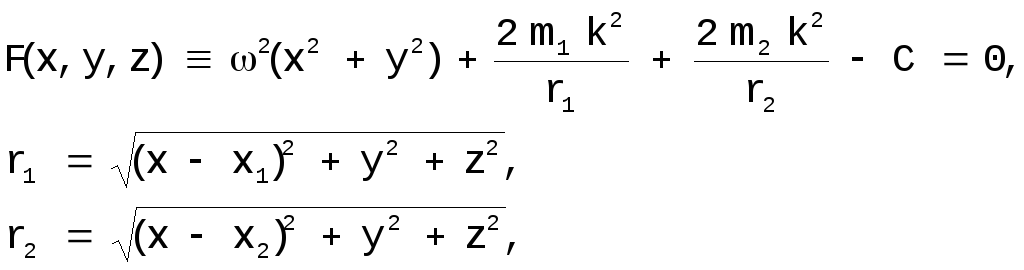[12]

особые точки даются уравнениями

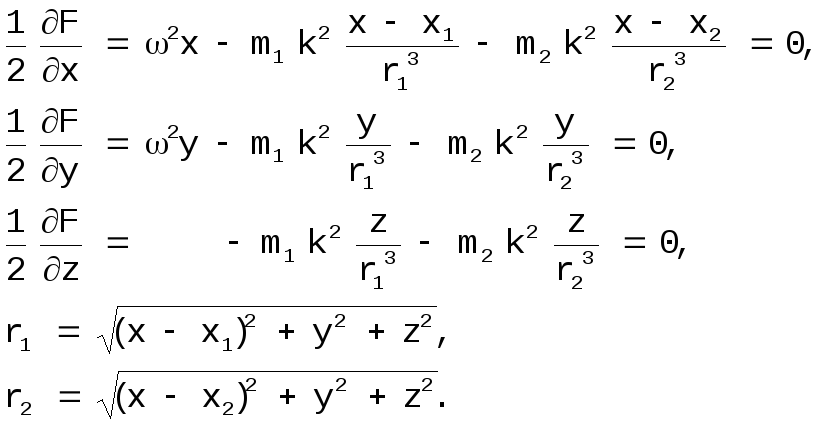[16]

Сравним правые части полученных уравнений с уравнениями движения тела бесконечно малой массы Р [7]:

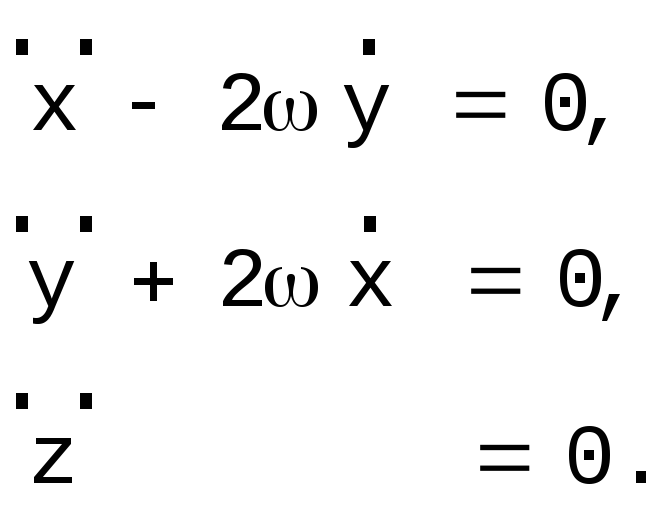
Это уравнения, определяющие положения особых точек поверхностей нулевой скорости. По определению самих этих поверхностей . Поэтому

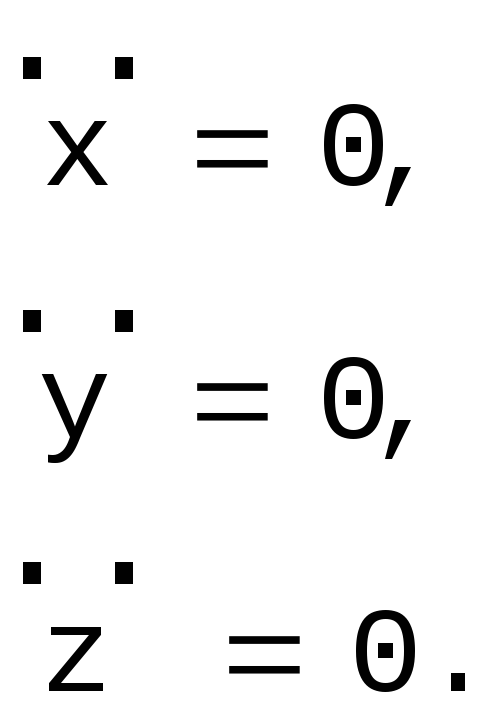
Итак, тело Р, имея соответствующее значение постоянной Якоби и оказавшись в особой точке, будет двигаться с нулевой скоростью и нулевым ускорением! {1} Особые точки поверхности нулевой скорости являются положениями относительного равновесия тела Р; в этих точках тело может находиться в равновесии относительно вращающейся системы координат. {2} Об устойчивости равновесия пока ничего сказано не было.

Кроме того, выражения пропорциональны направляющим косинусам нормали во всех обыкновенных точках поверхности . {Вспомним – уравнение нормали к поверхности : 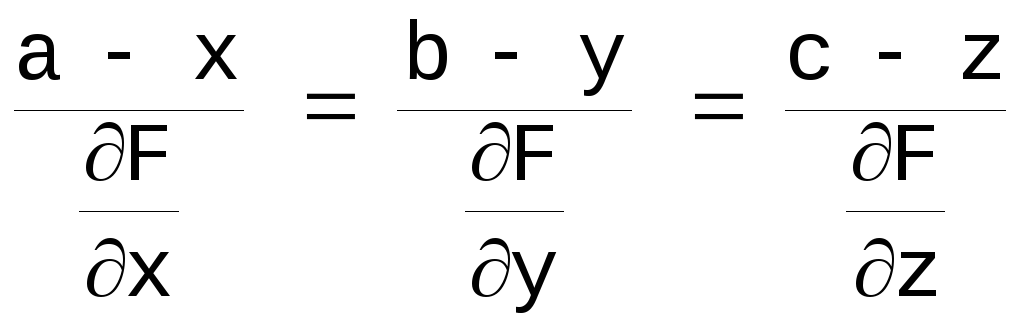, где a,b,c – текущие координаты нормали} Поэтому если бесконечно малое тело Р оказалось на поверхности нулевой скорости, то оно начнет двигаться в направлении нормали. {3} В особых точках положение нормали становится двойным и там тело Р может оставаться в покое относительно вращающейся системы координат.

Особые точки поверхности нулевой скорости называют точками либрации или точками Лагранжа. {4}

Где лежат особые точки? Третье уравнение системы [16] может быть удовлетворено только при z=0. Следовательно, все особые точки лежат в плоскости XOY – плоскости орбиты тел S и J. {5}

ВОПРОСЫ.

1. Как будет двигаться тело Р в особых точках поверхностей нулевой скорости?

2. Являются ли особые точки поверхностей нулевой скорости точками равновесия?

3. Если тело Р находится на поверхности нулевой скорости – как оно будет двигаться в последующие моменты времени?

4. Что такое точки либрации и точки Лагранжа?

5. Где лежат все особые точки?

Коллинеарные точки Лагранжа

Координаты особых точек являются решениями системы 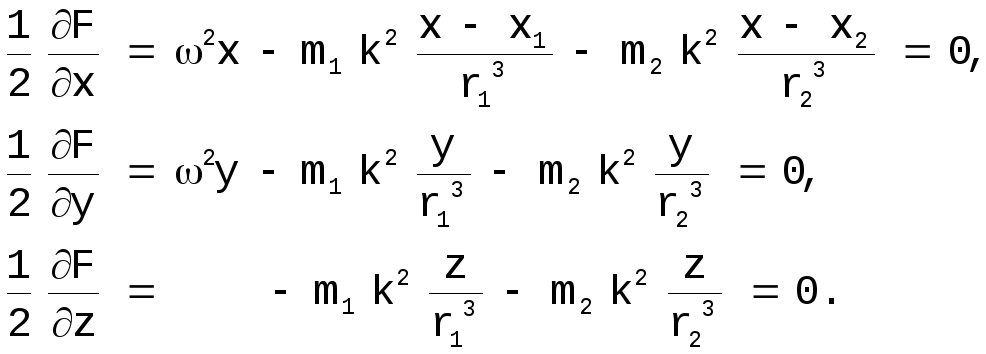[16]:

[16]

Рассмотрим решения, когда . В этом случае искомые особые точки лежат на оси OX и их абсциссы удовлетворяют уравнению

[17]

В знаменателях находятся положительные величины. Пусть  – малая положительная величина. Тогда при и левая часть уравнения ;

при ,

при ,

при ,

при ,

при ,

Функция три раза меняет знак, переходя через ноль:

• один раз между и телом S;

• один раз между телом S и телом J;

• один раз между телом J и .

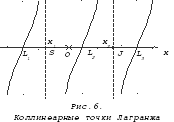
Поэтому на линии, соединяющей центры тел конечной массы S и J, имеется три особых точки. Это первая группа решений называется коллинеарными точками Лагранжа или коллинеарными точками либрации. {1}{2}

Поскольку в уравнение [17], определяющее положение коллинеарных точек, входят массы тел, то их положение существенно зависит от соотношения масс в рассматриваемой системе тел. {3}

ВОПРОСЫ.

1. Где расположены коллинеарные точки Лагранжа?

2. Сколько известно коллинеарных точек Лагранжа?

3. Зависит ли положение коллинеарных точек Лагранжа от соотношения масс в системе 3-х тел?