Интерполирование по таблице функции двух аргументов

Функция задана таблицей своих значений; значениязаданы с шагом, значения- с шагом. Табличные значения функции –, индекс– для, индекс– для,. Требуется найти значение функции для некоторыхи, несовпадающих с узлами таблицы.

Эту задачу можно решить, интерполируя раз попри нескольких табличных значенияходним из методов точечного интерполирования. Так получим таблицу

t1	f=f(xj,t1)
t2	f=f(xj,t2)
…	…
tn	f=f(xj,tn)

Теперь осталось найти значение как было сделано выше.

Пример. Задана функция двух переменных

x t	0.340	0.360	0.380	0.400	0.420	0.440
30	43.380	44.443	45.540	46.671	47.838	49.037
35	49.901	51.038	52.205	53.399	54.620	55.867
40	56.185	57.371	58.580	59.810	61.059	62.326
45	62.238	63.451	64.681	65.925	67.181	68.447
50	68.071	69.294	70.527	71.768	73.015	74.265
55	73.697	74.916	76.138	77.363	78.588	79.813

Найти значение функции

Проинтерполируем 6 раз по столбцам и найдем 6 значений функции для :

x t	0.340	0.360	0.380	0.387	0.400	0.420	0.440
30	43.380	44.443	45.540	45.932	46.671	47.838	49.037
35	49.901	51.038	52.205	52.620	53.399	54.620	55.867
40	56.185	57.371	58.580	59.008	59.810	61.059	62.326
45	62.238	63.451	64.681	65.115	65.925	67.181	68.447
50	68.071	69.294	70.527	70.961	71.768	73.015	74.265
55	73.697	74.916	76.138	76.566	77.363	78.588	79.813

Так получим таблицу

x t	0.387
30	45.932
35	52.620
40	59.008
45	65.115
50	70.961
55	76.566

По этой таблице несложно найти значение функции для :

.

Можно проконтролировать вычисления, изменив порядок интерполирования – вначале найти таблицу , а затем. Результат должен быть тем же.

ДИФФЕРЕНЦИРОВАНИЕ ПО ТАБЛИЦЕ

Интерполяционными формулами как приближением табличной функции можно воспользоваться для приближенного вычисления производной приближаемой функции в произвольной точке. Интерполяционный полином строится обычно для нормированного значения аргумента . Обозначим интерполяционный полином через , а интерполируемую функцию. Тогда

, ,,.

Аналогично .

Найдем производные с использованием формулы Стирлинга. Выпишем ее в виде, предшествующем [14]

.

.

. [18]

В простейшем случае, ограничиваясь первыми слагаемыми, имеем

,

; [19a]

,

. [19b]

Если требуется вычисление производных вблизи начала таблицы, то придется использовать формулу Ньютона для интерполирования «вперед» [16]:

EMBED Equation.3

,

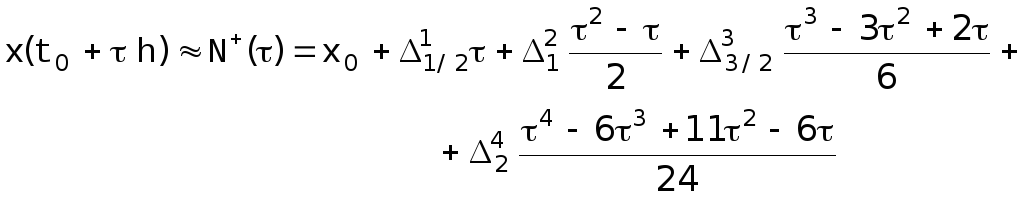
. [20]

Если требуется вычисление производных вблизи конца таблицы, то придется использовать формулу Ньютона для интерполирования «назад» [17]:

,

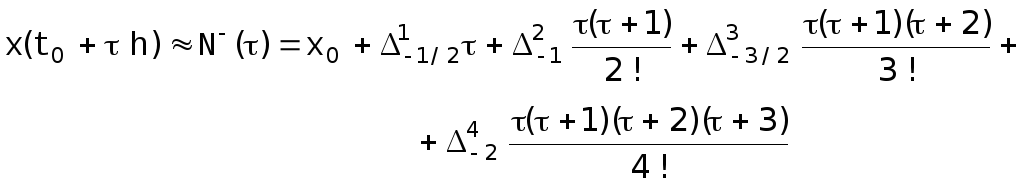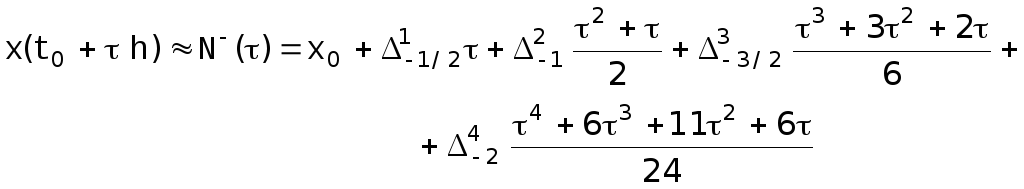
. [21]

Пример. Пусть требуется вычислить значение 1-й 2-й производной x при t=0.05 по формуле Стирлинга.

h=0.1, примем t₀=0, поэтому . Из [12]

, .

,

.

Таким образом, можно находить производные m-го порядка. Очевидно, что порядок искомой производной должен быть не больше порядка используемых разностей. Если порядок производной больше табличных разностей, то она тождественно обращается в 0.

содержание