Метод парабол
Метод
золотого сечения надежный, но медленный.
Если функция
 дифференцируема, то можно построить
гораздо более быстрые методы, основанные
на решении уравнения
дифференцируема, то можно построить
гораздо более быстрые методы, основанные
на решении уравнения .
Корень этого уравнения
.
Корень этого уравнения является точкой минимума, если
является точкой минимума, если ,
и точкой максимума, если
,
и точкой максимума, если .
.
Допустим,
что
 имеет 1-ю и 2-ю производные. Обратимся к
решению уравнения
имеет 1-ю и 2-ю производные. Обратимся к
решению уравнения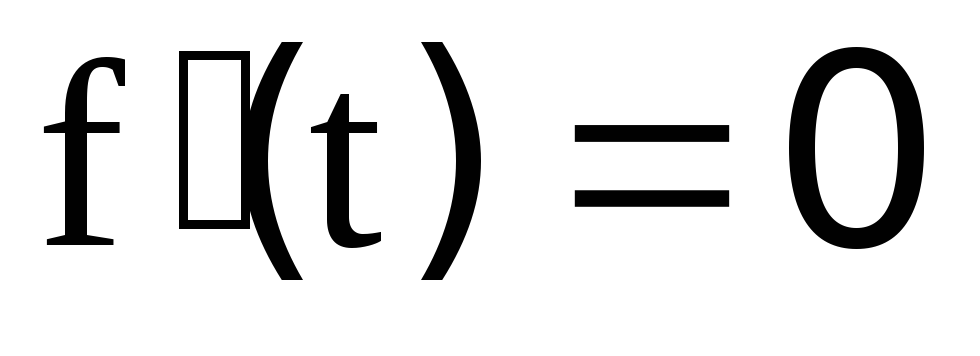 методом Ньютона (см. [24]):
методом Ньютона (см. [24]):
 .
.
Обычно
нулевое приближение можно выбрать
графически. Итерационный процесс,
определяемый этой формулой, сходится
достаточно быстро - квадратично.
Сходимость замедляется если
 ,
тогда сходимость в малой окрестности
экстремума замедляется до линейной.
,
тогда сходимость в малой окрестности
экстремума замедляется до линейной.
На
практике для 1-й и 2-й производных
получаются громоздкие выражения, поэтому
их заменяют конечно-разностными
аппроксимациями [19a]
и [19b]:
 или
или
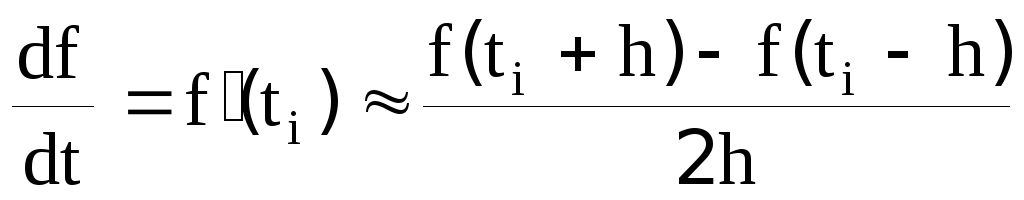 ,
,
 или
или
 .
.
Подставим
это в ньютоновский итерационный процесс:
 . [25]
. [25]
Это
эквивалентно замене кривой на
интерполяционную параболу, построенную
по трем точкам
 .
Обычно выбирают вспомогательный шагh~0.1-0.01
при ручных вычислениях с небольшой
точностью и h~0.01-0.001
при вычислениях с помощью компьютера
(в процессе вычислений длина шага не
изменяется!). Формула [24] наиболее часто
употребляется в вычислениях.
.
Обычно выбирают вспомогательный шагh~0.1-0.01
при ручных вычислениях с небольшой
точностью и h~0.01-0.001
при вычислениях с помощью компьютера
(в процессе вычислений длина шага не
изменяется!). Формула [24] наиболее часто
употребляется в вычислениях.
На
практике рекомендуется в процессе
вычислений проверять сходится ли процесс
к минимуму – 2-я разность (или 2-я
производная) в знаменателе [25] должна
быть положительной. Если она отрицательна,
то итерации сходятся к максимуму, и,
значит, надо сделать достаточно большой
шаг в обратном направлении.
Вычислив
новое приближение, надо проверить,
уменьшилась ли функция
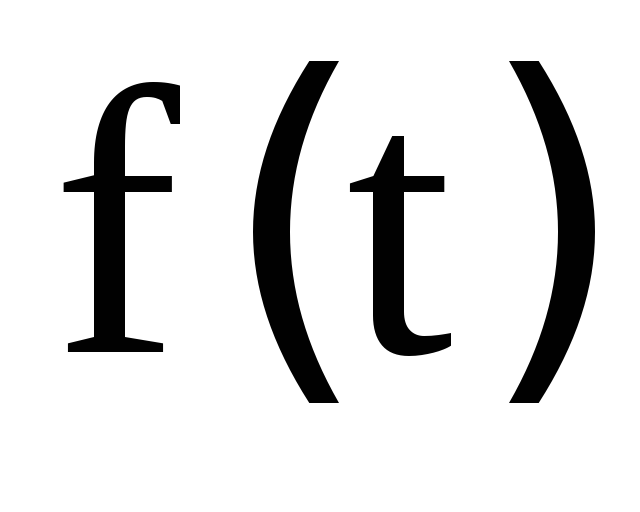 .
Если оказалось, что
.
Если оказалось, что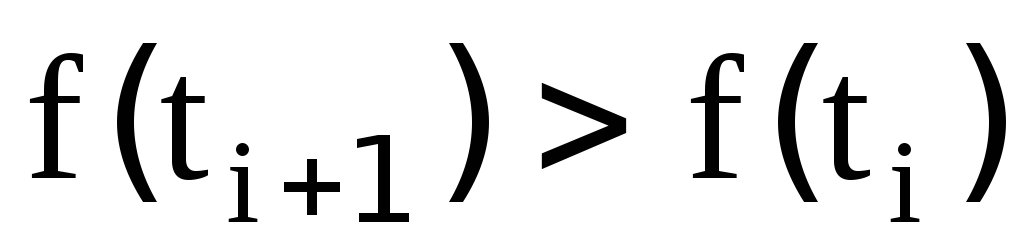 ,
то значение
,
то значение нельзя использовать и надо сделать шаг
в сторону убывания функции
нельзя использовать и надо сделать шаг
в сторону убывания функции .
.
Пример.
Найти минимум функции
 на отрезке [0, 3] с точностью 0.1.
на отрезке [0, 3] с точностью 0.1.
Выберем
t1
=
0.5,
h
=
0.1.
Тогда

 ,
,
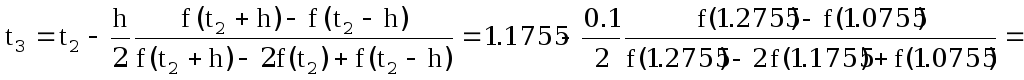
 ,
,

 .
.
Поскольку
 ,
то минимумtmin=1.0
с заданной точностью найден.
,
то минимумtmin=1.0
с заданной точностью найден.
содержание

