
ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
К численному решению уравнений или систем уравнений обращаются если аналитическое решение невозможно или чрезвычайно громоздко. Рассмотрим условия сходимости вычислительного процесса и несколько способов численного решения уравнений.
Пусть задана
непрерывная функция
![]() и требуется найти все корни уравнения
и требуется найти все корни уравнения
![]() . [22]
. [22]
Эта задача распадается на несколько задач: надо
исследовать количество и расположение корней;
найти приближенные значения корней;
вычислить корни с требуемой точностью.
Первую
и вторую задачи можно решать графически
– построить график функции ![]() и найти точки его пересечения с осью
абсцисс. Это очень наглядно. Когда ищутся
только действительные корни, то можно
составить таблицу значений
и найти точки его пересечения с осью
абсцисс. Это очень наглядно. Когда ищутся
только действительные корни, то можно
составить таблицу значений ![]() .
Если в двух соседних узлах таблицы
функция имеет разные знаки, то между
этими узлами лежит нечетное число корней
уравнения [21]. Если эти узлы близки, то,
скорее всего, корень между ними только
один. Четное число корней таким образом
выявить не удастся.
.
Если в двух соседних узлах таблицы
функция имеет разные знаки, то между
этими узлами лежит нечетное число корней
уравнения [21]. Если эти узлы близки, то,
скорее всего, корень между ними только
один. Четное число корней таким образом
выявить не удастся.
Если в уравнениях присутствуют углы и тригонометрические функции, то при вычислениях рекомендовано использовать естественные единицы измерения углов – радианы.
Дихотомия (метод деления пополам)
П усть
найдены такие точкиt0иt1, что
усть
найдены такие точкиt0иt1, что![]() ,
то есть на отрезке [t0,t1]
лежит не менее одного корня уравнения
,
то есть на отрезке [t0,t1]
лежит не менее одного корня уравнения![]() .
.
Найдем середину
отрезка
![]() и вычислим
и вычислим![]() .
Из двух половин отрезка выберем ту, для
которой
.
Из двух половин отрезка выберем ту, для
которой![]() .
Эту половину делим пополам и выбираем
ту половину, на концах которой функция
имеет разные знаки.
.
Эту половину делим пополам и выбираем
ту половину, на концах которой функция
имеет разные знаки.
Е сли
требуется найти корень с точностью,
то продолжаем деление пополам до тех
пор, пока длина отрезка не станет меньше
2.
Тогда середина последнего отрезка даст
значение корня с требуемой точностью.
сли
требуется найти корень с точностью,
то продолжаем деление пополам до тех
пор, пока длина отрезка не станет меньше
2.
Тогда середина последнего отрезка даст
значение корня с требуемой точностью.
Дихотомия проста
и очень надежна: к простому корню она
сходится для любых непрерывных функций
![]() ,
в том числе недифференцируемых. Дихотомия
устойчива к ошибкам округления, скорость
сходимости невелика: за одну итерацию
точность увеличивается примерно вдвое,
то есть уточнение трех цифр требует 10
итераций (210~1000). Но точность
результата гарантируется.
,
в том числе недифференцируемых. Дихотомия
устойчива к ошибкам округления, скорость
сходимости невелика: за одну итерацию
точность увеличивается примерно вдвое,
то есть уточнение трех цифр требует 10
итераций (210~1000). Но точность
результата гарантируется.
Недостатки метода:
Для начала вычислений надо найти отрезок, на котором функция меняет знак;
Если в этом отрезке несколько корней, то неизвестно, к какому из них сойдется процесс;
На системы уравнений дихотомия не обобщается.
Пример.
Решить уравнение![]() с точностью до= 0.1.
с точностью до= 0.1.

Построим график
функции
![]() :
:
Из графика следует, что уравнение имеет единственный корень вблизи t=2. Поэтому выберем отрезок [1.5,2], на концах которого функция меняет знак.
f(t0)<0,f(t1)>0,t0=1.5,t1=2,t2=(1.5+2)/2=1.75
f(t2)=f(1.75)=-0.308<0;
f(t2)<0,f(t1)>0,t2=1.75,t1=2, длина отрезка 0.25,t3=(1.75+2)/2=1.88
f(t3)=f(1.88)=0.019>0;
f(t3)>0,f(t2)<0,t3=1.88,t2=1.75, длина отрезка 0.13,t4=(1.88+1.75)/2=1.82
0.13<2= 0.2, поэтому с требуемой точностью корень уравнения 1.82.
(С точностью до 4-х знаков после точки корень равен 1.8731).
Метод простых итераций
Название
метода происходит от латинского слова
iteratio,
что означает «повторение» (iter
- шаг). Заменим уравнение [22]
![]() эквивалентным ему уравнением
эквивалентным ему уравнением![]() (канонический вид).
(канонический вид).
П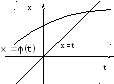 остроим
графики обеих частей уравнения
остроим
графики обеих частей уравнения![]() .
Для левой части это, очевидно, прямаяx
=
t,
являющаяся биссектрисой первого
координатного угла. Для правой части
график есть некоторая линия с уравнением
.
Для левой части это, очевидно, прямаяx
=
t,
являющаяся биссектрисой первого
координатного угла. Для правой части
график есть некоторая линия с уравнением
![]() .
Решением уравнения является абсцисса
точки пересечения этих графиков. Точек
пересечения может быть не одна, а
несколько.
.
Решением уравнения является абсцисса
точки пересечения этих графиков. Точек
пересечения может быть не одна, а
несколько.
Допустим, что каким-либо способом найдено начальное приближение t0. В простейшем методе итераций все дальнейшие приближения строятся по формуле
![]() [23]
[23]
Этот процесс называется простой одношаговой итерацией.
Предположим,
что значение
![]() является точным решением уравнения
[22], тогда погрешности
является точным решением уравнения
[22], тогда погрешности![]() должны быть малыми и по мере итераций
уменьшаться. Найдем зависимость между
должны быть малыми и по мере итераций
уменьшаться. Найдем зависимость между![]() и
и![]() .
Очевидно
.
Очевидно
![]() ,
,
![]() ,
подставим это в [23], получим
,
подставим это в [23], получим
![]()
![]()
учитывая
![]() и пренебрегая высшими производными,
и пренебрегая высшими производными,
![]() .
.
Итак,
если
![]() ,
то
,
то![]() и приближение
и приближение![]() будет отстоять от точного решения
будет отстоять от точного решения![]() дальше, чем
дальше, чем![]() .
В этом случае нет сходимости
последовательности
.
В этом случае нет сходимости
последовательности![]() к
к![]() .
.
если
![]() ,
то
,
то![]() и можно ожидать, что последовательность
и можно ожидать, что последовательность![]() ,
если
,
если![]() выбрано достаточно близким к
выбрано достаточно близким к![]() ,
будет сходиться к
,
будет сходиться к![]() .
Причем, при
.
Причем, при![]()
![]() и
и![]() будут иметь одинаковые знаки и сходимость
будут иметь одинаковые знаки и сходимость![]() к
к![]() будет монотонной; при
будет монотонной; при![]()
![]() и
и![]() будут иметь разные знаки и
будут иметь разные знаки и![]() сходится к
сходится к![]() ,
колеблясь около
,
колеблясь около![]() .
.
случай
![]() требует специального рассмотрения.
требует специального рассмотрения.

![]() -
точное решение;
-
точное решение;
![]() -
приближенное решение.
-
приближенное решение.
Пример. В небесной механике часто приходится решать уравнение Кеплера вида
![]() ,
где t
– угол.
,
где t
– угол.
![]() ,
,
![]() ,
,
![]() -
итерационный процесс сходится,
-
итерационный процесс сходится,
в
качестве приближенного решения возьмем
![]() ,
,
![]()
![]()
![]()
![]()
Итак,
решение
![]() =1.1104.
=1.1104.
Система 2-х уравнений с двумя неизвестными
![]()

![]()
предположим, что эту систему можно представить в виде
![]()

![]()
процесс итераций сходится только в случае, если
![]()

![]()
Приближенное
решение
![]() можно найти графически как координаты
точки пересечения графиков функций
можно найти графически как координаты
точки пересечения графиков функций![]() и
и![]() .
Тогда
.
Тогда
![]()
![]()
![]()
![]() и
т.д.
и
т.д.
П ример.
Дана система уравнений
ример.
Дана система уравнений ![]()
![]()
Найти решение.
![]()

![]()

![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Проверим
![]() и
и
![]() ,
решение должно сходиться, за исключением
точек, где
,
решение должно сходиться, за исключением
точек, где
![]() и
и![]() ,
это сомнительные точки.
,
это сомнительные точки.
В качестве нулевого приближения выберем решение
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
