§ 54. Механическая аналогия.

Остановимся теперь на одной простой механической схеме с целью лучшего уяснения принципа замкнутости тока, а также для того, чтобы наглядно показать значение введенного Максвеллом в науку представления об электрическом смещении как об упругой деформации.

Рассмотрим некоторый цилиндр К (рис. 110) с поршнем Р, периодически двигающимся вперед и назад благодаря соответству­ющему механическому устройству. При посредстве труб T₁ и Т₂ цилиндр этот соединяется с двумя резервуарами, М и N, как пока­зано на рисунке. Допустим теперь, что цилиндр, соединительные трубы и нижние части резервуаров наполнены ка­кой-нибудь жидкостью, на­пример, водою; остаю­щиеся же части резер­вуаров заполнены возду­хом. Очевидно, что в за­висимости от направления движения поршня Р в ци­линдре К в жидкости, за­полняющей цилиндр, будут возникать известные дав­ления, совокупность кото­рых мы можем, аналогии ради, назвать „вододвижущей силой", так как они действительно являются непосредственной причиной, приводящей в движение воду в нашей системе. Именно, периодические движения поршня будут сопровождаться соответствующими токами жидкости в тру­бах Т₁ и Т₂, причем в резервуарах М и N уровни жидкости будут то повышаться, то понижаться, в зависимости от направления тока жидкости в трубах. Ясно, конечно, что в данном случае, если только мы можем пренебречь сжимаемостью жидкости и дефор­мированием всех стенок нашей системы, резервуаров и труб, в резервуар М будет прибывать столько же жидкости, сколько ее уйдет из резервуара N, и наоборот. В данном случае нет замкну­того контура, по которому происходит движение вещества, так как резервуары М и. N изолированы друг от друга.

Совершенно таким же представляется нам и ток электрический, если мы будем игнорировать процессы в диэлектрике, а все свое внимание сосредоточим только на проводниках. Но благодаря Фарадею и Максвеллу мы знаем теперь, что такая точка зре­ния была бы неправильна. Электрический ток может течь и через

181

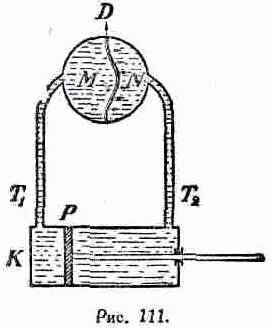
диэлектрики, но только не непрерывно в одном направлении, ибо упругие реакции в диэлектрике в конце концов кладут предел той деформации электрического смещения, процесс возникновения или вообще изменения которой и составляют, по Максвеллу, ток в диэлектрике. Не трудно, однако, рассмотренную выше модель изменить так, чтобы она иллюстрировала все то, что нами говори­лось о замкнутости тока в цепи с конденсатором. Возьмем опять прежний цилиндр К. с поршнем Р, приводимым в попеременное движение при помощи соответствующего меха­низма. В данном случае пусть трубы T₁ и T₂ соединяют цилиндр, как показано на рис. 111, с двумя диаметрально противоположными сто­ронами одного общего резервуара, внутри ко­торого находится сплошная упругая перего­родка D, состоящая, например, из резиновой пластины и делящая весь объем резервуара на две части, М и N. Допустим далее, что у весь объем рассматриваемой системы, т. е. цилиндр, соединительные трубы и ка­меры М и N, сплошь заполнены жид­костью, скажем, водой. В отличие от предыдущего случая, камеры М и N не изолированы теперь одна от дру­гой. Действительно, всякое увеличение количества воды в камере М вызовет упругую деформацию перегородки D, которая будет изгибаться и при этом вытеснит соответствующее количество воды из камеры N. При каждом данном значении разности давлений в камерах М и N степень деформирования упругой перегородки D будет совершенно определен­ная и притом такая, что упругая реакция со стороны перегородки будет уравновешивать разность давлений с обеих ее сторон. Если эта разность давлений перестанет существовать, упруго деформирован­ная перегородка немедленно вернется в свое нормальное положение, ее вынужденное состояние прекратится. При переменном движении поршня, т. е. при возникновении в рассматриваемой системе пере­менной „вододвижущей силы", перегородка D будет периодически изгибаться то в ту, то в другую сторону, соответственно напра­влению тока жидкости и вообще материи в той замкнутой цепи, которую в настоящем случае представляет наша система. Таким образом, модель, изображенная на рисунке 111, схематически иллю­стрирует замыкание электрического тока через диэлектрик.