1) Pinch — по-английски означает „ущемление".

§ 115. Величина и направление силы электромагнитного взаимо­действия двух контуров с током.

Рассмотрим теперь случай двух контуров, по которым проте­кают токи i₁ и i₂. Электрокинетическая анергия такой системы определяется выражением:

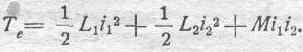
Допустим, что х есть геометрическая координата, от которой зависит форма и взаимное расположение контуров. Электромагнит­ная сила, стремящаяся изменить х, будет:

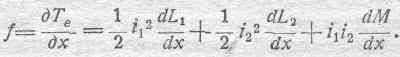
394

Если движение системы, соответствующее изменению переменной х таково, что каждый из контуров движется, как твердое тело, то l₁ и L₂ будут независимы от х, к выражение для электромаг­нитной силы, могущей изменить координату X, приведется к форме:

Выражение (125) дает возможность непосредственно определить величину и направление электромагнитной силы взаимодействия двух контуров: направление силы соответствует такому направле­нию движения, в котором поток взаимной индукции Mi₁ или Mi₂ увеличивается. Действительно, если токи одного направления (см. рис. 165), то будем иметь:

Если далее, х есть расстояние между контурами, то можем написать:

так как при увеличении расстояния между контурами коэффициент взаимной индукции М уменьшается. Следовательно, в случае токов одинаково направленных:

т. е. сила направлена в отрицательную сторону, именно в сторону уменьшения взятой нами координаты — расстояния между контурами. Стало быть, контуры в этом случае сближаются, и поток взаимной индукции возрастает. Все это соответствует рассмотренной выше физической картине явления: магнитные линии, общие для обоих контуров, сокращаются и сближают контуры.

Если же токи в контурах противоположного направления (см. рис. 166), то произведению i₁i₂ мы должны приписать знак минус:

Следовательно, и направление силы в этом случае будет обратное предыдущему случаю:

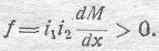
Таким образом, в случае противоположно направленных токов, сила взаимодействия направлена в сторону увеличения координаты х, т. е. в этом случае будет иметь место взаимное отталкивание контуров, сопровождаемое опять же „увеличением" потока взаимной индукции (увеличение здесь надо понимать как уменьшение по абсолютной величине потока, отрицательного по знаку). Физическую природу отталкивания уясняет рисунок 166. Потоки обоих контуров,

395

в промежутке между проводами оказываются в этом случае одного направления. В силу бокового распора магнитных линий, контуры стремятся удалиться один от другого.

Что касается работы электромагнитной силы, то принимая во внимание соотношения:

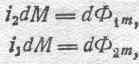
для элементарной работы имеем:

При этом в обоих случаях будет:

dA>0, так как для случая притяжения:

а для случая отталкивания:

§ 116. Случай электромагнитного взаимодействия любого числа

контуров с током.

Обратимся к общему случаю системы, состоящей из произволь­ного числа контуров. Электрокинетическая энергия системы равна:

Будем изучать силу, действующую, например, на первый контур, вследствие присутствия всех остальных. Тогда внешняя электро­магнитная сила, действующая на первый контур в избранном напра­влении 0X, т. е. составляющая результирующей силы взаимодей­ствия между первым контуром и всеми остальными, определится выражением:

В зависимости от выбора того или иного направления за ось координат, получим ту или иную составляющую электромагнитной силы. Наибольшее возможное значение этой составляющей мы получим, если за ось x-ов изберем направление равнодействующей. В этом случае выражение (126) определит собою полную величину электромагнитной силы.

Так как величина:

396

есть не что иное, как поток взаимной индукции, сцепляющийся с первым контуром и создаваемый всеми остальными контурами (Ф_1m), то можем написать:

Совершенно ясно, что физическая картина явления не зависит от того, каково происхождение потока Ф_1m. Таким образом, фор­мула 127 пригодна и в том случае, когда поток Ф_1m есть, например, поток постоянного магнита, т. е. она дает, как было уже указано, наиболее общее выражение для внешней электромагнитной силы, действующей на данный проводник. Элементарная работа электро­магнитной силы в этом случае выражается вполне аналогично преды­дущим случаям:

т. е. она равна произведению силы тока в первом контуре на при­ращение охватываемого им внешнего потока, т. е. потока взаимной индукции.

Мы рассматривали электромагнитную силу, действующую на первый контур. Совершенно очевидно, что выражения для сил, приложенных к любому другому контуру системы, будут вполне анало­гичны.