§ 103. Общие выражения для магнитных потоков, сцепляю­щихся с отдельными контурами системы.

Рассмотрим теперь самый общий случай системы из n электри­ческих цепей. В этом случае, т. е. при наличии любого числа отдельных цепей, мы имеем:

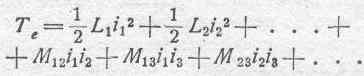
Составим для этих цепей выражения р=дT_e/дi^:

Эти выражения представляют собою, с точки зрения высшей механики, моменты количества движения в электрокинетическом процессе, связанном с каждою отдельною цепью. В то же время на основании изложенного в предыдущих параграфах ясно, что мы можем написать:

p₁=Ф₁

p₂=Ф₂

p₃=Ф₃

. . . . ,

………,

т. е. величины р по существу являются не чем иным, как полными магнитными потоками, сцепляющимися с каждою из n цепей. Таким образом, останавливая наше внимание, например, на первой цепи, получаем:

' Мы видим, что полный магнитный поток, сцепляющийся с неко­торою цепью, состоит из двух частей, имеющих характерные особенности. Первая часть есть полный поток самоиндукции, сцепляющийся с данною цепью:

Ф_1s=L₁i₁.

Вторая часть представляет собою сумму отдельных потоков взаимной индукции, сцепляющихся с тою же цепью и обусловли­ваемых наличием токов i₂, i₃ и т. д.:

где k принимает всевозможные (n-1) значения, кроме 1.

360

Итак, полный магнитный поток, сцепляющийся с первою цепью, можем представить так:

Аналогично можем написать для других цепей:

причем во всех этих выражениях значок k принимает всевозможные (л — 1) значения, кроме того, которое стоит в качестве значка при коэффициенте самоиндукции.

§ 104. Общие выражения для электродвижущих сил, индукти­руемых в отдельных цепях системы.

На основании всего вышеизложенного мы можем, подводя итоги, написать ряд нижеследующих соотношений для электродвижущих сил, индуктируемых в отдельных цепях рассматриваемой системы:

или, что то же:

или

или затем:

361

или далее:

или же, наконец:

где

Таким образом, полная электродвижущая сила, индуктируемая в каждой из цепей рассматриваемой системы, вообще говоря, состоит из двух слагаемых. Первое есть электродвижущая сила самоиндукции, могущая возникать в некоторой цепи вследствие изменений электромагнитного процесса в этой цепи, рассматриваемой совершенно самостоятельно, вне какой-либо связи с другими цепями той же системы. Второе слагаемое есть результирующая электродвижущая сила взаимной индукции, которую необходимо рассматривать как сумму отдельных электродвижущих сил, возникающих в данной цепи вследствие изменения электромагнитных соотношений, связывающих эту цепь с другими частями системы, т. е. вследствие изменения отдельных потоков взаимной индукции, сцепляющихся с данной цепью.

§ 105. Роль короткозамкнутой вторичной цепи.

При рассмотрении явлений самоиндукции и взаимной индукции мы видели, что величина полной ЭДС, возникающей в некотором проводящем контуре в качестве реакции на производимое изменение общих электромагнитных условий, зависит не только от обстоя-

362

тельств, характеризующих данную цепь, но и от присутствия других цепей, не связанных электрически с данной:

где Ф_s есть поток самоиндукции данного контура, а Ф_m —поток взаимной индукции, т. е. поток, обязанный своим существованием какому-нибудь внешнему для данного контура току (или токам). Чтобы лучше уяснить себе это влияние посторонних цепей, рассмотрим простейший случай двух цепей (рис. 161).

Пусть L₁ и L₂ — их коэффициенты самоиндукции, r₁ и r₂ — омические сопротивления, М-—коэффициент взаимной индукции. В одной из них (в первой) действует некоторая внешняя электродви­жущая e₁ в другой никакой внешней ЭДС нет. Для простоты возьмем случай, когда:

L₁=const,

L₂=const,

М=const.

Составим уравнение для тока в пер­вой цепи. Сила тока i₁ в каждый дан­ный момент равна, согласно закону Ома, сумме действующих в контуре ЭДС, де­ленной на сопротивление, т. е.

или

т. е. внешняя ЭДС преодолевает омическое сопротивление, обрат­ную ЭДС самоиндукции и ЭДС взаимоиндукции.

Для второго контура, в котором нет никакой внешней ЭДС, имеем аналогичное соотношение:

Исключим из уравнения (111) производную di₂/dt Для этого опре­делим ее величину из

Подставляя в (111), получаем:

363

Сделаем еще одно допущение. Именно, положим, что:

r₂=0,

т. е. представим себе, что во второй цепи мы имеем дело со сверх­проводником. Это в значительной степени упрощает окончательный вывод и позволяет легче разобраться в физическом смысле полу­ченного соотношения, характеризующего общие электромагнитные ' условия. Тогда из последнего уравнения получаем:

или, вводя обозначение:

имеем:

Итак, выражение для тока в первой цепи при наличии второй цепи, электромагнитно связанной с первой, мы привели к такому виду, какой мы получили бы, если бы второй цепи совсем не было, а первая обладала коэффициентом самоиндукции:

Таким образом, величину L'₁ мы можем рассматривать в каче­стве некоторого действующего коэффициента самоиндукции пер­вичной цепи, пользуясь которым мы как бы игнорируем наличие вторичной цепи и ведем расчет так, как будто бы существует только одна первичная цепь сама по себе. При этом, на основании данного выше соотношения М (L₁L₂), ясно, что, в зависимости от величины коэффициента связи k, будем иметь то или иное значение L'₁.

Если коэффициент связи k равен единице, т. е. М=(L₁L₂), то получаем идеальный случай:

L'₁=0,

другими словами, электромагнитная инерция рассматриваемой (пер­вой) цепи как бы совершенно уничтожается действием коротко замкнутой вторичной сверхпроводящей цепи.

Если коэффициент связи k равен нулю, т. е. M=0, то имеем:

l'₁=l_i,

другими словами, в этом случае присутствие вторичной цепи не оказывает никакого влияния на электромагнитный процесс, про­исходящий в первичной цепи.

364

При всех значениях коэффициента связи, больших нуля и меньших единицы, значение действующего коэффициента самоиндукции L'₁ будет больше нуля и меньше L₁, т. е.:

0<l'₁<l_i.

Таким образом, хотя истинный коэффициент самоиндукции ка­ждого контура и является функцией только его геометрических раз­меров, но в случае системы из нескольких электромагнитно свя­занных между собою контуров, каждый из них ведет себя по отношению к внешней ЭДС как контур, обладающий коэффициен­том самоиндукции L', величина которого для простейшего случая двух цепей определяется данным выше соотношением и может быть изменена путем изменения коэффициента связи k. Это именно и позволяет нам назвать величину:

действующим (эквивалентным, эффективным) коэффициентом само­индукции.

Если r₂0, сущность явления не меняется, лишь математическое его выражение получается сложнее.

Обратимся к физическому смыслу рассмотренного явления, т. е. кажущегося уменьшения коэффициента самоиндукции контура вследствие присутствия вблизи него другого замкнутого проводящего контура. Дело в том, что возникновение в первом контуре тока i₁ под действием приложенной к нему внешней электродвижущей силы е₁ вызывает возникновение во втором контуре тока i₂, вообще говоря, обратного направления, так как магнитный поток Ф₁, на­растающий вокруг первого контура, пересекает второй контур. Вторичному току i₂ соответствует вторичный поток Ф_II, направле­ние которого обратно направлению потока Ф_I. Таким образом, по­ток Ф_II полностью или частично (в зависимости от степени связи) компенсирует действие потока Ф_I. В результате, реально суще­ствующий поток, сцепленный с первым контуром, оказывается меньше, чем при отсутствии вторичного контура. Следовательно, меньше будет и обратная ЭДС, индуктируемая в первом контуре, т. е. этот контур будет оказывать меньшее противодействие уста­новлению в нем тока. Иными словами, электромагнитная инерция контура становится меньше.

Все изложенное относится к категории явлений, охватываемых обобщенным законом Ленца, о котором мы уже говорили в главе I (см. § 29). Закон этот гласит, что всякая электромагнитная система стремится сохранить неизменным связанный с ней магнитный поток (количество движения). Именно такое стремление обнаруживается и в данном случае: на установление внешним воздействием (внеш­ней ЭДС) потока в первом контуре система реагирует созданием обратно направленного магнитного потока, обусловленного наличием второго проводящего контура.

365