§ 50. Теорема Максвелла.

Представим себе замкнутую поверхность s, внутри которой как-либо распределены электрические заряды q₁,q₂, q₃ и т. д. Пусть ds представляет собою элемент этой поверхности (рис. 106).

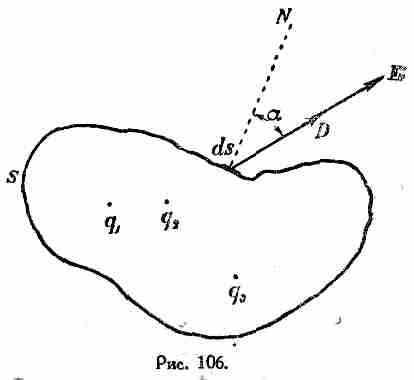
Обозна­чим через  угол, образуемый внешнею нормалью N к этому эле­менту поверхности и направлением электрической силы (напряжения поля) E в той точке, где находится рассматриваемый элемент по­верхности.

Если диэлектрическая постоянная среды есть  и если при этом  постоянно для всех точек среды, то по теореме Гаусса, выве-

174

денной в § 2 для магнитного поля и формально распространяемой также на электрическое поле, имеем:

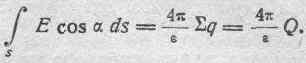
Разделив обе части этого равенства на 4/ и внеся постоянный множитель /4 под знак интеграла, получим:

Выражение E/4 должно

иметь размерность коли­чества электричества на единицу поверхности. Максвелл положил

D=E/4, (30)

на основании чего полу­чается крайне простая по форма и весьма важная по содержанию зависимость:

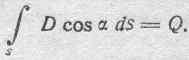
В этом выражении величина Dcosds есть поток электриче­ского смещения сквозь элемент поверхности ds, a Dcos — нор­мальная составляющая электрического смещения сквозь этот эле­мент поверхности.

Для неоднородных и анизотропных диэлектриков, у которых  не постоянно, мы не умеем доказать аналитически справедливость соотношения (31), но Максвелл ввел гипотезу, согласно которой оно справедливо для любых диэлектриков, независимо от их физи­ческих свойств. Все следствия, которые были выводимы из этого допущения, оправдывались при опытной проверке, и, таким образом, они в полной мере подтверждают справедливость высказанной Максвеллом гипотезы. До сих пор неизвестно ни одного факта, находящегося с ней в каком-либо противоречии.

Таким образом, мы будем считать справедливым в самом общем случае соотношение (31):

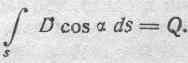
Понимая его в этом обобщенном смысле, мы будем называть его теоремой Максвелла. Итак, теорема Максвелла гласит: полное

175

электрическое смещение сквозь любую замкнутую поверхность в направлении изнутри наружу равно полному количеству электри­чества, находящегося внутри этой замкнутой поверхности.

§ 51. Природа электрического смещения.

Максвелл в своих рассуждениях относительно электрического смещения совершенно не касается природы электричества и того, как надо понимать его движение. Все это не имеет значения в фор­мальных построениях и не отражается на данных выше соотно­шениях.

Если, например, мы имеем два проводника А и В с зарядами +q и -q (рис. 107), то при соединении их посредством проводника С произойдет нейтрализация зарядов, и мы не будем в состоянии обнаружить в какой-либо части системы присутствия электричества того или иного знака.

При формальном рассмотрении вопроса для нас важно лишь то, что произошло движение электри­чества, приведшее к нейтрализации, а не способ и порядок, в котором протекало явление; например, двигалось ли по проводнику только коли­чество электричества +q от А к В, или, наоборот, -q от В к А, или заряды двигались друг другу навстречу.

Современная наука дает некоторые указания касательно электри­ческого строения материи, однако, этого еще далеко недостаточно для построения полной картины электрических явлений в целом, Можно предполагать, и для этого есть основание, что всякое веще­ство, вообще, представляет собою в своем нормальном состоянии некоторую совокупность элементарных электрических зарядов раз­ных знаков, взаимно нейтрализующихся в отношении своих внешних электрических действий, подобно тому, как не оказывает внешних электрических действий некоторый объем электролита, содержащий равные количества ионов разных знаков. Одним словом, всякое вещество мы должны представлять себе как пространство, запол­ненное двумя равномерными распределениями элементарных эле­ктрических зарядов противоположных знаков, при чем в так назы­ваемых диэлектриках эти две системы зарядов упруго связаны одна с другой. Под влиянием внешнего воздействия, внешнего электрического поля, происходит смещение этих двух электрических распределений. Одно из них, положительное, смещается в напра­влении поля; другое, отрицательное, смещается в противоположном направлении. Этот процесс мы можем рассматривать как возникно­вение упругой деформации в среде, ибо рассматриваемые смещения происходят за счет преодоления внешними силами указанных выше упругих связей между двумя электрическими распределениями. Ясно, конечно, что при прекращении внешних воздействий проис­ходят обратные движения элементарных зарядов благодаря упругим связям, и среда возвращается в нормальное, недеформированное

176

состояние. Так можно понимать механизм электрического смещения в диэлектрике. При этом, повторяем, с формальной стороны не важно, какое именно электричество, положительное или отрица­тельное, приходит в движение и в какой степени они участвуют в этом движении. Важно лишь то, что они вынуждаются к сдвижению друг относительно друга. Поэтому, ради простоты; мы можем в наших рассуждениях принимать, что движется только одно поло­жительное электричество. В действительности же, быть может, происходит как раз обратное.

Что касается того, что, с физической точки зрения представляет собою так называемая „пустота" и какова ее электрическая при­рода, т. е. каким именно образом можно, хотя бы совершенно пред­положительно, представлять себе механизм деформации электри­ческого смещения в пустоте, то по этому поводу физика пока еще не дает никакого определенного ответа. Приходится поэтому при­нять как факт, что электрическое поле и электрическое смещение могут иметь место и в „пустоте". Они могут в пустоте и возни­кать, и ослабевать. Следовательно, и в пустоте могут быть токи смещения. Из всего этого необходимо только заключить, что тер­мин ,,пустота" следует понимать как чисто условное обозначение пространства, в котором нет обычной материи, но в котором все же могут происходить физические явления и которое может быть местом распределения энергии. Представление о мировом эфире, заполняющем все физическое пространство и наделенном извест­ными свойствами, есть результат одной из попыток человеческой мысли проникнуть в природу „физической пустоты". Некоторые современные научные течения, порвавшие связь с основными физиче­скими воззрениями Фарадея и Максвелла, обходятся без этою представления и развивают формально-математические построения, основываясь на допущении действия на расстояние. Во введении и в первом параграфе настоящей книги была в достаточной степени охарактеризована эта точка зрения, принимаемая главным образом математиками, посвятившими себя решению вопросов из области физики.