1) См., например, и. В. Мещерский, „Теоретическая механика", ч. II.

²) Подробный вывод 2-й формы лагранжевых уравнений можно найти в III части курса проф. И. В. Мещерского „Теоретическая механика".

¹) В дальнейшем изложении из технических соображений будет приценяться обозначение q'.

²) В действительности мы будем дальше обозначать обобщенные силы через q,

Переводчик.

§ 93. Выражение для кинетической энергии в обобщенных

координатах.

Так как обобщенные координаты, как было выше указано, вполне определяют положение всех частей системы, то они должны быть связаны некоторыми зависимостями с декартовыми координатами всех точек системы. Следовательно, мы можем выразить декартовы координаты через обобщенные при помощи некоторых уравнений:

320

Всего таких уравнений будет 3s, где s — число точек системы, заданных декартовыми координатами.

С другой стороны, из механики известно, что кинетическая энергия системы выражается в декартовых координатах так:

Чтобы получить выражение для кинетической энергии в обоб­щенных координатах, надо в выражение (66) подставить значения x'_i, y'_i, z'_i. Последние найдем, если возьмем производные по вре­мени от уравнений (65):

Возведя полученные выражения в квадрат, мы получим, во-первых, члены, содержащие квадраты обобщенных скоростей, а во-вторых, члены с их удвоенными произведениями.

Произведя подстановку и собирая члены с одинаковыми обоб­щенными скоростями, получим окончательно для кинетической энергии системы в обобщенных координатах:

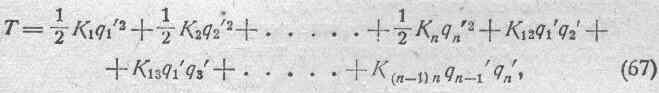
где коэффициенты К являются функциями обобщенных координат, но не их производных.

Таково выражение кинетической энергии всякой системы. В случае электродинамической системы, т. е. в случае системы токов, выражение для Т имеет тот же вид. Для составления этого выражения прежде всего обратимся к рассмотрению вопроса о вы­боре обобщенных координат для электродинамической системы.

§ 94. Выбор обобщенных координат для электродинамической системы.

Всякая электродинамическая система, вообще говоря, предста­вляет собою совокупность проводящих цепей, по которым проте­кают электрические токи, т. е. механическую систему, совмещенную с системой электрокинетической. Наличие электрических токов указывает на существование в системе какого-то специфического движения, отличающегося от обычного движения материальных

321

частей системы. Таким образом, при изучении системы токов мы должны считаться с двоякого рода движениями и силами: во-пер­вых, с силами чисто механическими, способными влиять на пере­мещения системы или ее элементов в пространстве (движения проводников), и, во-вторых, с перемещениями „электричества" и соответствующими им электродвижущими силами (явления собст­венно электрического тока).

При целесообразном выборе координат вторая форма уравне­ний Лагранжа дает возможность учесть оба рода явлений.

Характер происходящих процессов указывает, что необходимы две категории координат: геометрические и электрические.

Будем характеризовать данную систему проводящих цепей, рассматриваемую исключительно в качестве некоторой механической системы, геометрическими координатами g₁, g₂, g₃ и т. д.

Этими координатами определяется как положение всей системы в пространстве, так и взаимное расположение ее частей.

Для характеристики электрокинетического процесса Максвелл выбрал в качестве обобщенных координат количества электри­чества: q₁, q₂, q₃ и т. д., протекшие через поперечное сечение проводников, начиная от некоторого начального момента времени. Действительно, количество электричества, протекшего по данной цепи, в полной мере может охарактеризовать степень продвижения электрокннетического процесса. При этом в качестве обобщенной силы естественно принять электродвижущую силу е, которая яв­ляется реальной причиной возникновения всякого электрокинети­ческого процесса и в то же время удовлетворяет тому условию, чтобы произведение ее на приращение обобщенной координаты представляло собою работу (е•q).

Производные от электрических координат q по времени будут представлять собою электрические токи:

и т. д., т. е. сила электрического тока характеризует собою ско­рость некоторого кинетического процесса.

При указанном выборе обобщенных координат после надлежа­щего расположения по группам всех членов, входящих в выраже­ние кинетической энергии Т системы проводников, несущих элек­трические токи, получим:

т. е. кинетическая энергия изобразится в виде суммы трех групп членов: первой, представляющей собою функцию от геометриче­ских скоростей, второй, зависящей от электрических скоростей,

322

т. е. токов, и третьей, содержащей произведения геометрических и электрических скоростей.

Что касается коэффициентов А, В и С (частные значения коэф­фициентов K), то выше мы уже указали, что они зависят от самих обобщенных координат, но не от скоростей их.

Не трудно показать, что эти коэффициенты в данном случае содержат только геометрические координаты g₁, g₂, g₃ и т. д. Электрические же координаты q₁, q₂, q₃ и т. д. в эти коэффициенты не входят. В самом деле, предположим, что i₁, i₂ и т. д. постоянны и что все части системы неподвижны, т. е.:

i₁ = q₁=const, i₂=q₂=const и т. д. и

g'₁=0; g'₂=0 и т. д.

В таком случае кинетическая энергия системы будет содержать только члены с коэффициентами В, а именно:

Опыт показывает, что в этом случае кинетическая энергия системы, т. е. энергия системы токов, остается неизменною в те­чение сколь угодно большого промежутка времени, так как общие условия, характеризующие магнитное поле, в такой системе оста­ются без всякого изменения. Это возможно только тогда, когда коэффициенты B₁ В₂ и т. д. не зависят от изменяющихся электри­ческих координат q₁, q₂, . . . q_n.

323

Коэффициенты A₁, A₂ и т. д. не зависят от этих координат, так как сумма членов с этими коэффициентами представляет собою ки­нетическую энергию системы, рассматриваемой как совокупность материальных тел, не обладающих электрическими токами.

Что касается коэффициентов С, то надо думать, что и они не зависят от электрических координат q. Действительно, если пред­положить, что все токи в системе постоянны, т. е.

i₁=const; i₂=const и т. д.,

и вместе с тем допустить, что все части системы непрерывно со­вершают такого рода периодические движения, при которых гео­метрические координаты изменяются лишь в некоторых узких пределах, периодически повторяясь, то полная кинетическая энергия системы, как показывает опыт, претерпевает лишь некоторые периодические же изменения, не выходя за определенные пределы, между тем как электрические координаты q (количество протек­шего электричества) непрерывно и беспредельно растут. Если бы они входили в коэффициенты С, то можно было бы ожидать непре­рывного изменения суммарной кинетической энергии в каком-либо определенном направлении.

Таким образом, и коэффициенты С₁₁, C₁₂ C₁₃ и т. д. можно считать не зависящими от электрических координат q₁, q₂, q₃... q_n.

Итак, мы нашли общее выражение для кинетической энергии электродинамической системы. Оно производит впечатление слож­ного только потому, что мы взяли его в самой общем виде, для случая произвольного числа независимых переменных (обобщенных координат). Если же мы возьмем простейшие случаи, то соответ­ственно упростится и выражение для Т, Вторая форма уравнений Лагранжа чрезвычайно облегчает обследование электродинами­ческие явлений: зная выражение для кинетической энергии, мы легко можем получить выражение для всех сил, возникающих в си­стеме. При этой, так как силы здесь обобщенные, соответственно обобщенным координатам, то наше исследование не ограничится силами механическими. Перед нами открывается возможность все­стороннего исследования электродинамической системы.

Для облегчения этого исследования интересно предварительно проанализировать общее выражение кинетической энергии электро­динамической системы.