2) Maxwell, Treatise on El. And Magn., Vol II, § 569.

§ 74. Участие электрического поля в процессе электрического тока.

Основная мысль Фарадея относительно роли проводника, по которому течет ток, заключается, как было отмечено в предыдущем параграфе, в том, что проводник служит своего рода осью, вокруг которой надлежащим образом ориентированы электрические и маг­нитные силы. Развивая эту мысль дальше, Пойнтинг и Дж. Дж. Томсон остановились на предположении, что в процессе электрического тока главное значение имеют силы электрического характера, т. е. электрическое поле. Исходя из этого предположения, они разрабо­тали весьма стройную схему того кинетического процесса, который мы можем мыслить в пространстве, окружающем проводник с током. В тех случаях, когда в данной цепи или вообще в данной системе мы встречаемся с ясно выраженными электрическими зарядами и с электрическим полем, с ними связанным, схема Пойнтинга и Дж. Дж. Томсона весьма удобна и проста.

В виде первого примера рассмотрим случай возникновения электрического тока в проводнике, соединяющем два противо­положно заряженных тела, А и В (рис. 129).

Допустим, что эти тела заряжены одинаковыми количествами электричества обратных зна­ков, так что на теле А находится заряд +q, а на теле В — за­ряд -q. В пространстве, окружающем заряженные тела, мы будем иметь электрическое поле. Все фарадеевские трубки этого поля начинаются на теле А и заканчиваются на теле В. Система обладает определенным запасом энергии в виде энергии электрической де­формации диэлектрика. Этот запас выражается, как известно, ин­тегралом: ¹/₂∫EDdv, причем интегрирование распространено по всему пространству, где только существуют фарадеевские трубки рассматриваемой системы. Эта система, очевидно, пребывает в со­стоянии электрического равновесия до тех пор, пока тела А и В в достаточной степени изолированы и пока сила электрической упругости диэлектрика (см. § 47) вполне уравновешивает силу, которая создает в этой среде деформацию. Заметим еще, что но­сителями энергии в рассматриваемом случае, согласно теории Пойнтинга и Дж. Дж. Томсона, будут фарадеевские трубки, и система в целом не изменит своего состояния, пока будет сохраняться устойчивое равновесие всей совокупности фарадеевских трубок в электрическом поле.

Соединим теперь тела А и В металлическим проводником ab, идущим от тела А к телу В вдоль некоторой силовой линии, одно-

236

временно являющейся и осью соответствующей фарадеевской трубки. Пойнтинг доказал математически, что в этом случае геометрические формы поля не нарушаются. Но в системе про­изойдут существенные изменения вследствие нарушения бывшего до того равновесия. Новым фактором в электрическом поле является пространство в объеме проводника ab. Действительно, электрическая упругость металла ничтожно мала, и она не может уравновешивать силу, производящую деформацию, т. е. электрическую силу Е (cм. § 47). Благодаря этому электрическое смещение в объеме провод­ника исчезнет. Другими словами, должны будут исчезнуть фарадеевские трубки, оказавшиеся внутри объема, занимаемого провод­ником. Энергия электрической деформации, однако, исчезнуть не может, хотя бы носители ее — фарадеевские трубки — и исчезли. Эта энергия перейдет только в другую форму. Она превращается в тепло путем некоторого процесса, сопровождающегося приращением кинетической энергии мо­лекул вещества проводника ab. Описываемый процесс исчезно­вения деформации называют „расслаблением деформации", или „реляксацией". В материаль­ных системах мы часто встре­чаемся с подобным же явлением реляксации. Всем, например, из­вестна в этом отношении смола, называемая сапожным варом. Это — твердое тело, в котором, несомненно, можно вызвать уп­ругую деформацию, но только на очень короткий промежуток времени. Подобная деформация, как таковая, скоро исчезает вслед­ствие малой способности вара упруго сопротивляться внешней де­формирующей силе. Он уступает ей, течет.

После исчезновения фарадеевских трубок в объеме проводника ab процесс, однако, не закончится. Фарадеевские трубки, как известно (см. § 68), производят друг на друга боковое давление, или, дру­гими словами, между ними существует боковой распор. Если в од­ной части электрического поля исчезнут фарадеевские трубки, то вследствие того, что боковой распор трубок, извне приле­гающих к этой части пространства, не будет ничем уравно­вешиваться, в рассматриваемой системе равновесное состояние окажется нарушенным. Неуравновешенный распор фарадеевских трубок заставит их двигаться поперек их длины по направлению к части пространства, свободной от трубок. Поэтому фарадеевские трубки, находящиеся вне проводника ab, войдут в него извне и вновь заполнят его объем. За этим последует повторение только-что рассмотренного процесса реляксации электрической деформации в объеме проводника ab и т. д. и т. д. Таким образом, в простран­стве вокруг проводника ab возникает движение фарадеевских трубок

237

по направлению к проводнику, как показано стрелками на рис. 129, и одновременно с этим будет происходить поглощение трубок проводником, сопровождающееся их реляксацией, т. е. исчезновением. Появление новых трубок в проводнике будет иметь следствием не­прерывное возобновление деформация электрического смещения через любое поперечное сечение проводника, что эквивалентно не­прерывному течению электричества по проводнику. И если в одну секунду внутрь проводника войдет N фарадеевских трубок, то в то же время через поперечное сечение его протечет N единиц электри­чества, ибо электрическое смещение сквозь поперечное сечение каждой фарадеевской трубки равно единице.

Процесс перемещения фарадеевских трубок и непрерывного по­глощения их проводником ab будет продолжаться до тех пор, пока не иссякнет запас трубок в данной системе, т. е. пока вся энергия электрического поля не превратится в тепло, нагревающее про­водник. Результатом исчезания фарадеевских трубок является то, что потенциалы тел А и В между собою уравниваются, в конце концов делаются совершенно тождественными, и мы имеем:

U_A-U_B=0.

Опыт показывает, что рассматриваемый процесс исчезновения электрического поля, помимо выделения теплоты в веществе про­водника ab, сопровождается еще весьма характерным явлением: вокруг проводника наблюдается магнитное поле. Согласно воз­зрениям Дж. Дж. Томсона и Пойнтинга, представление о маг­нитном поле необходимо рассматривать как наш способ восприятия движения фарадеевских трубок. Согласно этой теории, фарадеевские трубки, перемещающиеся перпендикулярно своей длине, производят действия, обычно нами приписываемые особому состоянию среды, так называемому магнитному состоянию. При этом направление возникающего „магнитного поля", т. е. направление, характеризую­щее добавочное свойство среды, составляет прямой угол с напра­влением самих фарадеевских трубок и направлением их перемещения.

Представим себе теперь, что общая обстановка схемы, только-что нами рассмотренной и изображенной на рис. 129, будет до­полнена в том отношении, что к телам А и В извне будут непре­рывно подводиться новые электрические заряды и связанные с ними новые фарадеевские трубки, по мере того, как проводник ab будет поглощать запас энергии электрического поля системы, превращая его в тепло. В таком случае течение электричества в проводнике ab, сопровождаемое описанным выше движением фарадеевских тру­бок в пространстве вокруг проводника, может продолжаться не­определенно долго.

По Пойнтингу и Дж. Дж. Томсону, во всех генераторах или источниках электрической энергии происходит какой-то внутренний процесс, в результате которого возникают фарадеевские трубки, идущие изнутри источника и обусловливающие между зажимами генератора некоторую определенную разность потенциалов. Иными

238

словами, зажимы генератора играют для внешней цепи ту же роль, что и заряженные тела А и В в только-что разобранном случае (рис. 129).

В качестве более сложного примера того, как с точки зрения Пойнтинга и Дж. Дж. Томсона можно понимать механизм электри­ческого тока, остановимся на схеме передачи электрической энергии от некоторого генератора, скажем, от батареи аккумуляторов, по проводникам АА' и ВВ' к приемнику электрической энергии А'В', который можем в простейшем случае представить себе в виде ка­кого-либо полезного сопротивления R (рис. 130). Образующиеся в генераторе фарадеевские трубки, изображенные на рисунке тонкими сплошными линиями, под влиянием бокового распора рас­пространяются по окружающему пространству, опираясь своими концами на проводники (+ и -), которые идут от зажимов А и В.. Направление движения фарадеевских трубок показано большой стрелкой (от генератора к приемнику). Провода АА' и ВВ' являются при этом как бы направляющими для движущихся трубок. При движении трубки отдают часть своей энергии этим направляющим,, что осуществляется поглощением конечных участков трубок веще­ством проводника. В связи с этим разность потенциалов между концами каждой фарадеевской трубки уменьшается по мере удаления от генератора. И, наконец, дошедшие до приемника R участки фарадеевских трубок поглощаются им и обусловливают выделение в нем эквивалентного количества энергии в какой-либо иной форме (не электрической). Сказанное очень хорошо иллюстрируется, по Пойнтингу, путем построения системы равнопотенциальных поверхно­стей, которые на рис. 130 показаны пунктирными линиями (в се­чении плоскости рисунка).

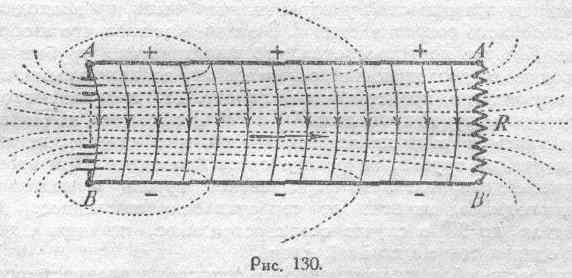
Если при этом построение данных по­верхностей произвести с таким расчетом, чтобы разность потенциалов между двумя соседними равнопотенциальными поверхностями была некоторой постоянной для данного случая величиной, то из рас­сматриваемого схематического рисунка можно вывести некоторые количественные заключения. Действительно, количество электри­ческой энергии, которою обладает данный участок фарадеевской трубки, численно равно (см. § 67) половине разности потенциалов

239

между концами этого участка, т. е.¹/₂(U₁-U₂). Следовательно, по­строенная указанным выше способом система равнопотенциальных поверхностей разбивает все фарадеевские трубки на ячейки, каждая из которых является носительницей одного и того же количества электрической энергии. Условия экономичности передачи энергии вдоль проводов АА' и ВВ' требуют, чтобы между генератором* и приемником расходовалось возможно меньше энергии. С рассматривае­мой точки зрения это означает, что провода АА' и ВВ' должны по­глощать возможно меньшее количество вышеупомянутых ячеек равной анергии, и возможно большее количество этих ячеек должно до­ходить до приемника R. Отсюда вытекает требование, чтобы равно-потенциальные поверхности в возможно большем количестве пере­секали полезное сопротивление и чтобы таких пересечений при­ходилось как можно меньше на долю проводов, передающих энергию, т. е. чтобы падение напряжения в этих проводах было возможно меньше. На рис. 130 это иллюстрируется соответствующим рас­положением поверхностей уровня: главная часть их приходится на долю полезного сопротивления R. В отличие от того, что изображено на рис. 129, где предполагается, что фарадеевские трубки входят в проводник их поглощающий, оставаясь ему параллельными, в схеме передачи энергии, представленной на рис. 130, процесс поглощения фарадеевских трубок проводами АА' и ВВ' необходимо, по Пойнтингу, представлять в виде последовательного, так сказать, втягивания концов каждой трубки, опирающейся на проводник. При этом угол, образуемый направлением фарадеевской трубки и направлением оси проводника, зависит от сопротивления последнего, доходя в пределе до 90° в случае сверхпроводников, потенциал которых будет один и тот же по всей длине.

Интересно обратить внимание на некоторые количественные соотношения, характеризующие рассматриваемую электрическую цепь с точки зрения энергетической. Допустим, что режим электрического тока в цепи вполне установился, т. е. что по ней протекает строго постоянный ток. Этот режим можно понимать, как состояние установившегося равновесия в системе: ежесекундно вся внешняя цепь в целом поглощает ровно столько фарадеевских трубок, сколько их вырабатывает генератор, в данном случае аккумуляторная ба­тарея АВ, Положим, что цепь поглощает N фарадеевских трубок в секунду. Как это явствует из предыдущего, число N определяет собою количество электричества, протекающего в одну секунду через поперечное сечение цепи, т. е. это именно и есть мера силы тока. Поэтому в данном случае можем написать:

i=dq/dt=N.

Обозначая через U_A-U_B разность потенциалов между зажимами А и В, получаем для мощности, расходуемой во внешней цепи, следующее выражение:

P=(U_A-U_B)i=(U_A-U_B)N.

240

Следовательно, каждая фарадеевская трубка, поглощаемая внешнею цепью, отдает ей количество энергии, равное (U_A-U_B) эргов, если мы все величины выражаем в абсолютной системе. В то же время мы знаем, что каждая фарадеевская трубка, в силу связанной с ней электрической деформации, является носительницей энергии, и это количество энергии есть ¹/₂ (U_A -U_B) эргов. Таким образом, из всей энергии, вносимой фарадеевской трубкой в объем поглощающего её проводника, только половина может быть объяснена тем запасом энергии, который присущ каждой трубке в силу электрической деформации среды. Согласно теории Пойнтинга, другая половина этой энергии есть энергия движения фарадеевских трубок, обычно нами воспринимаемая как энергия магнитного поля. Это находится в полном соответствии с упомянутой уже выше идеей Пойнтинга и Дж. Дж. Томсона, что представление о магнитном поле и есть лишь форма восприятия нами движения фарадеевских трубок. Подробнее об этом существовании электрического и маг­нитного поля в электромагнитных процессах мы будем говорить в главе VIII— „Движение электромагнитной энергии". Здесь ограни­чимся лишь констатированием того факта, что во всяком простран­стве, через которое распространяется электромагнитная энергия, всегда обнаруживаются как электрическое, так и магнитное поле.

Итак, мы познакомились с точкой зрения Пойнтинга и Дж„ Дж. Томсона на механизм того процесса, который происхо­дит в пространстве, окружающем проводник с током. Однако, как ни изящна сама по себе основная картина движения фарадеевских трубок, предположенная и развитая ими, есть целый ряд случаев, когда этой картиной никак удовлетвориться нельзя. Так, например, электромагнитную индукцию тока чрезвычайно трудно представить себе с точки зрения движения фарадеевских трубок, в особенности в простейшем случае движения проводника поперек магнитного поля, скажем, постоянного магнита. Не менее трудно постигнуть о этой точки зрения и само постоянное магнитное поле в случае, когда в нем не наблюдается никаких электрических сил, как это и будет в поле постоянного магнита. Попытки Дж. Дж. Томсона нарисовать схему механизма явления во всех этих случаях приводят к слишком сложным и маловероятным построениям, основанным на допущении, что мы можем одновременно иметь в пространстве две системы фарадеевских трубок, противоположно направленных, на­лагающихся одна на другую и двигающихся по противоположным направлениям.

Обратимся еще к случаю постоянного тока в цепи, изображен­ной на рис. 130. Представим себе, что где-либо вблизи проводника расположено некоторое проводящее тело, например, металлический шар. Ради простоты допустим, что магнитная проницаемость вещества шара равна единице. Внесение этого проводящего шара в электро­магнитное поле тока ни в малейшей степени не изменит характера магнитного поля в пространстве вокруг проводника с током. И в то же время совершенно несомненно, что в случае постоянного тока, протекающего по рассматриваемой цепи, внутри металлического

241

шара исчезнет электрическое поле. В объеме проводящего шара не будет ни электрического поля, ни фарадеевских трубок. Если продолжать стоять на точке зрения Пойнтинга и Дж. Дж. Томсона, то надо допустить, что вне шара продолжается прежнее движение фарадеевских трубок. Совершенно невозможно допустить, чтобы в объеме шара появились добавочные трубки, противоположно на­правленные и двигающиеся в противоположную сторону. Вообще, отсутствие электрического поля вокруг проводника с током может быть констатировано в целом ряде случаев, и все происходит так, как будто бы наличие этого поля не является характерным при­знаком процесса, происходящего вокруг проводника с током.

Полное отсутствие электрического поля во всех точках про­странства, окружающего проводник с током, может быть конста­тировано в случае тока, индуктированного в некоторой сверхпроводящей цепи, не заключающей в себе никаких частей, поглощающих электромагнитную энергию. По этой цепи будет протекать постоян­ный ток. Магнитное поле его будет неизменно. Потенциал всех точек сверхпроводящего контура будет один и тот же. В поле тока в этом случае не может быть никаких электрических сил. В связи с этим отметим, что в рассматриваемом случае в цепи тока нет никакого поглощения электромагнитной энергии. Запас этой энергии,

равный 1/₂Li² и представляющий собою энергию магнитного поля

тока (см. § 21), остается неизменным и недвижимым. Повидимому, электрическое поле вокруг проводника с током сопутствует магнитному полю только в тех случаях, когда в цепи вдоль про­водника движется электромагнитная энергия. В то же время магнитное поле есть совершенно неотъемлемый и безусловно всегда наблюдаемый признак того кинетического процесса, который мы называем электрическим током. На основании всего изложенного представляется более соответствующим основным , свойствам тока, строить вероятную схему механизма электрического тока, исходя из магнитного поля как первичного явления. Рассмотрению этого вопроса посвящен следующий параграф. В заключение же настоя­щего параграфа мы, однако, считаем долгом отметить несомненную простоту схем Пойнтинга и Дж. Дж. Томсона в тех случаях, когда мы встречаемся в процессе электрического тока с ясно выраженными зарядами как, например, в случае прохождения тока через газы и электролиты. Оставляя поэтому открытым вопрос о степени отношения этих схем к действительности, мы считаем все же весьма полезным применение их в указанных случаях, тем более, что получаемые таким путем количественные результаты, насколько об этом можно судить, вполне справедливы.