§ 65. Вторая формулировка теоремы Максвелла.

Так как электрическое смещение сквозь поперечное сечение фарадеевской трубки равно единице, то, следовательно, каждая такая трубка, пересекая некоторую поверхность, привносит в вели­чину полного электрического сме­щения сквозь эту поверхность свою долю, численно равную единице. Таким образом, в однородном электрическом поле смещение D в некоторой точке А (рис. 120)

численно равно количеству фарадеевских трубок, проходящих сквозь квадратный сантиметр поверхности, нормальной к вектору D (см. пунктирные линии на рис. 120). Обозначая через N₁ указанное количество трубок, можем поэтому написать:

d=n₁. (48) В случае неоднородного поля соотношение (48) примет вид:

D=dN/ds (49)

где dN есть количество фарадеевских трубок, проходящих сквозь элементарную площадку ds, нормальную к вектору D.

Вообще полное электрическое смещение сквозь любую поверх­ность выразится на основании вышеизложенного полным количе­ством (N) фарадеевских трубок, пересекающих рассматриваемую поверхность, т. е.

/ Dcosds=N. (50)

При подсчете числа N мы должны суммировать трубки алгебраи­чески, другими словами, необходимо обращать внимание на то, в каком направлении они пересекают поверхность. Все фарадеевские трубки, пересекающие поверхность в направлении избранной нор­мали к ней, считаются положительными; трубкам же, пересекающим ее в обратном направлении, приписываем знак минус.

Пользуясь соотношением (50) и прилагая его к произвольной замкнутой поверхности, мы можем сформулировать теорему Макс­велла (см. соотношение 31 в § 50) на языке фарадеевских трубок следующим образом:

N=Q, (51)

209

т. е. полное число фарадеевских трубок, пересекающих некоторую замкнутую поверхность в направлении внешней нормали, равно количеству электричества, находящегося внутри этой поверхности.

Для пояснения новой фор­мулировки теоремы Максвел­ла рассмотрим пример, представленный на рис. 121.

Здесь внутри замкнутой по­верхности 5 представлены три наэлектризованных тела с зарядами +10, -7 и -6. Ясно, конечно, что число фарадеевских трубок, исходя­щих с поверхности заряженного тела или заканчиваю­щихся на нем, в точности равно числу единиц электри­чества того или иного знака, составляющих заряд этого тела. Подсчитывая количество фарадеевских трубок, пересекающих данную замкнутую поверхность s в направлении внешней нормали, получаем;

N=+6-9=-3.

Полное же количество электричества, находящегося внутри 5, будет:

.Q=+10-7-6=-3,

что и показывает справедливость второй формулировки теоремы Максвелла в приложении к данному частному случаю.

§ 66. Электризация через влияние. Теорема Фарадея.

Так называемая электризация через влияние, т. е. возникновение электрических зарядов на нейтральном до того проводящем теле в случае поднесения его к какому-либо другому заряженному телу, представляется явлением естественно необходимым, если рассматри­вать его с точки зрения заполняющих электрическое поле фарадеев­ских трубок со всеми их свойствами. Действительно, представим себе некоторое тело А, заряженное, например, положительно (рис. 122). Во все стороны от тела А расходятся фарадеевские трубки. Под­несем теперь к телу А некоторое проводящее тело В, предвари­тельно не наэлектризованное. Части фарадеевских трубок, оказавшиеся при этом внутри тела В, не могут сохраниться, так как элек­трическая упругость проводника чрезвычайно мала и непрерывно „уступает" электрической силе (см. § 47). Дело в том, что раз­ность потенциалов, которая в первый момент будет существовать между началом и концом каждого участка фарадеевской трубки

210

внутри тела В, вызовет в нем появление уравнительных электриче­ских токов. Токи эти будут существовать внутри проводящего тела В до тех пор, пока не исчезнут какие бы то ни было разно­сти потенциалов между отдельными частями тела В. Тогда для всех точек его получим:

U=const.

При этом во всех точках внутри тела В будем иметь:

E=0 D = 0,

т. е. деформация электрического смещения в объеме тела В исчез­нет, и, следовательно, исчезнут в нем соответствующие части фарадеевских трубок. Джоулево тепло, развивавшееся в теле В под влиянием возникших в нем электрических токов, эквивалентно тому количеству энергии электрического поля, которое в начальный момент, при поднесении те­ла В к телу А, оказалось в объеме тела В в форме энер­гии упругой электрической деформации (§ 67).

Необходимо иметь в виду, что совершенно подобно то­му, как в случае магнитного поля магнитные линии стре­мятся пройти через тело с большой магнитной прони­цаемостью, например, через кусок железа, и сгущаются в нем, так же и в случае электрического поля мы встречаемся с аналогичной картиной. Фарадеевские трубки стремятся сгуститься в теле с сравнительно большой диэлектриче­ской постоянной. Это может быть объяснено наличием бокового распора в системе фарадеевских трубок (§ 68). Так как всякий проводник можно рассматривать как вещество с очень большой диэлектрической постоянной, то естественно, что общее расположе­ние фарадеевских трубок в поле вокруг заряженного тела А пре­терпит некоторое изменение в связи с приближением тела В, и в результате получится нечто подобное тому, что изображено на рис. 122.

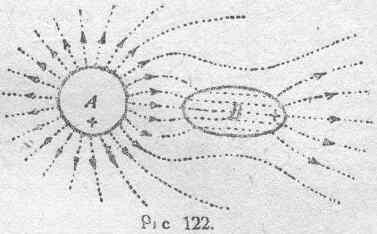
Пунктиром в объеме тела В на рисунке 122 показаны исчезнув­шие участки фарадеевских трубок. Мы видим, таким образом, что, благодаря поднесению тела В, некоторые из трубок, исходящих из тела А, претерпели разрыв. При этом они с одной стороны заканчи­ваются на теле В, и здесь мы обнаруживаем в данном случае отрицательную электризацию, а с другой стороны они отходят от тела В с той части его поверхности, которая наиболее удалена от тела А и на которой оказывается положительная электризация. Итак, мы видим, что всегда, при поднесении к заряженному телу некоторого предварительно не наэлектризованного проводника, на

211

этом последнем наводится (индуктируется) электричество обоих знаков: на стороне, обращенной к заряженному телу, — всегда про­тивоположного знака, а на другой стороне — того же знака, что и основной заряд. Вместе с тем алгебраическая сумма наведенных зарядов обязательно равна нулю, так как они образовались вслед­ствие разрыва фарадеевских трубок.

Рассуждения по поводу разобранного примера (рис. 122) остаются по существу теми же и во всех других случаях электри­зации через влияние. В частности, мы можем подобным образом весьма просто разобраться в том, что должно иметь место в известном опыте Фарадея, когда наэлектризованное тело вносится внутрь некоторой замкнутой камеры, стенки которой сделаны из проводящего мате­риала. Представим себе метал­лический изолированный сосуд В (рис. 123), установленный на изолирующей стойке К. Метал­лическая же крышка В' снаб­жена снизу крючком, к кото­рому на шелковой нити, пока­занной на рисунке пунктиром, подвешено тело А. Если со­суд В и его крышка В' вна­чале были не наэлектризованы и если, сняв крышку, наэлек­тризовать где-либо на стороне тело А, например, положительно и затем внести его внутрь со­суда В, то начальная картина расположения фарадеевских трубок, связанных с телом А, может быть схематически представлена так, как это изображено на рис. 123.

При этом все без исключения фарадеевские трубки будут перере­заны стенками сосуда и крышкой его. В толще стенок и крышки соответствующие участки трубок смещения исчезнут подобно тому, как это мы видели в случае рис. 122, и в результате на внутренней по­верхности проводящей камеры появляется (наводится) заряд, По абсо­лютной величине в точности равный заряду тела A, но обратного знака, а на наружной поверхности камеры—заряд и по величине и по знаку тождественный с зарядом тела А. Действительное окончательное распределение наведенных электрических зарядов на стенках камеры В, вообще говоря, будет несколько отличаться от схематически представленного на рис. 123, но количественные соотношения, к которым мы пришли, пользуясь свойствами фарадеевских трубок, всегда и неизменно сохраняют свою силу. Соотношения эти, впер­вые установленные Фарадеем, как результат опытного исследо­вания, мы будем называть, по предложению О. Д. Хвольсона, теоремой Фарадея. В общем виде теорема Фарадея, имеющая

212

большое значение в учении об электрическом поле, формулируется следующим образом:

Если произвольные наэлектризованные тела поместить внутрь проводящей замкнутой камеры, то одинаковые количества раз­ноименных электричеств, наведенных (индуктированных) на вну­тренней и на внешней поверхности, камеры, равны по абсолютной величине полному количеству электричества, находящегося на введенных в камеру телах, независимо от расположения этих тел.