1) Maxwell, Treatise on Electricity and Magnetism, Vol. I, § 45.

§ 60. Электрическая деформация среды.

С точки зрения Фарадея и Максвелла, участие промежу­точной среды в передаче электрических действий от одного наэлек­тризованного тела к другому, а также во всех вообще процессах, совершающихся в электрическом поле, столь же естественно и необходимо, как и в случае магнитных явлений. Как было выше отмечено (§§ 45 и 57), в обоих случаях мы имеем дело по суще­ству лишь с различными проявлениями одного основного процесса — электромагнитного. И вместе с тем мы имеем все основания рас­сматривать в качестве чего-то специфически характерного выну­жденное состояние диэлектрика, которое он приобретает, когда бывает подвергнут действию электрического поля. Это состояние диэлектрика, его электрическая деформация, и есть то, что Макс­велл назвал электрическим смещением:

и что всегда удовлетворяет соотношению, названному нами теоре­мой Максвелла:

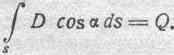
При изучении электрической деформации среды оказывается весьма удобным поступить так же, как и при изучении магнитного поля, а именно — расчленить объем диэлектрика на отдельные эле­менты, которые можно рассматривать, как носители всех основных свойств электрического поля. В нижеследующих параграфах мы и займемся этим.

§ 61. Линии смещения.

Линиями электрического смещения, или просто линиями сме­щения называются такие линии, построенные в электрическом поле, все элементы которых совпадают по направлению с векторами

204

электрического смещения D в тех местах, где рассматриваемые элементы линий расположены.

В среде однородной и изотропной вектор электрического сме­щения D совпадает по направлению с вектором электрической силы Е. Поэтому в такой среде силовые линии электрического поля и линии смещения совпадают. Таким образом, известные из физики картины и схемы Электрических силовых линий вместе с тем могут быть рассматриваемы и в качестве иллюстраций общего располо­жения линий смещения. Направление линии смещения определяется направлением вектора D, касательного к этой линии.

§ 62. Трубка смещения.

Трубкою смещения называется объем диэлектрика имеющий форму трубки, образующими которой служат линии смещения.

Рассмотрим некоторую трубку смещения в промежутке между двумя наэлектризованными телами, А и В (рис. 118), находящимися в состоянии электриче­ского равновесия.

Допу­стим, что тело А наэлек­тризовано положительно и тело В — отрицательно. Трубка смешения, опираясь своими концами на эти два тела, вырезает на их поверхностях площадки с расположенными на них зарядами q₁ и q₂. Обозна­чим через s₀ боковую по­верхность трубки и зам­кнем эту поверхность с концов двумя какими-либо поверхностями s₁ и s₂, которые можем себе представить внутри тела А и В. Получаем таким образом замкнутую поверхность s, состоящую из трех частей: s₀, s₁ и s₂. Приложим теперь к этой замкнутой поверхности теорему Максвелла:

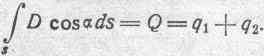
Здесь q₁+q₂ представляет собою алгебраическую сумму зарядов, находящихся внутри замкнутой поверхности s. Так как:

s=s₀+s₁+s₂,

то интеграл, изображающий полное электрическое смещение сквозь поверхность s, можно разбить на три составляющих:

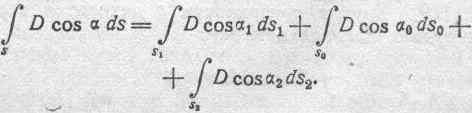
205

Остановимся прежде всего на величине первого и третьего интегралов в правой части этого равенства. Так как наэлектризован­ные тела А и В находятся согласно условию в состоянии электри­ческого равновесия, то можем написать:

U₁=const,

U₂=const.

В таком случае внутри каждого из этих тел градиент потенциала равен нулю, а следовательно, равны также нулю и электрическая сила Е и электрическое смещение D. Таким образом, нормальные составляющие электрического смещения для всех точек поверхно­стей s₁ и s₂ равны нулю и потому:

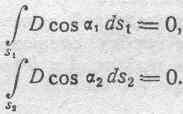
Что касается поверхности s₀, то вектор D будет касателен к ней во всех точках ее поверхности, ибо образующими этой поверх­ности являются линии смещения (см. § 61). Следовательно, для всех точек поверхности s₀ будем иметь

cos₀=0

и потому в этом случае также получаем:

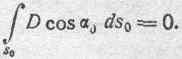
Итак, приходим к следующему результату:

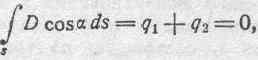
на основании чего окончательно получаем:

q₁=-q₂,

т. е. на концах трубки смещения находятся электрические зaряды, равные по абсолютной величине и обратные по знаку.

Рассмотрим теперь ту же самую трубчатую поверхность, но только в этом случае замкнем ее с одной стороны поверхностью s₁, внутри тела Л, и с другой стороны — произвольным сечением трубки s₃. Таким образом, полученная замкнутая поверхность s со­стоит в этом случае из s₁, части трубчатой поверхности s₀ и сече­ния s₃ (рис. 119).

Внутри поверхности s находится заряд q₁. На основании теоремы Максвелла имеем:

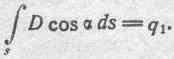
206

Далее можно написать, как и в предыдущем случае:

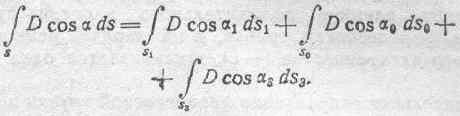
Как выше было доказано, два первых интеграла правой част» последнего равенства порознь равны нулю. На основании этого

получаем:

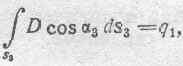
т. е. полное электрическое смещение сквозь поперечное сечение трубки смещения есть величина, неизменная для всех сечений и равная заряду, находя­щемуся в начале трубки. Выведенные основные свойства трубок смеще­ния показывают, что труб­ки можно рассматривать как струи, вдоль кото­рых мы должны мыслить течение электричества в процессе установления максвелловской деформа­ции электрического сме­щения. Вместе с тем, вследствие тесной связи между трубками смещения и находящимися у их концов зарядами, представление о трубках смещения позволяет" очень удобно и просто установить важнейшие количественные соотношения между свойствами электрического поля и соответствую­щими ему электрическими зарядами, так или иначе распределен­ными в поле.