§ 58. Закон Кулона и вытекающие из него определения и соотношения.

В настоящем параграфе мы даем краткую сводку основных определений и соотношений, относящихся к электрическому полю я вытекающих из закона Кулона. В первую очередь, конечно, напомним формулировку этого исходного закона.

а) Закон Кулона. Сила механического взаимодействия между двумя количествами электричества, q₁ и q₂, находящимися в двух точках на расстоянии r одно от другого, в любой однородной среде, направлена вдоль прямой, соединяющей эти точки, и выражается следующим образом:

где k есть коэффициент пропорциональности, зависящий от выбора единиц и от свойств среды.

В абсолютной электростатической системе единиц принимают для пустоты k численно равным единице.

В таком случае закон Кулона для пустоты численно прини­мает следующий вид:

192

Для всякой однородной и изотропной среды, как показывает опыт,

k=1/,

где  есть диэлектрическая постоянная среды. И закон Кулона для однородной и изотропной среды выражается таким образом:

Ясно, что диэлектрическая постоянная пустоты, обозначаемая специальным символом ₀, в абсолютной электростатической системе единиц принимается равной единице, т. е. мы имеем:

₀=1.

Точная же формулировка закона Кулона для случая пустоты получает следующий вид:

б) Единица количества электричества. Обращаясь к формули­ровке закона Кулона для пустоты и полагая:

q₁=q₂=q, f=1, r=1, а также принимая во внимание соотношение:

₀=1,

получаем:

q=1,

т. е. за единицу количества электричества в абсолютной электро­статической системе единиц принимается такое количество электри­чества, которое в пустоте взаимодействует с силою, равною одной дине, с другим таким же количеством, расположенным на расстоянии одного сантиметра от первого.

Абсолютная электростатическая единица количества электри­чества связана следующим образом с абсолютной электромагнитной единицей и с практической электромагнитной единицей количества электричества, т. е. с кулоном:

1 абс. эл.-магн. ед. кол. электр.=3•10¹⁰ абс. эл.-стат. ед. кол. электр.

1 кулон=3•10⁹ абс. эл.-стат. ед. кол. электр.

Количество электричества, или электрический заряд, представляет собою некоторую физическую сущность, с которою мы в действи­тельности встречаемся на опыте. Если это сравнить с тем, что го­ворилось выше (§ 31) о магнитных массах, то станет достаточно ясно, что необходимо относиться с известной осторожностью к тем формальным сближениям между электрическим и магнитным полями, которые являются результатом применения в обоих случаях закона Кулона, как исходного положения. Хотя с формальной стороны

193

есть много общего между электрическим полем и полем магнитным и хотя они по природе своей теснейшим образом связаны основным электромагнитным процессом, тем не менее это—различные сто­роны основного процесса. Мы пользуемся при формальном описании этих полей аналогичными определениями и понятиями. Не следует забывать, что физическое содержание этих понятий в обоих слу­чаях совершенно различно.

в) Электрическая сила или напряженность электрическою поля (Е). Рассмотрим электрическое поле в пустоте. Если / есть механическая сила, действующая на количество положительного электричества q, помещенное в некоторой точке, то электрическая сила в данной точке определяется по величине и направлению следующим соотношением:

E=f/q,

причем предполагается, что помещение заряда q в данной точке не изменяет общего распределения электрических зарядов в системе. Таким образом, можно ска­зать, что электрическая сила в не­которой точке измеряется меха­нической силой, которую испытывала бы в этом месте единица по­ложительного электричества. Эле­ктрическая сила есть вектор.

Все оговорки, сделанные в пункте в параграфа 2 относительно определения магнитной силы, в полной мере сохраняют свое значение и при определении электрической силы с соответствующей, конечно, заменой магнитных величин электрическими.

г) Силовыми линиями электрического поля называются такие линии, все элементы которых совпадают по направлению с векто­рами электрической силы в тех точках поля, где эти элементы расположены.

д) Электрический потенциал (U). Рассмотрим некоторую точку A, расположенную в электрическом поле (рис. 117).

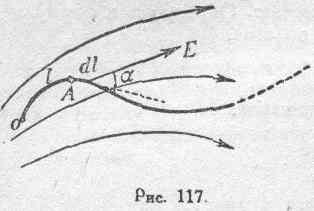
Пусть произволь­ная линия ОА продолжается от точки А в бесконечность. Возьмем линейный интеграл электрической силы Е от точки А вдоль этой линии до бесконечности:

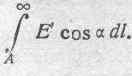
Здесь а есть угол между направлением элементарного пере­мещения dl и вектором Е. Подинтегральная величина Ecosdl чис­ленно равна работе перемещения единицы положительного электри­чества вдоль пути dl, а весь интеграл представляет собою работу, совершаемую силами электрического поля при перемещении еди­ницы положительного электричества (q=+1) по данному пути из

194

точки А в бесконечность. Величина этого интеграла, вообще говоря, может зависеть от выбора пути перехода из точки А в бесконеч­ность. Так бывает, между прочим, всегда, когда в пространстве, в котором мы рассматриваем данное электрическое поле, проис­ходит электромагнитный процесс, связанный, например, с измене­ниями магнитного поля и с движением магнитных линий (см. § 59). Есть, однако, случаи, когда никаких явных электромагнитных про­цессов в поле не наблюдается, и все происходит так, как будто бы электрическое поле обусловлено только наличием электрических зарядов, так или иначе распределенных в системе. Такие случаи характеризуются независимостью величины линейного интеграла электрической силы от пути перехода. Поле, в котором соблюдается подобное условие, обычно именно и называется электростати­ческим. Итак, в электростатическом поле величина интеграла

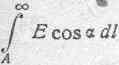
имеет для каждой точки поля вполне определенное

значение. Это значение линейного интеграла электрической силы является мерой напряженности электрического состояния в точке А и называется электрическим потенциалом точки А. Его обычно обозначают знаком U. Таким образом, можем написать:

Как известно, в электростатическом поле потенциал любой точки может быть также вычислен в зависимости от распределения электри­ческих зарядов в системе. Именно, в среде однородной и изотропной

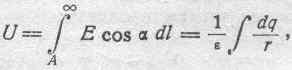
где dq есть элемент электрического заряда и r — расстояние его от данной точки А, причем во втором интеграле операция интегри­рования распространена на все электрические заряды, с которыми связано рассматриваемое электрическое поле.

Единица потенциала в абсолютной электростатической системе не имеет специального названия. Практическая электромагнитная единица потенциала называется вольтом. Связь между ними выра­жается следующим соотношением:

1 вольт =¹/₃₀₀ абс. эл.-стат. единицы потенциала.

Электрический потенциал, вообще говоря, различен для раз­личных точек поля и является функцией геометрических коорди­нат точки, т. е. U=f(x, у, z).

Эту функцию обычно называют потенциальной функцией, и электрический потенциал некоторой точки можно в таком случае определите как значение потенциальной функции в данной точке.

195

Кроме электростатического поля, есть еще и другие случаи, когда линейный интеграл электрической силы можно считать не зависящим от выбора линии интегрирования, при соблюдении, од­нако, некоторых специальных условий, которые должны быть особо оговорены. И в этих случаях можно еще пользоваться представле­нием об электрическом потенциале, как о некоторой определенной физической величине (см. § 59).

При изложении дальнейших пунктов настоящего параграфа мы будем иметь в виду всякое вообще электрическое поле, в пределах которого представление об однозначном электрическом потенциале сохраняет физический смысл.

е) Поверхности уровня или равнопотенциальные поверхности. Приравняем потенциальную функцию к какой-либо постоянной ве­личине, т. е. положим:

U=(x, у, z)=const. (36)

Мы пришли, таким образом, к уравнению некоторой поверх­ности, все точки которой имеют один и тот же потенциал. Это и есть поверхность уровня, или равнопотенциальная поверхность. Придавая потенциалу U различные частные значения, например 1, 2, 3 или 100, 200, 300 и т. д. вольт, можно получить целый ряд поверхностей уровня, расположение которых характеризует элек­трическое поле в той же мере, как и система силовых линий. О связи поверхностей уровня с силовыми линиями см. следующий пункт „ж".

ж) Градиент, потенциала. Рассмотрим некоторый путь перехода от точки А в бесконечность (рис. 117). Допустим, что положение точки А на этом пути определяется расстоянием l от начальной .точки О. В таком случае можем написать:

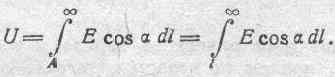
Взяв частную производную от обеих частей этого равенства но нижнему пределу, получаем:

или

Это означает, что составляющая электрической силы в данной точке по какому-либо направлению равняется взятой с обратным знаком производной потенциала по этому направлению. Так как направление l было избрано совершенно произвольно, то, обозначая

196

через Е_х, Е_у и Е_z составляющие электрической силы Е вдоль ко­ординатных осей, можем, следовательно, написать:

Если направление l изберем вдоль вектора Е, то будем иметь:

cos=1,

и соотношение (37) обращается в следующее:

Очевидно, в последнем случае мы имеем наибольшее возможное

значение дU/дl. знак минус показывает, что положительное направле­ние вектора Е есть то, в котором потенциал уменьшается.

Если направление l избрать перпендикулярно вектору Е, т. е. по­ложить: =90º, то получим:

откуда получаем:

U=const

Отсюда следует, что, избрав направление l, перпендикулярное вектору Е, мы перемещаемся вдоль поверхности уровня. Таким образом, приходим к заключению, что поверхности уровня нор­мальны по отношению к силовым линиям. И обратно, в каждой точке электрического поля электрическая сила Е нормальна к по­верхности уровня, проходящей через эту точку.

На основании всего изложенного, избирая за направление l на­правление вдоль нормали к поверхности уровня в данной точке, можем написать:

т. е. электрическая сила в данной точке равна взятой с обратным знаком производной потенциала по нормали к поверхности уровня в этой же точке.

Величину дU/дn, т. е. наибольшее значение возрастания потенциала,

рассчитанное на единицу перемещения, называют градиентом потенциала и обозначают символом gradU. Таким образом,

197

Градиент потенциала есть вектор, направленный в сторону воз­растания потенциала. Практически градиент потенциала выражают л вольтах на сантиметр.

Из сопоставления (39) и (40) получаем:

Е=-gradU. (41)

з) Теорема Гаусса. Выведенная в глазе I теорема Гаусса для магнитного поля формально может быть распространена и на элек­трическое поле (см. примечание стр. 45). На основании указанного можем написать для случая пустоты:

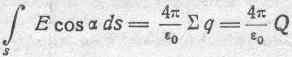
и для случая однородной и изотропной среды вообще:

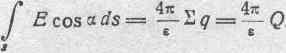
и) Теорема Пуассона. Допустим, что в однородной и изотроп­ной среде с диэлектрической постоянной  распределено электри­чество с объемною плотностью , являющеюся функцией геометри­ческих координат х, у, z. Рассмотрим теперь элементарный объем dxdydz и приложим к нему теорему Гаусса. Левую часть соотно­шения, изображающего эту теорему, можно представить состоящею из шести слагаемых, соответственно шести граням параллелепи­педа dxdydz. Интересующие нас площадки будут равны dydz каждая, Если составляющая электрической силы Е вдоль оси х-ов для всех точек одной из двух площадок есть Е_х, то можно положить для этой площадки:

Ecos=-Е_х.

В таком случае для другой площадки необходимо принять:

и часть интеграла:

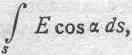
соответствующая рассматриваемым двум площадкам, получит сле­дующий вид:

Подобным же образом найдем две другие суммы для двух осталь­ных пар граней:

и

198

На основании этого, пользуясь теоремой Гаусса, можем напи­сать:

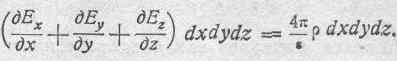
Отсюда получим:

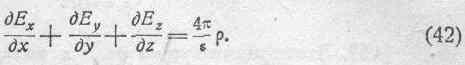
Полагая =₀ (для случая пустоты), приводим выражение (42) к виду:

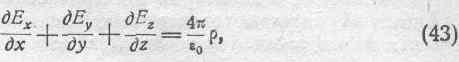
что собственно и составляет теорему Пуассона.

Принимая во внимание соотношение (38) пункта „ж" настоя­щего параграфа, можем ввести следующие преобразования:

н соотношения (42) и (43) принимают следующий вид:

Сумму вторых производных какой-либо функции по трем пере­менным х, у, z принято обозначать знаком А. Тогда соотношения (42') и (43') можно представить так:

к) Теорема Лапласа. Во всех точках пространства, где объемная плотность электричества равна нулю, имеет место следующее со­отношение:

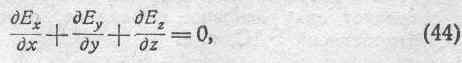
которое, как это явствует из предыдущего, может быть предста­влено еще в следующих формах:

199

или

U=0. (44")

Теорема Лапласа вытекает как следствие из соотношения (42), если в нем положить:

=0.