МОДУЛЬ 1.8. АНАЛИЗ ЗАВИСИМОСТЕЙ СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ

Цель изучения модуля: показать значение зависимостей между статистическими показателями для изучения общественного здоровья, деятельности системы (организаций) здравоохранения, в клинической практике.

После изучения темы студент должен знать:

- типы зависимостей между статистическими показателями;

- непараметрические методы оценки корреляционной зависимости;

- методику расчета, анализа и интерпретации выявленных зависимостей между статистическими показателями.

Студент должен уметь:

- установить тип зависимости между статистическими показателями;

- выбрать тот или иной тип зависимости между статистическими показателями при анализе общественного здоровья и деятельности системы (организаций) здравоохранения;

- рассчитать выборочный коэффициент корреляции;

- провести оценку корреляционной зависимости с помощью непараметрических методов;

- использовать полученные знания при обучении на клинических кафедрах.

1.8.1. Блок информации

Типы зависимостей. Многие прикладные задачи, например изучение причинно-следственных связей факторов риска и заболеваемости населения, требуют установления вида зависимости между показателями, которые выступают как случайные величины. Сама постановка множества задач в различных медико-социальных исследованиях предполагает построение и реализацию алгоритмов «фактор-отклик», «доза-эффект».

Случайные величины X и Y могут быть независимыми либо зависимыми.

Зависимость случайных величин называют стохастической (статистической), если изменение одной из них приводит к изменению закона распределения другой. Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то стохастическую зависимость называют корреляционной (например, зависимость заболеваемости населения от воздействия внешних факторов - эколого-гигиенических (климатические факторы, содержание различных соединений в атмосферном воздухе, воде, почве, пищевых продуктах), медико-организационных (уровень диспансеризации населения, обеспеченность больничными койками, медицинским персоналом) и т.д.). Сами случайные величины, связанные корреляционной зависимостью, оказываются коррелированными. При корреляционной зависимости Y и X возможно наблюдать тенденцию роста: с увеличением значений Х среднее значение Y возрастает или с увеличением значений Х среднее значение Y уменьшается. В этих случаях говорят соответственно о положительной или отрицательной корреляции.

Выборочный коэффициент корреляции. Как известно, степень зависимости случайных величин Х и Y (двух признаков) характеризуется значением коэффициента корреляции:

где K(X, Y) - корреляционный момент (ковариация) случайных величин X и Y, D(X) и D(Y) - дисперсии случайных величин.

Отметим, что всегда -1   r  1. Чем больше значение r отличается от нуля, тем сильнее зависимость X и Y. Если |r| = 1, то случайные величины X и Y связаны линейной функциональной зависимостью, Y = аХ + b, причем при r = -1 коэффициент а <0 (зависимость X и Y обратная), а при r = 1 коэффициент а >0 (зависимость X и Y прямая).

При этом коэффициент корреляции, как и всякая другая теоретическая характеристика, вычисляется, исходя из всех возможных значений Хи Y. На практике мы не имеем возможности охватить наблюдениями все указанное множество, а используем лишь ограниченное число наблюдений: двухмерную выборку¹ значений (x, y). Полученные числа можно занести в таблицу.

Таблица. Запись двумерной выборки

По данным наблюдений можно вычислить значение коэффициента корреляции так же, как и в случае системы дискретных случайных величин, с той лишь разницей, что вместо известных вероятностей для каждой пары возможных значений будем использовать соответствующий аналог: относительную частоту 1/n. Формула для вычисления выборочного коэффициента корреляции генеральных совокупностей (случайных величин) X и Y, исходя из двухмерной выборки, выглядит так:

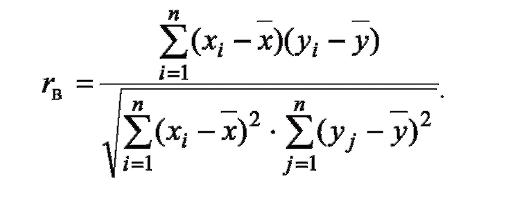
Если наблюдения объединяются по интервалам, т.е. все значения, попавшие в интервал, округляются до значения середины интервала, то каждая из наблюдаемых пар значений может встретиться неоднократно. В этом случае обычно данные заносят в таблицу с учетом частот встречаемости. Такую таблицу сгруппированных данных называют корреляционной.

Выборочный коэффициент корреляции r_B - оценка коэффициента корреляции r, рассчитанного по всей генеральной совокупности, т.е. r_B ≈ r. Следовательно, рассчитав r_B, можно судить о силе линейной связи. В случае если выборка имеет достаточно большой объем n, порядка сотен, то целесообразно воспользоваться r_B как точечной оценкой коэффициента корреляции r.

¹ Отметим, что в случае двумерной выборки значения случайных величин Х и Y располагаются не произвольно, а в соответствии с номером испытания i,т.е. каждому x_i соответствует y_i.

Непараметрические методы оценки корреляционной зависимости.

Приведем ряд характеристик, оценивающих тесноту связи различных факторов (признаков), причем не только количественных, но и качественных. В простейшем случае это признаки, представленные двумя альтернативными исходами типа «да-нет», «жив-умер», «заболел- не заболел» и т.д. Показатели тесноты связи вычисляются с использованием таблиц сопряженности.

Таблица. Сопряженность признаков

Для характеристики тесноты связи между признаками используются коэффициент ассоциации Юла и коэффициент контингенции Пирсона.

Коэффициент ассоциации Юла (KJ в соответствии с приведенной таблицей рассчитывают по формуле:

Коэффициент ассоциации К_а может принимать значения от -1 до +1. В случаях когда К_а = ±1, теснота связи между признаками считается наиболее сильной, причем так же, как и для коэффициента корреляции, положительный или отрицательный знак К_а свидетельствует о прямой или соответственно обратной зависимости значений признаков.

Коэффициент контингенции Пирсона К_к рассчитывают по формуле:

Коэффициент контингенции также изменяется от -1 до +1, но его значения всегда (за исключением граничных случаев K_K = ±1)

несколько меньше значений коэффициента ассоциации. Эта характеристика имеет тот же смысл, что и K_a.

Для качественной оценки силы связи при использовании коэффициента ассоциации Юла и коэффициента контингенции Пирсона можно руководствоваться шкалой Чеддока.

Таблица. Шкала Чеддока

В случае когда каждый из двух качественных признаков содержат более двух групп значений, тесноту связи признаков измеряют с помощью коэффициента взаимной сопряженности,который рассчитывается по специальным формулам¹.