
- •Глава I предмет и значение логики
- •§ 1. Формы познания Формы чувственного познания
- •Формы абстрактного мышления
- •Особенности абстрактного мышления
- •§ 2. Понятие логической формы и логического закона
- •Понятие логической формы
- •Логические законы
- •Истинность мысли и формальная правильность рассуждений
- •4. Все ушастые тюлени – ластоногие.
- •Теоретическое и практическое значение логики
- •§ 3. Логика и язык
- •Семантические категории
- •Задачи к теме “Предмет и значение логики”
- •Глава II понятие
- •§ 1. Понятие как форма мышления
- •Содержание и объем понятия
- •Закон обратного отношения между объемами и содержаниями понятий
- •§ 2. Отношения между понятиями
- •Типы совместимости: равнозначность (тождество), перекрещивание, подчинение (отношение рода и вида)
- •Типы несовместимости: соподчинение, противоположность, противоречие
- •§ 3. Определение понятий
- •Правила явного определения. Ошибки, возможные в определении
- •Неявные определения
- •Определение через аксиомы
- •Использование определений понятий в процессе обучения
- •Приемы, сходные с определением понятий
- •§ 4. Деление понятий. Классификация
- •Правила деления понятий
- •Виды деления: по видообразующему признаку и дихотомическое деление
- •Классификация
- •Использование естественных классификаций в школах и педагогических средних и высших учебных заведениях
- •§ 5. Ограничение и обобщение понятий
- •II. Определить отношения между следующими понятиями:
- •Глава III суждение
- •§ 1. Общая характеристика суждения
- •Суждение и предложение
- •§ 2. Простое суждение
- •Виды простых ассерторических суждений
- •1. Суждения свойства (атрибутивные).
- •2. Суждения с отношениями.
- •Категорические суждения и их виды (деление по количеству и качеству)
- •Объединенная классификация простых категорических суждений по количеству и качеству
- •Распределенность терминов в категорических суждениях
- •§ 3. Сложное суждение и его виды. Исчисление высказываний
- •Способы отрицания суждений
- •Отрицание сложных суждении
- •Исчисление высказываний
- •§ 4. Выражение логических связок (логических постоянных) в естественном языке
- •§5.Отношения между суждениями по значениям истинности
- •Противоположность (контрарность)
- •§ Б. Деление суждений по модальности
- •Задачи к теме “Суждение”
- •VII. Являются ли суждениями следующие предложения?
- •Глава IV законы (принципы) правильного мышления
- •§ 1. Понятие логического закона
- •§ 2. Законы логики и их роль в познании Закон тождества
- •Закон непротиворечия
- •Закон исключенного третьего
- •Специфика действия закона исключенного третьего при наличии “неопределенности” в познании
- •Закон достаточного основания
- •§ 3. Использование формально-логических законов в процессе обучения
- •Задачи к теме “Законы (принципы) правильного мышления”
- •Глава V умозаключение
- •§ 1. Общее понятие об умозаключении
- •Понятие логического следования
- •§ 2. Дедуктивные умозаключения
- •Понятие правила вывода
- •§ 3. Выводы из категорических суждений посредством их преобразования
- •S есть р
- •§ 4. Простой категорический силлогизм1
- •Фигуры и модусы категорического силлогизма
- •Особые правила фигур
- •Модусы категорического силлогизма.
- •Правила категорического силлогизма
- •/. Правила терминов
- •//. Правила посылок
- •§ 5. Сокращенный категорический силлогизм (энтимема)
- •§ 6. Сложные и сложносокращенные силлогизмы: (полисиллогизмы, сориты, эпихейрема)
- •Все с суть d. Сорит (с общими посылками)
- •Все а суть в. Все в суть с. Все с суть d.
- •Формализация эпихейрем с общими посылками
- •Выводы, основанные на логических связях между суждениями (выводы логики высказываний)
- •§ 7. Условные умозаключения
- •I. Утверждающий модус (modus ponens).
- •II. Отрицающий модус (modus tollens).
- •Первый вероятностный модус
- •Структура его: Cхема:
- •Второй вероятностный модус
- •§ 8. Разделительные умозаключения
- •§ 9. Условно-разделительные (лемматические) умозаключения
- •Дилемма1
- •Cхема Формула:
- •Трилемма
- •§ 10. Сокращенные условные, разделительные и условно-разделительные умозаключения
- •1. В умозаключении пропущено заключение
- •2. В умозаключении пропущена одна из посылок
- •1. Простая контрапозиция.
- •2. Сложная контрапозиция.
- •§ 11. Непрямые (косвенные) выводы
- •1. Рассуждение по правилу введения импликации
- •2. Правило сведения “к абсурду”
- •3. Правило непрямого вывода - рассуждение “от противного” (противоречащего)
- •§ 12. Индуктивные умозаключения и их виды Логическая природа индукции
- •Математическая индукция
- •Виды неполной индукции
- •2. Индукция через анализ и отбор фактов
- •Понятие вероятности
- •3. Научная индукция
- •§ 13. Индуктивные методы установления причинных связей Понятие причины и следствия
- •Методы установления причинной связи
- •Метод сходства
- •Если изменение одного обстоятельства всегда вызывает изменение другого, то первое обстоятельство есть причина второго. Метод остатков
- •Если известно, что причиной исследуемого явления не служат необходимые для него обстоятельства, кроме одного, то это одно обстоятельство и есть, вероятно, причина данного явления.
- •§ 14. Дедукция и индукция в учебном процессе
- •Задачи к теме “Умозаключение”
- •3. Во всех городах за полярным кругом бывают белые ночи.
- •Глава VI логические основы теории аргументации
- •§ 1. Понятие доказательства
- •Структура доказательства: тезис, аргументы, демонстрация
- •Виды аргументов
- •§ 2. Прямое и непрямое (косвенное) доказательства
- •§ 3. Понятие опровержения
- •1. Опровержение тезиса (прямое и косвенное)
- •II. Критика аргументов
- •III. Выявление несостоятельности демонстрации
- •§ 4. Правила доказательного рассуждения. Логические ошибки, встречающиеся в доказательствах и опровержениях
- •Правила по отношению к тезису
- •Ошибки относительно доказываемого тезиса
- •Правила по отношению к аргументам
- •Правило по отношению формы обоснования тезиса (демонстрации)
- •Ошибки в форме доказательства
- •3. Нарушение правил умозаключений (дедуктивных, индуктивных, по аналогии);
- •§ 5. Понятие о софизмах и логических парадоксах
- •Понятие о логических парадоксах
- •Парадоксы теории множеств
- •§ 6. Искусство ведения дискуссии
- •Задачи к теме
- •1Ушинский к. Д. Соб. Соч. М.-л., 1948. Т. 1. С. 397.
- •1Цит. По: Русская литература. Л., 1980. С. 55.
- •2Huкoлa Себастьен де Шамфор. Из максим и мыслей, афоризмов и анекдотов // Пер. С франц. Орел. 1991. С. 45,47-49.
- •3Смаллиан р. Как же называется эта книга? // Пер. С англ. М., 1981. С. 74,123.
- •Глава VII аналогия и гипотеза. Их роль в учебном процессе
- •§ 1. Умозаключение по аналогии и его виды
- •Строгая аналогия
- •Нестрогая аналогия
- •Ложная аналогия
- •§ 2. Гипотеза и ее виды
- •Виды гипотез
- •§ 3. Построение гипотез
- •Способы подтверждения гипотез бывают такие:
- •Примеры гипотез, применяющихся на уроках в школе
- •Глава VIII роль логики в процессе обучения
- •§ 1. Логическая структура вопроса
- •Виды вопросов
- •Предпосылки вопросов
- •Правила постановки простых и сложных вопросов
- •Логическая структура и виды ответов
- •§ 2. К. Д. Ушинский и в. А. Сухомлинский о формировании логического мышления в процессе обучения в начальной школе
- •§ 3. Развитие логического мышления младших школьников
- •Обобщение:
- •Ограничение:
- •§ 4. Развитие логического мышления учащихся в процессе обучения в средних и старших классах Развитие логического мышления учащихся на уроках литературы (из опыта о. Ю. Богдановой)
- •Развитие логического мышления на уроках математики
- •Глава IX методика преподавания логики в педагогических высших и средних учебных заведениях и школах
- •§ 1. Формирование логической культуры как условие гуманитаризации педагогического образования
- •Формы активизации мыслительной деятельности , студентов в учебном процессе
- •Семинары и самостоятельные работы студентов
- •РРис.23
- •2.Все птицы имеют оперение.
- •Контрольные работы
- •Вопросы экзаменационных билетов
- •Кроссворд по теме “Понятие”
- •Ответы на кроссворд
- •Формы внеаудиторной работы со студентами
- •§ 2. Специфика методики преподавания логики в средних педагогических учебных заведениях: педучилищах, педколледжах, подклассах (из опыта работы)
- •Кроссворд, составленный ученицей 11 класса Татьяной и.'
- •Ответы на кроссворд
- •По горизонтали:
- •Ответы на кроссворд
- •Тест айзенка (стр. 342-358)
- •§ 3. Методика повышения логической культуры учащихся начальной и средней школы (из опыта работы)
- •II. Требования к оформлению работы
- •1. В письменном отчете о проведенной педпрактике по логике необходимо описать проведенные занятия с учащимися и сделать приложение по следующей схеме (см. Табл., с. 361).
- •1См.: Гетманова а.Д. Учебник по логике. Серия “Российский лицей”. М.,1994. С. 54-57.
- •Задания по логике для студентов второго курса на период педагогической практики в 1987/88 учебном году
- •Глава X этапы развития логики как науки
- •§ 1. Краткие сведения из истории классической и неклассических логик
- •Логика в Древней Индии
- •Логика Древнего Китая
- •Логика в Древней Греции
- •Логика в средние века
- •Логика эпохи Возрождения и Нового времени'
- •Логика в России
- •Математическая логика
- •§ 2. Развитие логики в связи с проблемой обоснования математики
- •§ 3. Интуиционистская логика
- •§ 4. Конструктивные логики
- •Конструктивные исчисления высказываний в. И. Гливенко и а. Н. Колмогорова
- •Конструктивная логика а. А. Маркова
- •§ 5. Многозначные логики
- •Трехзначная система Лукасевнча
- •Отрицание Лукасевича
- •Трехзначная система Гейтинга
- •Импликация Гейтинга
- •Две бесконечнозначные системы Гетмановой:
- •§ 6. Законы исключенного третьего и непротиворечия в неклассических логиках (многозначных, интуиционистской, конструктивных)
- •§ 7. Модальные логики
- •§ 8. Положительные логики
- •§ 9. Паранепротиворечивая логика
- •Заключение
- •1. Предмет и значение логики.
- •2. Понятие.
- •3. Суждение.
- •4. Умозаключение.
- •5. Логические основы теории аргументации.
- •Список символов
- •Логика классов
§ 5. Многозначные логики
В многозначных
логиках число значений истинности
аргументов и функций для высказываний
может быть любым конечным (больше
двух) и даже бесконечным. В настоящем
параграфе используются так называемая
польская запись, которую применял
Лукасевич, и обычная, применяемая в
двузначной логике: отрицание
обозначается через Nx
или ,
конъюнкция - через Кху
или х
v
у,
нестрогая дизъюнкция - через Аху
или х v
у, материальная
импликация - через Сху
или х→
у.
Значение функции от аргумента а
записывается так: [а].
Тавтологией
(или общезначимой, или законом логики,
или тождественно-истинной) называется
формула, которая при любых комбинациях
значений входящих в нее переменных
принимает выделенное (или отмеченное)
значение; как правило, это значение
“истина” (чаще всего в рассматриваемых
системах “истина” обозначается цифрой
1).
,
конъюнкция - через Кху
или х
v
у,
нестрогая дизъюнкция - через Аху
или х v
у, материальная
импликация - через Сху
или х→
у.
Значение функции от аргумента а
записывается так: [а].
Тавтологией
(или общезначимой, или законом логики,
или тождественно-истинной) называется
формула, которая при любых комбинациях
значений входящих в нее переменных
принимает выделенное (или отмеченное)
значение; как правило, это значение
“истина” (чаще всего в рассматриваемых
системах “истина” обозначается цифрой
1).
Развитие многозначных логик подтверждает мысль, что истина всегда конкретна, а также положение об относительном характере конкретно-научных знаний: то, что является тождественно-истинным в одной логической системе, не оказывается тождественно-истинным в другой.
________________
'См.: Доклады АН СССР. 1974. Т. 214, № 1-6; Т. 215, № 1.
417
Трехзначная система Лукасевнча
Трехзначная
пропозициональная логика (логика
высказываний) была построена в 1920 г.
польским математиком и логиком Я.
Лукасевичем (1878-1956)'. В ней “истина”
обозначается 1, “ложь” - 0, “нейтрально”
- 1/2.
 В
качестве основных функций взяты
отрицание (Nx)
и импликация (Сху);
производными являются конъюнкция (Кху)
и дизъюнкция (Аху).
Тавтология принимает значение 1.
В
качестве основных функций взяты
отрицание (Nx)
и импликация (Сху);
производными являются конъюнкция (Кху)
и дизъюнкция (Аху).
Тавтология принимает значение 1.
Отрицание и импликация соответственно определяются матрицами (таблицами) так:
|
Импликация Лукасевича | |||
|
X \ y |
1 |
1/2 |
0 |
|
1 |
1 |
1/2 |
0 |
|
1/2 |
1 |
l |
1/2 |
|
0 |
1 |
l |
1 |
Отрицание Лукасевича
|
х |
Nx |
|
1 |
0 |
|
1/2 |
1/2 |
|
0 |
1 |
[Nx] =1-[x]
'См.: Lukasiewicz J. О pojeciu mozliewosci //Buch Filozoficzny. Lwow. 1920. Vol. 5. № 9.
418
Конъюнкция определяется как минимум значений аргументов: [Кху] = min ( [х],[у]); дизъюнкция - как максимум значений х и у[Аху]=таx ([х],[у]).
Пользование таблицей для импликации Лукасевича, выраженной в форме х → у, происходит так. Слева в первой колонке написаны значений для х, а сверху - значения для у. Возьмем, например [х] = 1/2 (т. е. значение для х, равное 1/2 ), а [у] = 0, получаем импликацию 1/2→ 0. На пересечении получаем результат 1/2 .
Если
в формулу входит одна переменная, как,
например, в случае формулы a , то таблица истинности для этой формулы,
включающая все возможные значения
истинности, или ложности, или
неопределенности ее переменной в
таблице, будет состоять из 3' = 3 строки;
при двух переменных в таблице будет 32
= 9 строк; при
трех переменных в таблице
имеем З3
= 27 строк; при n
переменных будет 3n
строк.
, то таблица истинности для этой формулы,
включающая все возможные значения
истинности, или ложности, или
неопределенности ее переменной в
таблице, будет состоять из 3' = 3 строки;
при двух переменных в таблице будет 32
= 9 строк; при
трех переменных в таблице
имеем З3
= 27 строк; при n
переменных будет 3n
строк.
Покажем, как
происходит доказательство для формул
a (закон
исключенного третьего) и для
(закон
исключенного третьего) и для
 ( закон непротиворечия), содержащих
одну переменную, т. е. а. В таблице будет
всего 3' = 3 строки.
( закон непротиворечия), содержащих
одну переменную, т. е. а. В таблице будет
всего 3' = 3 строки.
|
a |
|
a |
a
^
|
|
|
1 |
0 |
1 |
0 |
1 |
|
1/2 |
1/2 |
1/2 |
1/2 |
1/2 |
|
0 |
1 |
1 |
0 |
1 |
Для
доказательства формулы a используем знание о том, что дизъюнкция
берется по максимуму. В третьей колонке,
соответствующей a,
видим, что вместе со значениями 1 есть
значение 1/2
. Следовательно, эта формула не есть
закон логики. Аналогично строятся
колонки 4 и 5, только соблюдая условие,
что конъюнкция берется по минимуму
значений. Формула
используем знание о том, что дизъюнкция
берется по максимуму. В третьей колонке,
соответствующей a,
видим, что вместе со значениями 1 есть
значение 1/2
. Следовательно, эта формула не есть
закон логики. Аналогично строятся
колонки 4 и 5, только соблюдая условие,
что конъюнкция берется по минимуму
значений. Формула
 также
не является законом логики.
также
не является законом логики.
Теперь
посмотрим, является ли законом логики
формула (х
→ ( ^
у))
→
^
у))
→ ,
содержащая две переменные х
и у
В таблице будет З2
= 9 строк. Распределение значений
истинности для х
и у
показано
в первой и второй колонках.
,
содержащая две переменные х
и у
В таблице будет З2
= 9 строк. Распределение значений
истинности для х
и у
показано
в первой и второй колонках.
419
Вывод: так как в последней колонке встречается два раза значение неопределенности (т. е. 1/2), то данная формула не является законом логики.
На основе данных
определений отрицания, конъюнкции и
дизъюнкции Лукасевича не будут
тавтологиями (законами логики) закон
непротиворечия и закон исключенного
третьего двузначной логики. В системе
Лукасевича не являются тавтологиями и
отрицания законов непротиворечия и
исключенного третьего двузначной
логики. Поэтому логика Лукасевича не
является отрицанием двузначной
логики. В логике Лукасевича тавтологиями
являются: правило снятия двойного
отрицания, все четыре правила де
Моргана и правило контрапозиции: а
→ b

 →
→ .
Не являются тавтологиями правила
приведения к абсурду двузначной логики;(х
→
.
Не являются тавтологиями правила
приведения к абсурду двузначной логики;(х
→
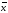 )
→
)
→ и(х→
(
и(х→
( ^
у))
→
^
у))
→
 (т. е. если изх
вытекает противоречие, то из этого
следует отрицание х).
Это было доказано (см. таблицу 3).
(т. е. если изх
вытекает противоречие, то из этого
следует отрицание х).
Это было доказано (см. таблицу 3).
Таблица 3
|
x |
у |
|
|
|
x→( |
(x→
( |
|
1 |
1 |
0 |
0 |
0 |
0 |
1 |
|
1 |
1/2 |
0 |
1/2 |
1/2 |
1/2 |
1/2 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
|
1/2 |
1 |
1/2 |
0 |
0 |
1/2 |
1 |
|
1/2 |
1/2 |
1/2 |
1/2 |
1/2 |
1 |
1/2 |
|
1/2 |
0 |
1/2 |
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
0 |
1/2 |
1 |
1/2 |
1/2 |
1 |
1 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
В системе Лукасевича не являются тавтологиями и некоторые формулы разделительно-категорического силлогизма с нестрогой дизъюнкцией.
Все тавтологии логики Лукасевича являются тавтологиями в двузначной логике, ибо если отбросить значение 1/2, то в логике
420
Лукасевича и в двузначной логике определение функций конъюнкции, дизъюнкции, импликации и отрицания соответственно совпадут. Но так как в логике Лукасевича имеется третье значение истинности –1/2, то не все тавтологии двузначной логики являются тавтологиями в логике Лукасевича.





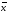

 ^
y
^
y ^y)
^y) ^
у))
→
^
у))
→