РГР (методика)

Расчетно – графическая работа

Построение уравнения регрессии

Цель работы: создание математической функции (модели) наилучшим образом описывающей экспериментальные (табличные, диаграммные) данные, проведение исследования адекватности модели и значимости ее параметров, использование модели для прогнозирования.

Справка

На практике довольно часто приходится сталкиваться с некоторым набором экспериментальных величин, требующих аналитической обработки. Как правило, для этих данных нужно подобрать некоторую модель, которая позволяет описывать наблюдаемые явления и, с некоторой долей вероятности, строить соответствующие прогнозы. В таких случаях математическая формулировка задачи ставится следующим образом. Имеются две наблюдаемые величины х и у, причем у зависит от х некоторым образом. Необходимо построить математическую модель , где f(x) − некоторая функция от х наилучшим образом описывающую наблюдаемые значения у. Обычно следует выбирать так, чтобы минимизировать сумму квадратов разностей (метод наименьших квадратов) между наблюдаемыми и теоретическими значениями зависимой переменной у и , т. е. минимизировать некоторую функцию:

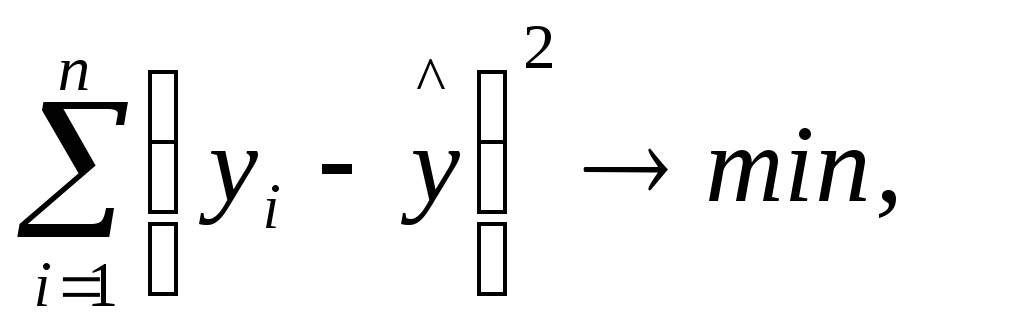
где n − число наблюдений.

При решении такой задачи, главной проблемой является выбор некоторой математической функции, позволяющей достоверно описывать полученные экспериментальные данные и прогнозировать ожидаемые результаты. В MS Excel существует возможность быстрого расчета наиболее подходящей линии, которая проходит через серию заданных точек. Это так называемая линия тренда, по которой можно проследить развитие функции с наименьшей ошибкой. Линия тренда (основное название − линия регрессии) − статистический инструмент, представляющий собой линию , построенную на основе данных диаграммы у с использованием некоторой аппроксимации. В некоторых случаях этими результатами можно воспользоваться для анализа тенденций и краткосрочного прогнозирования. Удобной математической моделью экспериментальных зависимостей является уравнение вида Y(X) = f(X) + , где  − случайная переменная (остатки). Это уравнение называется уравнением регрессии; функция f(X) − функцией регрессии. Относительно случайной величины  обычно делается предположение, что она имеет нормальное распределение с нулевым средним значением. Выбор функции f(X) методом наименьших квадратов составляет задачу регрессионного анализа. Тип функции регрессии в значительной мере зависит от экспериментальных данных, однако наиболее часто используют многочлен вида Y = a + b₁X + b₂X² + … + b_mX^m (коэффициенты a и b_i определяется на основе экспериментальных данных). Такая функция линейной регрессии называется полиномиальной.

В MS Excel для проведения регрессионного анализа используется функция ЛИНЕЙН. Функция ЛИНЕЙН по массивам исходных данных вычисляет коэффициенты b_i и a, а также некоторые статистические характеристики этих коэффициентов и всего уравнения регрессии в целом. Следует отметить, что функция ЛИНЕЙН возвращает массив значений коэффициентов b_i и a (не менее двух значений), поэтому функция должна задаваться в виде формулы массива (с использованием для ввода комбинации клавиш Ctrl+Shift+Enter), в противном случае (при вводе функции в одну ячейку) будет выведено значение только коэффициента b_m.

Синтаксис функции:

={ЛИНЕЙН(известные_значения_У; известные_ значения_Х; 1; 1)}

Для уравнения регрессии = a + bX функция возвращает массив {5 х 2}.

где а − константа регрессионного уравнения, b − коэффициент наклона линии регрессии, Sa − стандартная ошибка коэффициента а, Sb − стандартная ошибка коэффициента b, R² − коэффициент детерминации, Е − стандартная ошибка модели, F − критерий Фишера для проверки значимости регрессии, n−k − степень свободы, SS1 − общая сумма квадратов регрессии, SS2 − сумма квадратов остатков регрессии.

Процесс регрессионного анализа включает в себя следующие этапы: выбор функции регрессии, построение функции регрессии, проверка адекватности функции регрессии, определение статистических характеристик параметров функции регрессии, прогнозирование.

ЗАДАНИЕ 1

С помощью MS Excel провести автоматический анализ тренда на основе диаграммы данных Х и У.

В MS Excel предлагается выбрать тренд из пяти типов аппроксимирующих линий.

Тип	Описание
1. Линейная	Аппроксимирующая прямая: Y = bX + a, где b − тангенс угла наклона, а − точка пересечения прямой с осью Y
2. Логарифмическая	Логарифмическая аппроксимация: Y = b*ln(X) + a, где a и b − константы, ln − натуральный логарифм
3. Полиномиальная	Полиномиальная аппроксимация: Y = b1X6 + b2X5 + b3X4 + b4X3 + b5X2 + b6X + a, где bi, 1,2, … ,6, и а − константа. Максимальная степень полинома 6
4. Степенная	Степенная аппроксимация: Y = b*Xa , где a и b − константы
5. Экспоненциальная	Экспоненциальная аппроксимация: Y = b*eaX, где a и b − константы, е − основание натурального логарифма.

Порядок выполнения задания:

В MS Excel открыть новую книгу и на первом листе ввести данные для X и Y (рис. 1.).

Построить диаграмму данных в виде точечного графика.

Активизировать диаграмму и выполнить команду Диаграмма | Добавить линию тренда … | окно Линия тренда | вкладка Параметры (флаг − показать уравнение на диаграмме; флаг − поместить на диаграмму величину достоверности аппроксимации (R^2)).

Изменяя значения Y проследить за изменениями коэффициента детерминации (R²) и подобрать ту линию регрессии, при которой R² будет максимальным. Обратить внимание на вид уравнения регрессии.

Р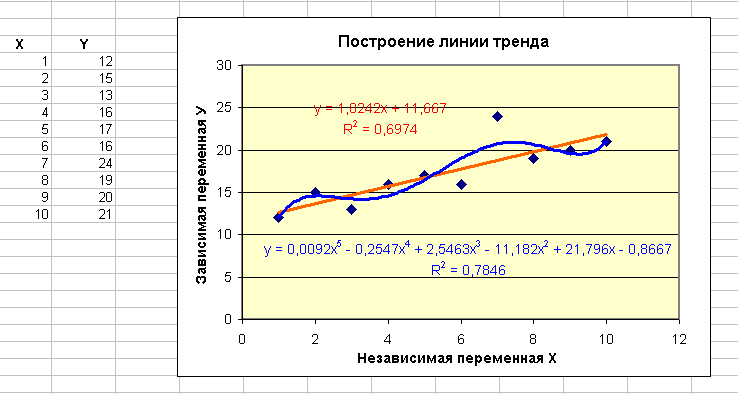 ис. 1.

ЗАДАНИЕ 2

С помощью MS Excel провести регрессионный анализ данных своего варианта. Для чего:

1. провести расчет простого уравнения линейной регрессии;

2. проверить адекватность уравнения регрессии (модели) исходным данным;

3. проверить достоверность коэффициентов модели;

4. провести анализ остатков;

5. применить разработанную модель для прогнозирования.

Все задание размещается на одном рабочем листе. Разработанная модель должна быть наглядной, при изменении исходных данных должен осуществляться пересчет соответствующих величин и перестройка графиков.

П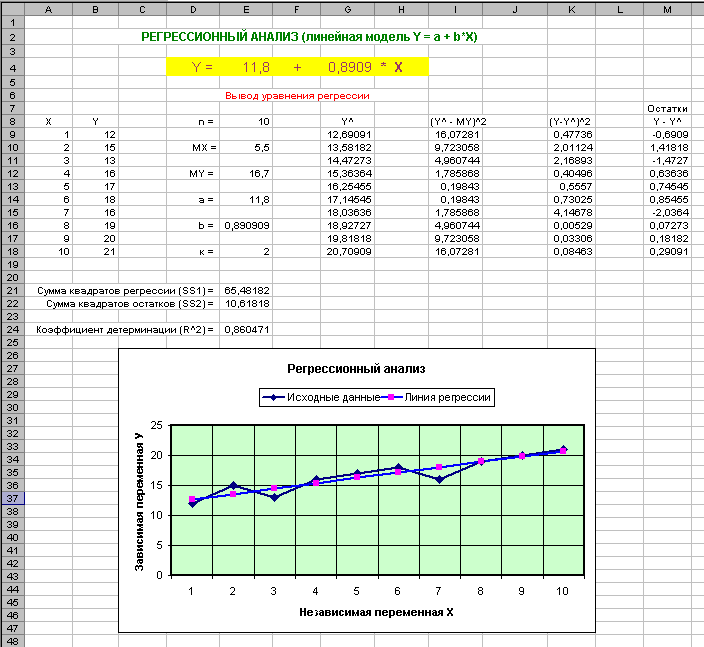 римерный вид модели изображен на рис. 2, 3, 4.

Рис. 2.

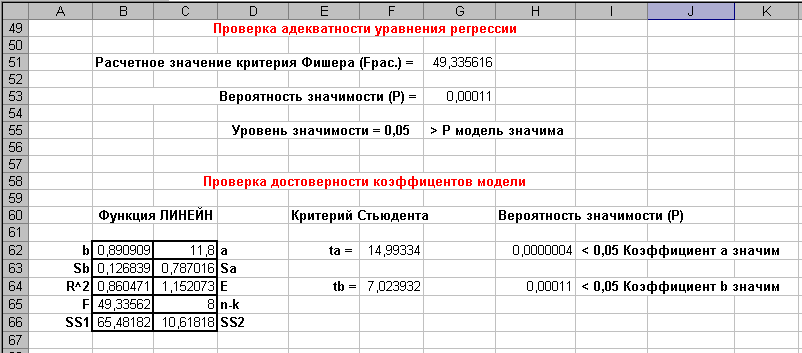
Рис. 3.

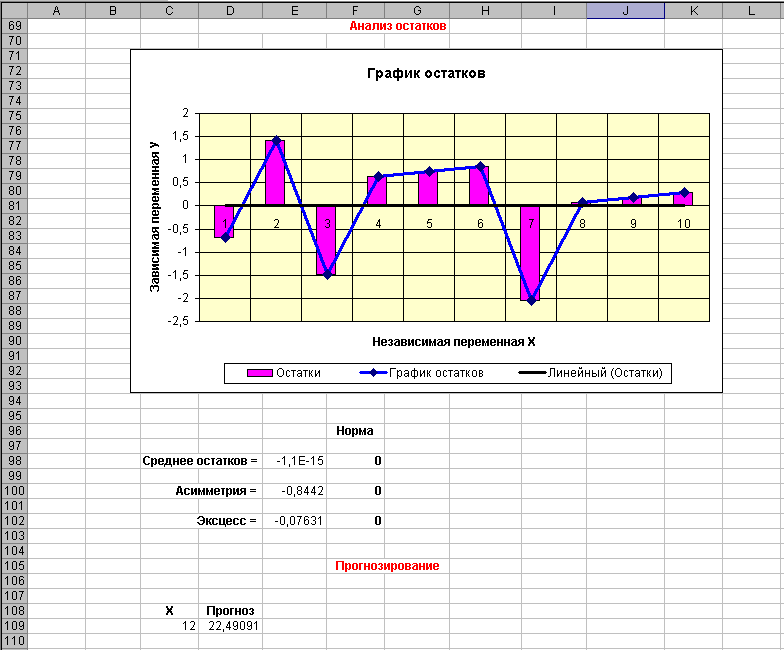
Рис. 4.

Формулы, используемые для построения линейной регрессионной модели

Вывод уравнения регрессии.

Х − независимая переменная,

Y − зависимая переменная,

k − количество определяемых коэффициентов уравнения,

n − =СЧЕТ(Х) − количество элементов в выборке,

МХ − =СРЗНАЧ(Х) − среднее арифметическое переменной Х,

МY − =СРЗНАЧ(Y) − среднее арифметическое переменной Y,

а − =ОТРЕЗОК(Y;X) − коэффициент а,

b − =НАКЛОН(Y;X) − коэффициент b,

Y^ = a + b*X − уравнение регрессии,

SS1 − =СУММ((Y^ − MY)²) − общая сумма квадратов регрессии,

SS2 − =СУММ((Y − Y^)²) − сумма квадратов остатков регрессии,

R² = SS1 / (SS1 + SS2) − коэффициент детерминации,

Y − Y^ − остатки.

Проверка адекватности регрессионного уравнения

F = (SS1*(n − k))/(SS2*(k − 1)) − расчетное значение критерия Фишера,

P =FРАСП(F_рас; k − 1; n − k) − вероятность значимости

Если P < 0,05 то модель значима и годится для использования

Если Р > 0,05 то модель не значима и данные отражает не корректно

Проверка достоверности коэффициентов модели

В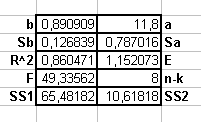ычисляется функция ЛИНЕЙН

{=ЛИНЕЙН(Y;X;1;1)} =

ta = a / Sa − расчетное значение критерия Стьюдента для коэффициента а

tb = b / Sb − расчетное значение критерия Стьюдента для коэффициента b

P_a − =СТЬЮДРАСП(ta; n − k; k) − вероятность значимости коэффициента а,

Р_b − =СТЬЮДРАСП(tb; n − k; k) − вероятность значимости коэффициента b,

ЕСЛИ Р < 0,05 то коэффициент значим.

Анализ остатков

Строится диаграмма Y − Y^ от X в виде гистограммы и графика на одной области построения. С этой целью на первом шаге мастера построения диаграммы нужно выбрать вкладку Нестандартные и выделить позицию График|гистограмма.

Среднее остатков =СРЗНАЧ(Y − Y^) − норма если 0,

Асимметрия =СКОС(Y − Y^) − норма если 0,

Эксцесс =ЭКСЦЕСС(Y − Y^) − норма если 0.

Прогнозирование

Y_{прогноз} = a + b* Х_{прогноз}

Литература

1. Рудикова Л.В. Microsoft Excel для студента. − СПб.: БХВ-Петербург, 2005.

2. Мак-Федрис, Пол. Формулы и функции в Microsoft Excel 2003.: − М.: Издательский дом «Вильямс», 2006.

3. Минько А.А. Статистический анализ в MS Excel. : − М.: Издательский дом «Вильямс», 2004.

8