
- •B15(высокий уровень, время – 10 мин)
- •Пример задания:
- •Ещё пример задания:
- •Ещё пример задания:
- •Ещё пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Ещё пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Еще пример задания:
- •Задачи для тренировки2:
- •42 Http://kpolyakov.Narod.Ru
Еще пример задания:
Сколько различных решений имеет уравнение
((J → K)→(M N L)) ((M N L)→(¬J K)) (M → J) = 1
где J, K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений J, K, L, M и N, при которых выполнено данное равенство. В качестве ответа Вам нужно указать количество таких наборов.
Решение (вариант 1, использование свойств импликации):
перепишем уравнение, используя более простые обозначения операций:
![]()
логическое произведение трех сомножителей равно единице, поэтому каждый из них должен быть тоже равен единице
учитывая, что
 ,и выполняя замены
,и выполняя замены и
и
 ,
получаем
,
получаем
![]() .
.
рассмотрим последнюю импликацию, которая должна быть равна 1:
 ;
по таблице истинности импликации сразу
находим, что возможны три варианта:
;
по таблице истинности импликации сразу
находим, что возможны три варианта:
поскольку все (в том числе и первые две) импликации должны быть равны 1, по таблице истинности импликации сразу определяем, что
 ,
то есть
,
то есть
![]()
в случае «а» последнее уравнение превращается в
 и не имеет решений
и не имеет решенийв случае «б» имеем
 ,
тогда как
,
тогда как
 и
и
 – произвольные; поэтому есть 4 решения,
соответствующие четырем комбинациям
– произвольные; поэтому есть 4 решения,
соответствующие четырем комбинациям
 и
и

в случае «в» получаем
 ,
то есть для
,
то есть для
 есть единственное решение (
есть единственное решение ( ),
а для
),
а для
 – три решения (при
– три решения (при
 ;
; и
и ;
;
 и
и )
)проверяем, что среди решений, полученных в п. 7 и 8 нет одинаковых
таким образом, всего есть 4 + 1 + 3 = 8 решений
ответ – 8
Решение (вариант 2, использование свойств импликации, А.М. Фридлянд, УГАТУ):
перепишем уравнение, используя более простые обозначения операций:
![]()
логическое произведение трех сомножителей равно единице, поэтому каждый из них должен быть тоже равен единице
учитывая, что
 ,и выполняя замены
,и выполняя замены и
и
 ,
получаем
,
получаем
![]() .
.
преобразуем первые две скобки:
 ,
где знак
,
где знак означает операцию «эквивалентность».
Так как это выражение должно быть
истинным, значения
означает операцию «эквивалентность».
Так как это выражение должно быть
истинным, значения
 и
и
 совпадают. Поэтому исходное уравнение
распадается на 2 случая:
совпадают. Поэтому исходное уравнение
распадается на 2 случая:
В случае а) из первого уравнения сразу получаем, что
 .
Тогда третье уравнение справедливо
при любом
.
Тогда третье уравнение справедливо
при любом
 ,
а второе имеет 7 решений (любое, кроме
,
а второе имеет 7 решений (любое, кроме
 ).
).в случае б) из второго уравнения получаем:
 ,
но тогда из третьего уравнения следует,
что
,
но тогда из третьего уравнения следует,
что
 (иначе
(иначе ),
а тогда и
),
а тогда и
 (иначе
(иначе ).
).таким образом, всего есть 7 + 1 = 8 решений
ответ – 8
Решение (вариант 3, декомпозиция, автор идеи – А. Сидоров, ЭПИ МИСИС):
перепишем уравнение, используя более простые обозначения операций:
![]()
идея заключается в том, что мы выбираем одну какую-нибудь переменную и отдельно рассматриваем случаи, когда она равна 0 и 1; такой подход, когда большая задача разбивается на несколько более простых, называют декомпозицией
логическое произведение трех сомножителей равно единице, поэтому каждый из них должен быть тоже равен единице
например, пусть
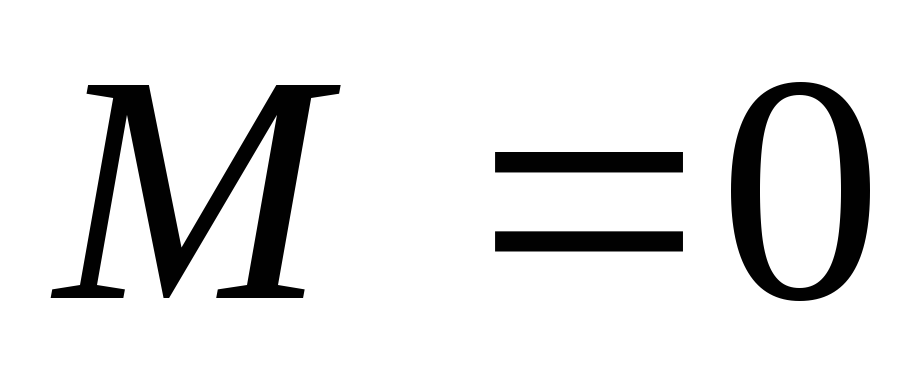 ;
тогда требуется, чтобы
;
тогда требуется, чтобы ,
по таблице истинности импликации
получается, что при этом
,
по таблице истинности импликации
получается, что при этом может быть любое («из лжи следует что
угодно»);
может быть любое («из лжи следует что
угодно»);выполним второй шаг декомпозиции: рассмотрим отдельно варианты
 и
и
при
 и
и получаем
получаем
![]()
это равенство истинно, если
![]() ,
а такого не может быть, то есть в этом
случае решений нет
,
а такого не может быть, то есть в этом
случае решений нет
при
 и
и получаем
получаем
![]()
это равенство истинно только при
![]() (иначе первая скобка равна нулю), но у
нас никак не ограничены значения
(иначе первая скобка равна нулю), но у
нас никак не ограничены значения![]() и
и![]() поэтому получается, что при
поэтому получается, что при![]() и
и![]() есть4 решения(при
есть4 решения(при![]() и всех 4-х различных комбинациях
и всех 4-х различных комбинациях![]() и
и![]() )
)
теперь проверяем вариант, когда
 ;
при этом
;
при этом
![]()
так как должно быть
![]() ,
по таблице истинности операции импликация
сразу получаем
,
по таблице истинности операции импликация
сразу получаем![]() и уравнение преобразуется к виду
и уравнение преобразуется к виду
![]()
выполним второй шаг декомпозиции: рассмотрим отдельно варианты
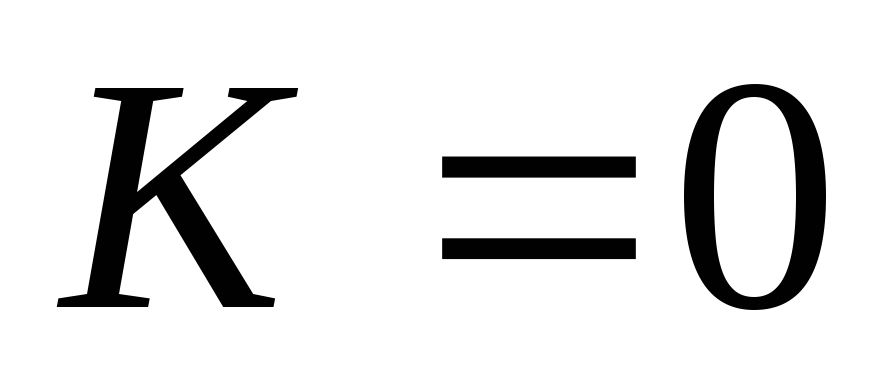 и
и
при
 получаем
получаем ,
откуда сразу следует, что
,
откуда сразу следует, что (3 решения:
(3 решения: ;
; и
и )
)при
 получаем
получаем ,
откуда сразу следует, что
,
откуда сразу следует, что (1 решение:
(1 решение: )
)таким образом, уравнение всего имеет 4+3+1 = 8 решений
ответ – 8
Решение (вариант 4, декомпозиция, автор идеи – А. Сидоров, ЭПИ МИСИС):
та же декомпозиция, но в другом порядке
сделаем сначала декомпозицию по

рассмотрим вариант, когда
 ;
подставляя это значение в уравнение
;
подставляя это значение в уравнение
![]()
получаем
![]()
учитывая, что
 при любом
при любом («из лжи следует все, что угодно»),
находим
(«из лжи следует все, что угодно»),
находим
![]()
отсюда сразу следует, что
 и по таблице истинности операции
импликация определяем, что
и по таблице истинности операции
импликация определяем, что
 ;
учитывая это, получаем
;
учитывая это, получаем
![]()
этого не может быть, потому что первая
скобка равна нулю; поэтому при
![]() решений нет
решений нет
теперь пусть
 ,
тогда
,
тогда и
и
 ,
поэтому остается уравнение
,
поэтому остается уравнение
![]()
выполним декомпозицию по переменной

при
 получаем
получаем
 ,
что верно при условии
,
что верно при условии
 ;
из всех 8-ми комбинаций значений
переменных
;
из всех 8-ми комбинаций значений
переменных
 ,
,
 и
и
 только одна этому условию не удовлетворяет
(
только одна этому условию не удовлетворяет
( ),
поэтому имеем7
решений
),
поэтому имеем7
решенийпри
 получаем
получаем
 ,
что верно при условии
,
что верно при условии
 ;
из 8-ми комбинаций значений переменных
;
из 8-ми комбинаций значений переменных
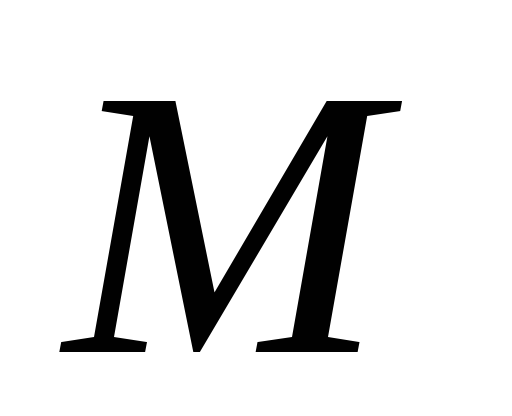 ,
,
 и
и
 только одна (
только одна ( )
удовлетворяет этому условию, поэтому
имеем1 решение
)
удовлетворяет этому условию, поэтому
имеем1 решениетаким образом, уравнение всего имеет 7+1 = 8 решений
ответ – 8
-
Возможные проблемы:
при использовании метода декомпозиции важен порядок выбора переменных для разбиения; можно рекомендовать в первую очередь делать декомпозицию по той переменной, которая чаще всего встречается в уравнении
нужно помнить, что импликация равна нулю только в случае
 ,
часто именно это свойство позволяет
упростить решение
,
часто именно это свойство позволяет
упростить решение
Решение (вариант 5, комбинированный, Т.Н. Наумова, ХМАО, Пыть-Ях, МОУ СОШ №5):
перепишем уравнение, используя более простые обозначения операций:
![]()
имеем логическое произведение трех выражений, которое истинно тогда и только тогда, когда каждое выражение истинно; таким образом, нужно решить систему логических уравнений
![]()
идея состоит в том, чтобы найти все решения одного из уравнений и проверить истинность остальных двух для всех полученных на предыдущем шаге комбинаций значений переменных
рассмотрим первое уравнение:
 ;
оно справедливо в двух случаях:
;
оно справедливо в двух случаях: ,
, –
любое, или
–
любое, или ,
где звездочка означает, что переменная
может принимать значения 0 или 1; всего
получается8 вариантов
,
где звездочка означает, что переменная
может принимать значения 0 или 1; всего
получается8 вариантов ,
, ,
что дает ещётри варианта:
,
что дает ещётри варианта: – два варианта
– два варианта
![]() – один вариант
– один вариант
остается проверить истинность второго (
 )и
третьего (
)и
третьего ( )
равенств для этих 11 вариантов; сразу
видим, что импликация
)
равенств для этих 11 вариантов; сразу
видим, что импликация
 ложна только тогда, когда
ложна только тогда, когда
 ,
то есть для комбинации (10111), а импликация
,
то есть для комбинации (10111), а импликация
 ложна для
ложна для
 при любых значениях остальных переменных:
при любых значениях остальных переменных:J
K
L
M
N

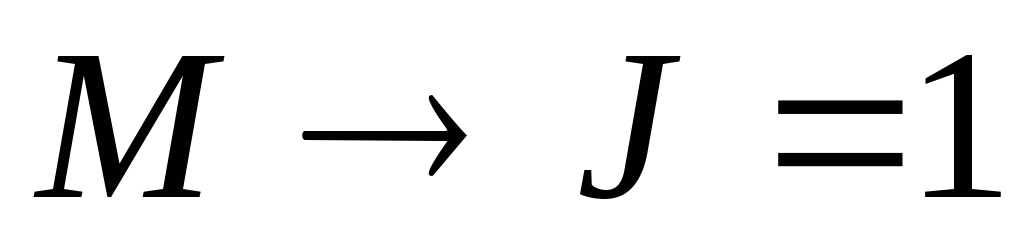
1
0
0
0
0
1
1
1
0
0
0
1
1
1
1
0
0
1
0
1
1
1
0
0
1
1
1
1
1
0
1
0
0
1
1
1
0
1
0
1
1
1
1
0
1
1
0
1
1
1
0
1
1
1
0
1
0
0
1
1
1
1
0
0
1
1
1
1
1
0
1
1
1
1
1
1
1
таким образом, остается 8 вариантов, отмеченных галочками справа от таблицы
ответ – 8


