Метод свертывания

Метод свертывания используется для цепей со смешанным соединением потребителей, то есть, когда есть участки с последовательным и параллельным соединением потребителей.

Расчет цепи со смешанным соединением потребителейпроизводится в следующей последовательности:

• На схеме отмечаются все токи и узловые точки;

• Группы резисторов с явным последовательным или явным параллельным соединением заменяются эквивалентными сопротивлениями;

• Замена соединений эквивалентным сопротивлением производится до получения простейшей схемы;

• По заданному напряжению и эквивалентному сопротивлению находим общий ток;

• Определяем падения напряжения на участках и токи на этих участках;

(привести пример)

Метод преобразования схем

Метод преобразования схем применяют для расчета сложных цепей, в которых невозможно использовать метод свертывания без дополнительных преобразований, так как там присутствуют соединения типа «треугольник» или «звезда». Соединение «треугольник» преобразуют в соединение «звезда» или, наоборот, для того, чтобы потом цепь можно было легко свернуть. Эти преобразования проводятся при условии, что электрические параметры (ее баланс) не нарушаются.

Если есть соединение «треугольник» с узлами А, В, Си сопротивлениямиR_{АВ ,}R_{ВС ,}R_СА, то его можно преобразовать в соединение «звезда» с общим узломОи сопротивлениями на участках:

АО – R_A;

BO – R_B;

CO – R_C.

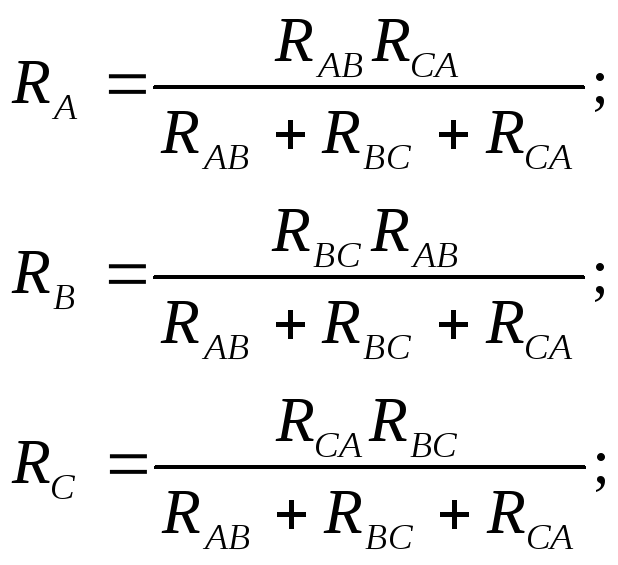
Для того, чтобы преобразовать соединение «звезда» с общим узлом Ои сопротивлениями на участках:АО – R_A; BO – R_B;CO – R_C. в соединение «треугольник» с узламиА, В, Си сопротивлениямиR_{АВ ,}R_{ВС ,}R_СА , необходимо рассчитать сопротивления «треугольника» по заданным сопротивлениям «звезды», воспользовавшись следующими соотношениями:

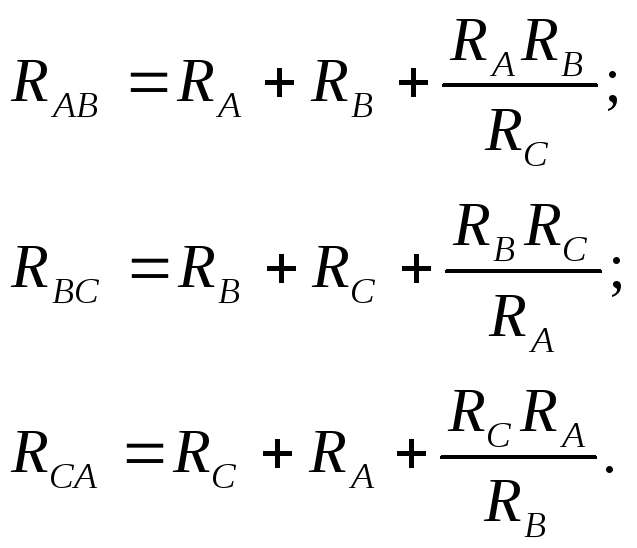
Метод наложения

Метод наложения используется для расчета сложных электрических цепей, имеющих несколько источников.

Порядок расчета:

• В каждой ветви выбираем и показываем на чертеже произвольно направление токов;

• Количество расчетных схем в цепи равно количеству источников в исходной схеме;

• В каждой расчетной схеме действует только один источник, а остальные заменяются их эквивалентным сопротивлением;

• В каждой расчетной схеме методами преобразования и сворачивания находятся частичные токи. Частичным называется ток, протекающий в ветви под действием только одного источника;

• Искомые токи в ветвях находятся как алгебраическая сумма частичных токов в этих ветвях.

Метод узлового напряжения

Расчет сложной электрической цепи с несколькими источниками можно произвести с помощью метода узлового напряжения.

Порядок расчета цепи:

• Произвольно в ветвях выбираем и показываем на схеме направления токов;

• Выбираем базисный узел (φ=0В) и выбираем положительные направления узловых напряжений от независимых узлов к базисному узлу;

• Определяем узловые токи, узловые и общие проводимости. При этом токи источников, направленные к узлам, принимают положительными;

• Для определения токов в ветвях составляют систему уравнений по первому закону Кирхгофа для узла.

Узловой проводимостью называют сумму проводимостей всех ветвей, присоединенных к данному узлу.

Общей проводимостью называется сумма проводимостей всех ветвей, соединяющих данные два узла.