2. Магнитный поток. Теорема Гаусса для магнитного потока.

Потоком вектора (магнитным потоком) через площадку dS называется скалярная величина, равная

где - проекция на направление нормали к площадке;

 - угол между векторами и .

- направленный элемент поверхности,

Поток вектора - алгебраическая величина,

если - при выходе из поверхности;

если - при входе в поверхность.

Поток вектора магнитной индукции через произвольную поверхность S равен

Для однородного магнитного поля =const,

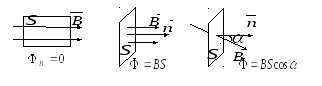
1 Вб - магнитный поток, проходящий через плоскую поверхность площадью 1 м², расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл.

Магнитный поток через поверхность S численно равен количеству магнитных силовых линий, пересекающих данную поверхность.

Поскольку линии магнитной индукции всегда замкнуты, для замкнутой поверхности число линий, входящих в поверхность (Ф<0) равно числу линий, выходящих из нее (Ф >0), следовательно, полный поток магнитной индукции через замкнутую поверхность равен нулю.

- теорема Гаусса: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.

Эта теорема является математическим выражением того, что в природе отсутствуют магнитные заряды, на которых начинались бы или заканчивались линии магнитной индукции.

3. Закон Био-Савара-Лапласа и его применение для расчета магнитных полей.

Магнитное поле постоянных токов различной формы было подробно исследовано фр. учеными Био и Саваром. Ими было установлено, что во всех случаях магнитная индукция в произвольной точке пропорциональна силе тока, зависит от формы, размеров проводника, расположения этой точки по отношению к проводнику и от среды.

Результаты этих опытов были обобщены фр. математиком Лапласом, который учел векторный характер магнитной индукции и высказал гипотезу о том, что индукция в каждой точке представляет собой, согласно принципу суперпозиции, векторную сумму индукций элементарных магнитных полей, создаваемых каждым участком этого проводника.

или .

Лапласом в 1820 г. был сформулирован закон, который получил название закона Био-Савара-Лапласа: каждый элемент проводника с током создает магнитное поле, вектор индукции которого в некоторой произвольной точке К определяется по формуле:

- закон Био-Савара-Лапласа.

Из закона Био-Совара-Лапласа следует, что направление вектора совпадает с направлением векторного произведения . Такое же направление дает и правило правого винта (буравчика).

Учитывая, что ,

- элемент проводника, сонаправленный с током;

- радиус-вектор, соединяющий c точкой K;

• - угол между и .

Закон Био-Савара-Лапласа имеет практическое значение, т.к. позволяет найти в заданной точке пространства индукцию магнитного поля тока, текущего по проводнику конечный размеров и произвольной формы.

Для тока произвольной формы подобный расчет представляет собой сложную математическую задачу. Однако, если распределение тока имеет определенную симметрию, то применение принципа суперпозиции совместно с законом Био-Савара-Лапласа дает возможность относительно просто рассчитать конкретные магнитные поля.

Рассмотрим некоторые примеры.

А. Магнитное поле прямолинейного проводника с током.

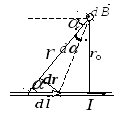
1. для проводника конечной длины:

2. для проводника бесконечной длины: ₁ = 0, ₂ = 

.

Б. Магнитное поле в центре кругового тока:

=90⁰, sin=1,