Лекция 9. Распределения Максвелла и Больцмана. Явления переноса

[1] гл.8, §43-48

План лекции:

1. Закон Максвелла о распределении молекул по скоростям. Характерные скорости молекул.

2. Распределение Больцмана.

3. Средняя длина свободного пробега молекул.

4. Явления переноса:

а).диффузия;

б).внутреннее трение (вязкость);

в).теплопроводность.

1. Закон Максвелла о распределении молекул по скоростям. Характерные скорости молекул.

Молекулы газа движутся хаотически и в результате столкновений скорости их меняются по величине и направлению в газе имеются молекулы как с очень большими, так и с очень малыми скоростями. Можно поставить вопрос о числе молекул, скорости которых лежат в интервале от и для газа в состоянии термодинамического равновесия в отсутствии внешних силовых полей. В этом случае устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям , которое подчиняется статистическому закону , теоретически выведенному Максвеллом.

Чем больше общее число молекул N, тем большее число молекул N будет обладать скоростями в интервале от и ;чем больше интервал скоростей , тем у большего числа молекул значение скоростей будет лежать в указанном интервале.

~

Введем коэффициент пропорциональности f(.

, 

где f( называется функцией распределения, которая зависит от скорости молекул и характеризует распределение молекул по скоростям.

Если вид функции известен, можно найти число молекул , скорости которых лежат в интервале от до .

С помощью методов теории вероятности и законов статистики Максвелл в 1860г. теоретически получил формулу, определяющую число молекул , обладающих скоростями в интервале от до .

, (2)

- распределение Максвелла показывает, какая доля общего числа молекул данного газа обладает скоростями в интервале от до .

Из уравнений  и  следует вид функции 

- (3)

функция распределения молекул идеального газа по скоростям.

Из (3) видно, что конкретный вид функции зависит от рода газа (от массы молекулы m₀) и температуры.

Наиболее часто закон распределения молекул по скоростям записывают в виде:

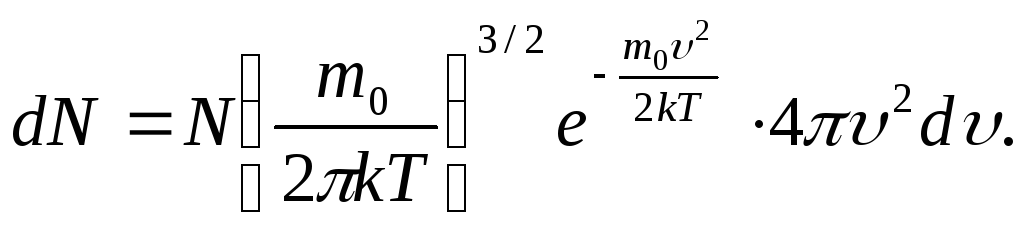
График функции асимметричен (рис. 1). Положение максимума характеризует наиболее часто встречающуюся скорость, которая называется наиболее вероятной. Скорости, превышающие _в, встречаются чаще, чем меньшие скорости.

- доля общего числа молекул, обладающих скоростями в этом интервале.

S_общ.= 1.

С повышением температуры максимум распределения сдвигается в сторону больших скоростей, а кривая становится более пологой, однако площадь под кривой не изменяется, т.к. S_общ.= 1.

Наиболее вероятной называют скорость, близкой к которой оказываются скорости большинства молекул данного газа.

Для её определения исследуем на максимум.

, 4,

, .

, .

Ранее было показано, что

, ,

 .

В МКТ используют также понятие средней арифметической скорости поступательного движения молекул идеального газа.

- равна отношению суммы модулей скоростей всех молекул к

числу молекул.

.

Из сравнения видно (рис.2), что наименьшей является _в.