§ 3. Общезначимость и выполнимость формул. Предваренная нормальная форма (п.Н.Ф.)

Определение 1. Формула логики предикатов назы­вается выполнимой в области М, если существуют зна­чения переменных, входящих в эту формулу и отнесен­ных к области М, при которых формула принимает ис­тинные значения.

Определение 2. Формула А называется выполнимой, если существует область, на которой эта формула вы­полнима.

Определение 3. Формула логики предикатов называ­ется тождественно истинной в области М, если она при­нимает истинные значения для всех значений переменных, входящих в эту формулу и отнесенных к этой области.

Определение 4. Формула А называется общезначи­мой, если она тождественно истинная во всякой области.

Определение 5. Формула А называется тождествен­но ложной в области М, если она принимает ложные значения для всех значений переменных, входящих в эту формулу и отнесенных к этой области.

Из приведенных определений следует:

1. Если формула общезначима, то она и выполнима на всякой области.

2. Если формула тождественно истинна в области, то она выполнима в этой области.

3. Если формула невыполнима, то она тождественно ложна в любой области.

Пример 1. Доказать, что формула

выполнима.

Решение. Для доказательства выполнимости форму­лы А достаточно найти область определения двухместно­го предиката Р(х,у) и такое его значение, что в этой области формула принимает истинные значения. Такой областью определения предиката, в частности, будет мно­жество M = N×N. Действительно, если Р(х,у) — преди­кат , то формула А тождественно истинна в обла­сти М, и, следовательно, выполнима в этой области. Од­нако, если в качестве предиката Р(х,у) взять предикат «у<х», то формула А будет тождественно ложной в области М, и, следовательно, невыполнимой в области М. При этом ясно, что формула А не общезначима.

Пример 2. Доказать, что формула является общезначимой.

Решение. Считая, что формула А определена на лю­бой области М, проведем равносильные преобразования:

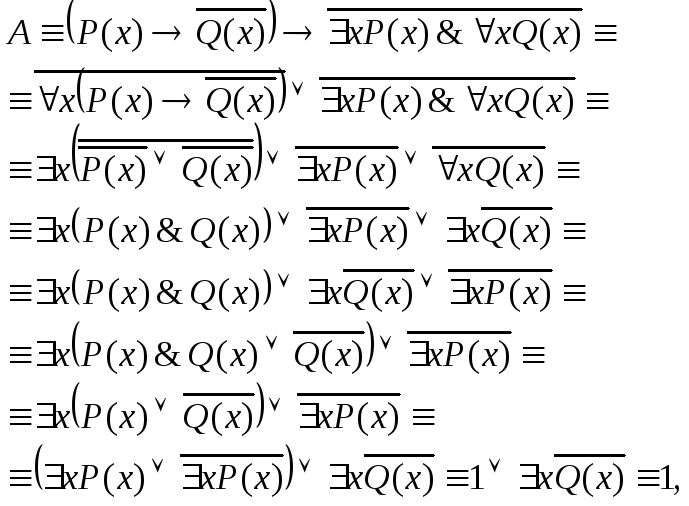
т.е. формула А тождественно истинна для любых одно­местных предикатов Р(х) и Q(х) и в любой области.

Пример 3.

Доказать, что формула

тождественно ложна.

Решение.

Так как формула , а формула , очевидно, тож­дественно ложна, то тождественно ложна и формулаА.

Говорят, что формула логики предикатов имеет нор­мальную форму, если она содержит только операции конъ­юнкции, дизъюнкции и кванторные операции, а опера­ция отрицания отнесена к элементарным формулам.

Среди нормальных форм формул логики предикатов важное значение имеют так называемые предваренные нормальные формы. В них кванторные операции либо полностью отсутствуют, либо используются после всех операций алгебры логики.

Справедливо утверждение о том, что всякая форму­ла логики предикатов путем равносильных преобразова­ний может быть приведена к предваренной нормальной форме (п.н.ф.). При этом следует использовать равно­сильности логики предикатов, которые позволяют вы­носить за скобки кванторы существования и всеобщнос­ти, т.е. равносильности:

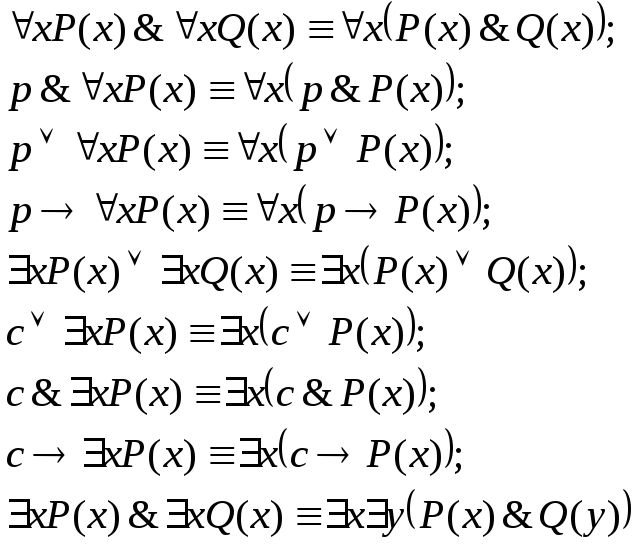
Пример 4.

Привести к п.н.ф. формулу .

Решение. Проводя равносильные преобразования, получим:

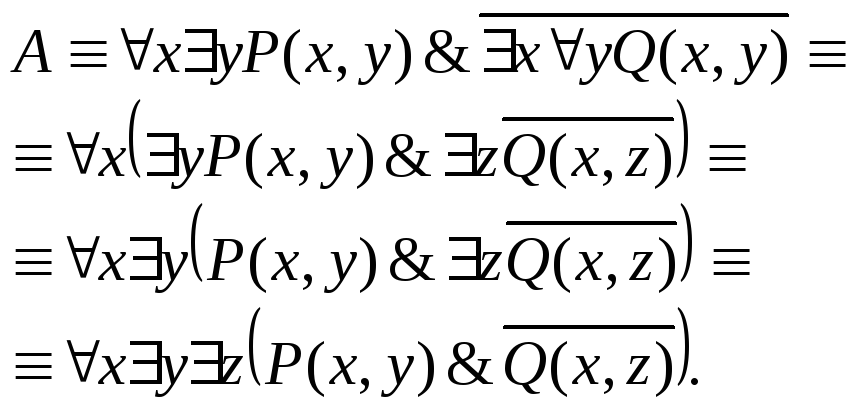
3.28. Выполнимы ли следующие формулы: 1); 2).

3.29. Можно ли привести пример формулы А(х) такой, что выполнима формула:

1) ; 2).

3.30. Доказать, что формула является общезначимой.

3.31. Какие из нижеприведенных формул являются общезначимыми:

3.32. Доказать тождественную ложность формулы 3.33. Привести к п.н.ф. следующие формулы логики предикатов: